
Un pezzo istruttivo sulla programmazione lineare. E' uno strumento utile e facile da usare. Consiglio di dare un'occhiata senza timidità - c'è una buona probabilità che si capisca tutto e che torni utile prima o poi. L'articoletto comincia con un riferimento letterario a un romanzo di Natalia Ginsburg - secondo il quale la prog.lineare era cara ad Adriano Olivetti (che mi pare fosse cognato della Ginsburg).
Citando un umorista degli anni Trenta (sul "Bertoldo"): "Studia la programmasione lineare se vuoi riuscire nel numerico!"
Il giovane era un innovatore vulcanico. Aveva modernizzato l’industria di famiglia puntando su qualità e design. L’azienda era cresciuta molto. Il suo nuovo stile aveva permeato anche l’architettura, i servizi sociali, la cultura d’azienda. Era il personaggio di un romanzo di Natalia Ginsburg: “Le voci della sera” e sembrava ispirato alla figura romanzesca di Adriano Olivetti. Quel presidente-innovatore si era anche appassionato della programmazione lineare e me ne parlava spessissimo. Su questo, però, la scrittrice diceva poco. Si limitava a qualche vaga similitudine. È un peccato perché si tratta di uno strumento utile e abbastanza facile da capire. Lo racconto qui di seguito. Ci vuole un po’ di pazienza e di conoscenza dell’algebra (anche di geometria analitica elementare), ma ne vale la pena. È uno strumento che può risultare utile nei settori e nei mestieri più disparati.
La programmazione lineare è una procedura usata per massimizzare o minimizzare una funzione di primo grado (lineare), come ad esempio un polinomio, di certe variabili che non possono prendere valori negativi e che devono soddisfare un certo insieme di diseguaglianze. Qui mi limito a darne un semplice esempio.
Supponiamo che una fabbrica produca ogni giorno due prodotti X e Y. Ogni pezzo di X dà un profitto di 200 €. Ogni Y dà un profitto di 500 €. Il numero di pezzi X (chiamato x) non può superare 400 unità al giorno.
Il numero di pezzi Y (chiamato y) non può superare 500 unità al giorno. In totale non si possono produrre più di 700 pezzi al giorno (fra X e Y). Dunque vogliamo massimizzare la funzione lineare che rappresenta il profitto totale
P = 200 x + 500 y
con i vincoli
(x + y) <= 700, x <= 400, y <= 500 Il problema può essere affrontato graficamente come nel diagramma a pagina seguente. Le limitazioni citate indicano che le coppie di valori x e y ammesse definiscono un punto nel piano x, y contenuto entro il poligono 0ABCD. I punti devono essere contenuti nel primo quadrante perchè x e y devono essere positivi (non possiamo produrre numeri negativi di unità). Devono essere al disotto della retta orizzontale y = 500 , a sinistra della retta verticale x = 400 e sotto la retta x + y = 700 che è inclinata a 45° e unisce i punti (0, 700) e (700, 0) Se il profitto è zero, P = 0 la funzione lineare scritta sopra è rappresentata dalla retta di equazione 200 x + 500 y = 0
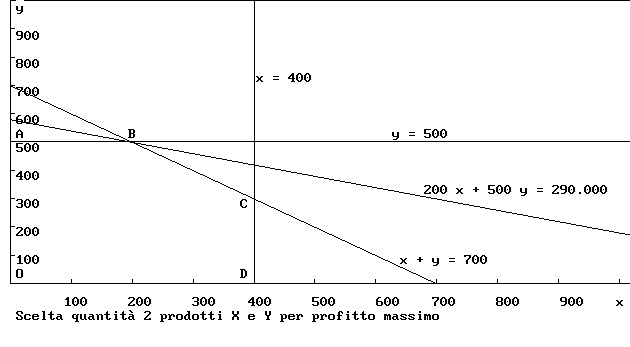
Per valori positivi di P tutte le rette di equazione P = 200 x + 500 y sono parallele a quella per P = 0 e site più in alto di essa.
Allora la soluzione del problema si trova spostando parallelamente a se stessa la retta 200 x + 500 y = 0 fino a trovare la posizione più lontana da quella originale e che contenga almeno un punto del poligono nero. È ovvio dal diagramma che il punto cercato è l' intersezione B fra le rette
y = 500 e (x + y) = 700,
le cui coordinate sono (200, 500).
È facile vedere che la parallela alla retta 200 x + 500 y = 0 che passa per il punto B (200, 500) ha equazione:
200 x + 500 y = 200 . 200 + 500 . 500 = 40.000 + 250.000 = 290.000 €
ed è rappresentata in figura. Questo risolve il problema. Ogni giorno la fabbrica deve produrre 200 X e 500 Y, ottenendo così il massimo profitto possibile di 290.000 €.
Facciamo un semplice controllo. Se producessimo di nuovo 700 pezzi in tutto: ma suddivisi in 400 X e 300 Y, il punto rappresentativo di questa scelta è C (400, 300) e il profitto corrispondente sarebbe
200 x + 500 y = 200 . 400 + 500 . 300 = 80.000 + 150.000 = 230.000 €
inferiore al massimo calcolato sopra.
Naturalmente la programmazione lineare comprende strumenti e obiettivi ben più vasti del modesto esempio presentato qui. Una teoria più completa, con esempi, si trova facilmente cercando su Google: “programmazione lineare” (in inglese “linear programming”).
Main image: Leonid Kantorivich | Via Wikipedia








Leonid Kantorivich,
il primo in assoluto a sviluppare la programmazione lineare (durante la seconda guerra mondiale).
Un altro grande personaggio poco conosciuto.
Alcuni problemi di programmazione lineare con svolgimento sul blog dei nostri studenti di quinta informatica