La precisione con la quale siamo in grado di convertire un dato analogico in uno digitale è limitata da diversi fattori ed è importante valutarli, pesarli, stimarli opportunamente prima di iniziare a prototipare il progetto del circuito. Vediamo, quindi, alcuni dei contributi di errore più frequenti e quanto incidono proprio sulla risoluzione effettiva.
Quest'oggi ci occupiamo di sistemi che effettuano la conversione tra digitale ed analogico. Quando decidiamo quali sono le specifiche di un sistema DAC stiamo, innanzitutto, decidendo quale sia il valore di tensione di riferimento di lavoro e sappiamo bene che questo va di pari passo con le performance del sistema. La scelta del DAC e dei riferimenti non può che esser fatta di conseguenza. Le specifiche tecniche del componente, ovvero le sue caratteristiche, possono essere studiate per garantire al sistema il soddisfacimento dei requisiti al costo più basso.
Ci occupiamo, in particolare, oggi del DAC della Maxim a tre terminali; per progettare un sistema è, prima di tutto, necessario capire come specificare il funzionamento di tutte le sue parti e come le caratteristiche interagiscano tra loro. Nell'error budget analysis, in particolare, questo principio si “amplifica” poiché gli errori si propagano attraverso il sistema, come vedremo.
Caratteristiche del riferimento di tensione
Voltage Reference
La precisione iniziale rappresenta la “tolleranza” sull'uscita in tensione, senza tenere conto degli effetti della temperatura, della tensione in ingresso oppure del carico. Le condizioni di test prevedono una temperatura di 25 °C (temperatura ambiente).
Il riferimento di tensione in uscita può subire dei cambiamenti che vengono misurati ad una data temperatura; questi vengono indicati in ppm/°C. La Maxim utilizza il “box method”. La “forma” dei cambiamenti in dipendenza dalla temperatura non è specificata, ovvero non abbiamo a che fare con una funzione matematica precisa. Ciò che, però, è specificato chiaramente sono i limiti della variazione in oggetto, anche se questi non coincidono necessariamente con i limiti della temperatura.
Pertanto, per calcolare il massimo scostamento è necessario moltiplicare il coefficiente di temperatura per il range di temperature del singolo componente. Con questo metodo si calcola, ad esempio, che, per un pezzo che dimostri un coefficiente di temperatura di 5ppm/°C, in un intervallo che va da -40°C fino a +85°C, la massima deriva dovuta alla temperatura viene calcolata come:
ΔV = (TMAX - TMIN) × TC = (85 + 40) × ±5 = ±625ppm
in linea di principio è molto meglio selezionare dispositivi che abbiano variazioni di valore all'interno del range, piuttosto che fuori o ai limiti.
Un esempio è il MAX6025A, per il quale si indica un valore di 15 ppm/°C riferito ad un intervallo che vada 0 °C fino a 70 °C.
Questi valori di riferimento sono validi fino a 1050ppm. Ad ogni modo, se si sceglie un riferimento di valore pari a 1050, specificato in un intervallo di temperatura che va da -40 °C fino a +85 °C, si ottiene 1050/125= 8.4 ppm/°C. Alcuni dispositivi sono, comunque, caratterizzati per diversi intervalli di temperatura.
Un esempio grafico di come questo metodo funzioni è riportato nella figura che segue
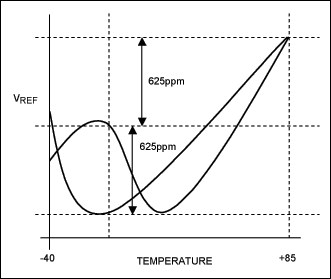
due curve di riferimento vengono mostrate a scopo esemplificativo; esse sono entrambe riferite ad un valore di 5 ppm/°C.
In generale, non è possibile mettere in relazione la variazione di tensione e la temperatura per calcolare la deriva in un intervallo specifico ma piuttosto si cerca di identificare l'entità della deriva di un singolo pezzo, quando si ha a che fare con un sistema complesso.
Regolazione di linea
Questo termine viene utilizzato per definire la variazione incrementale della tensione in uscita come effetto di una variazione dell'ingresso; viene, di solito, misurata in µV/V. Di fatto, quindi, si tratta di una variazione percentuale che descrive escursioni molto piccole.
Regolazione di carico
in questo caso, facciamo riferimento alla variazione incrementarle della tensione di uscita come effetto della variazione della corrente che fluisce all'interno del carico. Alcuni DAC potrebbero non prevedere
l'uso di un buffer per essere riferiti all'ingresso. Quindi, quando il codice cambia, l'impedenza d'ingresso cambierà coerentemente causando una variazione nella tensione di riferimento. Queste variazioni risultano di gran lunga più importanti quando ci riferiamo a strutture che utilizzano topologie circuitali di stringhe resistive, come strutture R-2R “ladder”.
Isteresi da temperatura
Quando utilizziamo la parola isteresi ci riferiamo sempre ad effetti non lineari ed anche difficili da ripetersi, a parità di condizioni. In questo caso, parliamo di variazioni nella tensione di riferimento alla temperatura di 25 °C dopo che essa è stata fatta variare in un intervallo temporale che va da Tmin a TMAX. Viene specificato un rapporto tra le due tensioni, espresso in ppm, pari a:
TEMPHYST = 106 × (ΔVREF/VREF)
In questo caso, ΔVREF rappresenta la variazione della tensione dovuta proprio alla variazione ciclica della temperatura.
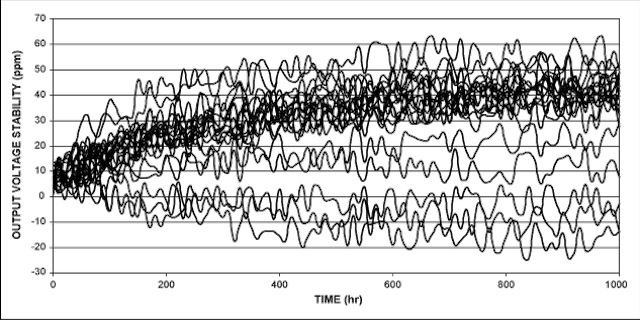
Stabilità sul lungo periodo
La "long-term stability" rappresenta la variazione della tensione d'uscita nel tempo e viene misurata in ppm/1000 ore. La deriva, vista da un punto di vista “cumulativo” su un intervallo di tempo di 1000 ore, non viene generalmente specificata ma risulta molto più bassa rispetto a quella iniziale.
Tensione di rumore d'uscita
Questa figura di merito definisce la tensione di rumore rispetto al riferimento dell'uscita. La componente 1/f viene specificata in µVP-P su una banda che va da 0.1Hz a 10Hz mentre la componente a larga banda viene generalmente misurata come potenza di rumore, misurata in µVRMS su una banda compresa tra 10Hz e 10kHz.
Specifiche tecniche dei DAC
Esistono configurazioni DAC in cui l'uscita è in corrente che vengono tipicamente impiegate in configurazioni note con il nome di MDAC, che servono a fornire un guadagno variabile. Generalmente queste richiedono amplificatori operazionali esterni per fare da buffer per la tensione generata da un resistore.
Qui, invece, ci focalizziamo su quelli che hanno uscita in tensione.
La loro caratteristica principale è la variabilità della resistenza di ingresso del riferimento rispetto al codice. Molte configurazioni DAC vengono implementate utilizzando lo schema R-2R. La resistenza della “scala” cambierà in funzione del codice DAC; pertanto è necessario prestare attenzione per garantire che il riferimento di tensione possa fornire una corrente sufficiente anche alla resistenza che “rappresenta” il minimo valore di riferimento.
Errore in uscita e specifiche sull'accuratezza
L'errore in uscita viene definito come la variazione, rispetto al valore d'uscita ideale, che si verificherà per via dell'imperfetto matching tra la tensione di riferimento ed il DAC. È importante notare che questa particolare figura di merito fa riferimento alla precisione assoluta, nel senso che tutto viene riferito all'intervallo di tensioni d'uscita ideali per un DAC. Se facciamo riferimento, ad esempio, ad un DAC a 12 bit, il codice 4095 dovrebbe produrre una tensione d'uscita pari a 4.096V. Rispetto a questo valore, dunque, ogni altro risulta errato. A questa grandezza, però, si fa riferimento in termini relativi, ovvero definendo l'output full-scale, piuttosto che in termini assoluti.
L'errore in uscita viene spesso specificato come valore one-sided, misurato in LSB e, quindi, come funzione della risoluzione del convertitore ma, in realtà, esso ha almeno due componenti.
Ad esempio, sempre riferendoci al DAC nominato in precedenza, cioè al valore di 4.096 , idealmente, un LSB produce una variazione tipo 4.096V/4095 ~1mV. Se l'errore in uscita specificato in questo caso è pari a 4 LSB con una risoluzione di 12 bit, questo vuol dire che il DAC in uscita, per ciascun codice restituito, può, realmente, fornire un valore che ha una variabilità di ±4 LSBs (o ±4mV).
In generale possiamo scrivere che:
accuratezza = risoluzione del DAC – log2(Errore)
Da questa formulazione, generale, si ottiene che, nell'esempio specifico:
accuratezza = 12 - log2(4) = 10 bits
Pertanto, in realtà, il massimo che si possa ottenere entro 1 LSB è una risoluzione di 10 bit.
Errore di guadagno
Le sorgenti di errore di guadagno principali sono molto diverse tra loro; tra le altre ci sono: coefficiente di temperatura (con effetto sul riferimento in uscita), isteresi sul riferimento dovuto alla temperatura, stabilità del riferimento, regolazione del carico, rumore sull'uscita, errore di guadagno del DAC, errore di offset del DAC e poi l'immancabile errore di non linearità integrale (INL).
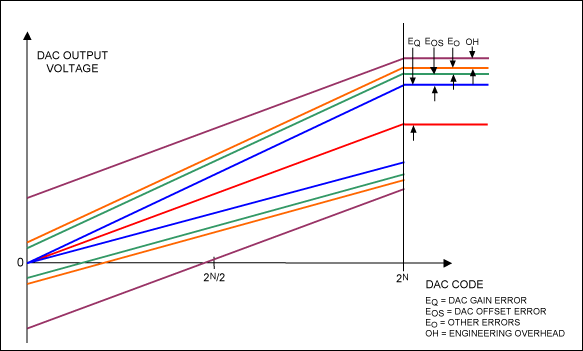
Anche se l'errore si “applica” all'intera scala dei valori del DAC, la maggior parte delle sorgenti di rumore citate in precedenza ha, come effetto, una variazione dell'errore di guadagno che diventa più grande quando ci si avvicina al fondo scala, ovvero per valori più grandi (in modulo). Gli errori di guadagno vanno, però, incontro a riduzione con i valori dei codici restituiti dal DAC. Siccome la relazione di cui stiamo parlando dimostra dipendenza quasi proporzionale ai valori assunti, si capisce che l'errore sparisce del tutto quando la misura è proprio zero. In realtà, questo non è vero perché gli errori di non linearità, quella integrale ma anche quella differenziale, affliggono la misura in maniera costante lungo tutta la scala e per tutti i valori che il convertitore restituisce.
Inoltre, a questi errori ed a questi contributi, si aggiunge il rumore.
L'errore di non linearità integrale viene definito, tipicamente, utilizzando uno dei due metodi possibili: la linearità assoluta oppure il metodo end-point. L'errore di offset viene azzerato e l'errore di guadagno, invece, normalizzato prima di effettuare la misura dell'INL.
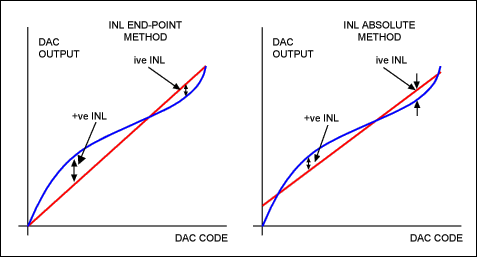
Il primo dei due metodi possibili prevede la comparazione della caratteristica effettiva del convertitore con la caratteristica di funzionamento ideale del dispositivo.
Il secondo metodo, invece, utilizza il fitting con due valori, tutti e due a fondo scala ma coprendo i due estremi distinti. Come mostra la figura, si effettua una comparazione diretta tra la retta che congiunge i due punti che coprono l'intera gamma di valori “restituibili” da parte del convertitore calcolando il maggior distacco della caratteristica reale rispetto ad essa.
Se vogliamo, il secondo metodo risulta più rappresentativo del caso peggiore, ovvero della più grande distanza che il dato reale o dimostrare quello quantizzato.
Tuttavia, non è possibile definire quale dei due metodi sia in assoluto il migliore; la scelta tra l'uno e l'altro dovrà essere effettuata iin funzione della specifica applicazione.
A questo punto, in conclusione ed a scopo illustrativo, proponiamo una tabella riassuntiva delle proprietà già elencate con alcuni valori tipici, in funzione dello specifico esempio di progetto di riferimento.









spiegazione esaustiva! complimenti!
Grazie Ionela ma… non è ancora finita 🙂
Faccio un’anticipazione, dovuta peraltro: quei 4 schemi (o tipi) di progetto che si trovano in tabella vanno molto accuratamente analizzati e questo, ho capito, necessitava di esser fatto in maniera completa…. in una fase successiva… 🙂
Ecco, infatti, quello cui facevo riferimento: http://it.emcelettronica.com/4…
Buona lettura 🙂