La legge di Benford è una bizzarra legge statistica, molto utile per scoprire se qualcuno abbia falsificato dei dati. Vediamo come usarla al meglio, anche per le nostre applicazioni pratiche di tutti i giorni.
Anche quando le informazioni e i dati sembrano profondamente irregolari e non legate tra loro da alcun vincolo, c'è sempre un nesso logico o matematico che ci mette lo zampino. E' il caso della legge di Benford che, benché non sia una esatta formula matematica ma statistica, regala spesso la sua validità nei campi più disparati della vita pratica e quotidiana.
La legge di Benford descrive la probabilità che ha una cifra numerica di essere presente nella parte iniziale di una raccolta di dati reali. In altre parole, descrive la probabilità che un dato numerico, appartenente ad una collezione di dati reali, inizi con una determinata cifra numerica (da 1 a 9).
Ancora, essa permette di controllare, con un certo grado di affidabilità, se un elenco di dati è genuino e originale oppure è stato del tutto inventato o alterato in parte.
Secondo questa legge, in una grande quantità di dati numerici reali, la maggior parte delle informazioni numeriche inizia con la cifra "1" e a seguire le altre cifre. Sembrerebbe un fatto strano, ma è proprio così.
Passando direttamente ai numeri nudi e crudi, la legge afferma che la prima cifra di un numero (in una distribuzione sufficientemente elevata di dati) ha una probabilità di circa il 30% di essere "1", le successive cifre seguono in ordine logaritmico decrescente.
La legge, applicata a distribuzioni di dati empirici, dà quasi sempre la sua validità: essa può essere adottata per verificare, ad esempio, la veridicità di bilanci aziendali, di quantità di popolazione raggruppata per un certo criterio, e così via.
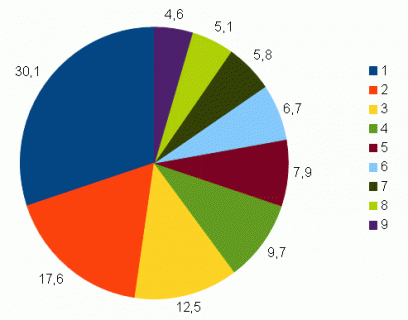
Pertanto, la probabilità che un dato numerico inizi con una certa cifra è la seguente:
Cifra Probabilità
----------------------
1 30.1%
2 17.6%
3 12.5%
4 9,7%
5 7.9%
6 6.7%
7 5.8%
8 5.1%
9 4.6%
Per ottenere la probabilità sopra indicata, oltre che a consultare la tabella, è anche possibile adottare la seguente semplice formula matematica:
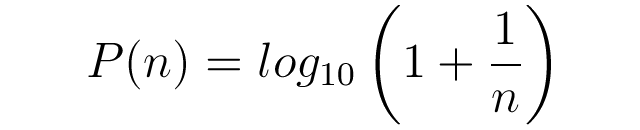
L'andamento della serie può essere anche visualizzata dal seguente pseudo-grafico:
1---------------2---------3-------4-----5----6---7--8--9
Esiste anche una versione più dettagliata della legge, che contempla le coppie di numeri 00..99 anziché le singole cifre unitarie, ma il principio è il medesimo.
Per la corretta applicazione della legge è opportuno che i dati da analizzare sia di numero sufficientemente elevato, onde evitare fenomeni di alterazione dei risultati. Infatti essa va impiegata con la dovuta cautela e se i campioni analizzati fossero in numero ridotto, è molto probabile che la legge di Benford non venga rispettata, anche con dati veritieri.
1° Esempio Pratico
Una azienda riceve il controllo della Finanza, al fine di verificare se le fatture emesse siano veritiere o meno. Il controllo delle 2450 fatture, focalizzato sull'importo dell'imponibile, porta ai seguenti risultati:
Il seguente grafico dimostra che il numero delle fatture, con imponibili che iniziano rispettivamente per "1", "2", "3", ecc (istogramma arancione), rispecchia molto fedelmente l'andamento dettato dalla legge di Benford (istogramma azzurro), pertanto si può ritenere (con ottima probabilità) che l'azienda abbia emesso correttamente i documenti di vendita.
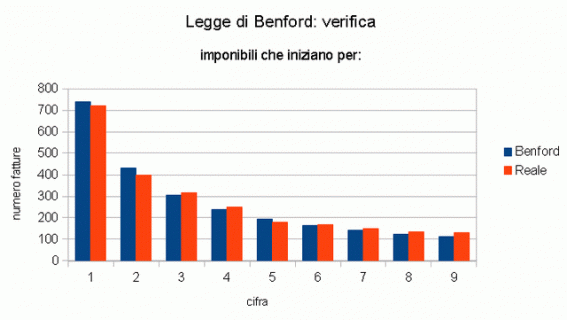
Una fatturazione adulterata avrebbe probabilmente mostrato, al contrario, un andamento alquanto diverso, visualizzando un istogramma irregolare e ben diverso dalla previsione formulata di Benford:
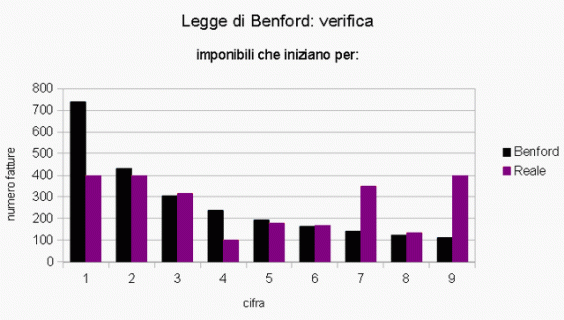
Naturalmente una "non congruenza" con il grafico di Benford non vuol dire che l'azienda abbia commesso per forza un illecito, ma in questi casi è opportuno aumentare l'attenzione poichè potrebbe esserci la probabilità che qualcosa non abbia funzionato a dovere...
2° Esempio Pratico
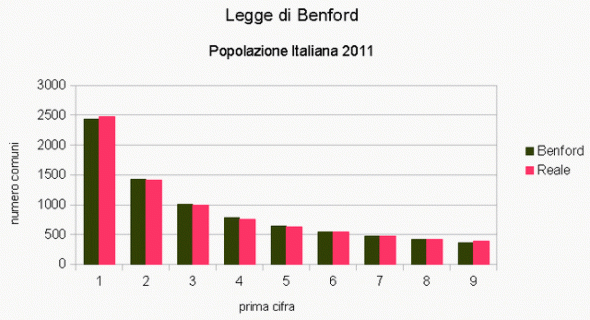
Si è scaricato da Internet il file della popolazione italiana al 2011, suddivisa per comune. Esso contempla ben 8092 comuni. Chi volesse eseguire qualche esperimento può scaricare tale archivio dal link http://lab.comuni-italiani.it/files/listacomuni.zip. Si sono quindi contati i comuni la cui popolazione inizia per "1", poi i comuni la cui popolazione inizia per "2", e così via...
I risultati sono stati impressionanti: il conteggio ha generato i seguenti totali:
Come si nota dalla tabella, Benford ha in pratica "indovinato" quanti comuni hanno una popolazione che inizia per "1", per "2", ecc. Il grafico rinforza ancor di più tale affermazione:
Chi disponesse di tempo e passione può eseguire alcuni interessanti esperimenti di conteggio e verificare dove la legge di Benford funzioni bene o dove essa fallisca e fornisca risultati meno attendibili.
A tale scopo si possono contare le cifre iniziali delle seguenti collezioni:
- Le lunghezze dei fiumi del mondo;
- Il numero dei libri venduti in Italia, negli anni;
- Il numero di cani in ogni nazione del mondo;
- E così via.
Si vedrà che la legge di Benford può ritornare utile in mille occasioni, ricordando però che essa non è una legge assolutamente matematica ma statistica. Occorre pertanto usarla con le "pinze". In ogni caso un elenco "strano" salterebbe subito all'occhio poichè esso, quasi sicuramente, ha violato la regolarità della formula di Benford.
Buona ricerca a tutti.
GDM








Grazie per avermi incuriosito, non ho assolutamente provato a fare dei controlli “carta e penna” autonomamente, ma ho un po’ guardato su google quali altri fit esistessero.
Insomma, se avete tempo da perdere durante queste vacanze pasquali, date un occhio anche voi e magari vi ritroverete come me, a bocca aperta, nel constatare come sia “armonioso” il mondo che ci circonda!
Buona pasqua
Per la serie: “le bugie hanno le gambe corte” 😉
La statistica sa essere uno strumento straordinario, se utilizzato con un minimo di raziocinio.
Ottima lettura!
è proprio vero: le statistiche non sono il verbo!
La gente è così straordinariamente confortata da numeri, percentuali… l’approccio critico ai dati, però, è un’altra cosa…!
Ci sarà qualche collegamento con la sezione aurea e la serie di Fibonacci ?
E chi lo può dire…… la successione di Fibonanacci è stata trovata in molti eventi, anche naturali.
In ogni caso, per ora, la successione di Fibonacci segue la legge di Benford….. in questi giorni sto verificando se anche i numeri PRIMI seguono tale legge………..
In che senso la successione di Fibonacci segue la legge di Benford ? non ho ben capito
Cioè:
prendi la serie di Fibonacci:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, ecc ecc, ecc.
Saranno più numerosi i numeri che iniziano per “1”, poi un po’ meno quelli che iniziano con “2”, e così via.
Ovviamente più è grande il campione preso, più è precisa la stima.
Ho capito.
Insomma, Benford è riuscito nell’impresa che portò, invece, Maximillian Cohen a trapassarsi il cranio con un trapano… come si suol dire, quando la realtà supera la fantasia 😀