In questo articolo ci proponiamo di implementare uno script in ambiente Mathematica per il calcolo del fattoriale inverso (o antifattoriale). Ho letto con estremo interesse l'articolo di Piero Boccadoro sul calcolo del fattoriale inverso tant'è che ho implementato uno script in ambiente Mathematica, il noto sistema di Computer Algebra (C.A.S.).
Prima di addentrarci nella descrizione del programma, vediamo di focalizzare la nostra attenzione sulle difficoltà che si incontrano nel calcolo del fattoriale inverso.
Come descritto nell'articolo citato, il fattoriale è una funzione (o applicazione/operatore) che a ogni numero intero naturale n associa il prodotto n*(n-1)*(n-2)...*2*1 e si indica con il simbolo n!. Ad esempio, il fattoriale di 4 è 4! = 4*3*2*1 =24. Anche 0 ha un fattoriale: si pone per definizione:
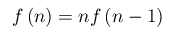 (1)
(1)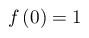 (2)
(2)Ci poniamo, dunque, il problema di "invertire" l'operazione di fattoriale. Dalla formula (1) ricaviamo
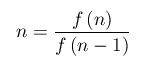 (3)
(3)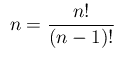 (4)
(4)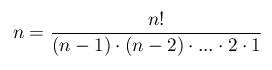 (5)
(5)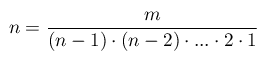 (6)
(6)Un'altra osservazione: non sempre la (6) è compatibile, nel senso che è priva di soluzione. Tale circostanza si verifica, ad esempio, per ogni m dispari. Per m=1 l'equazione è compatibile e indeterminata, poichè ammette due soluzioni: n=0 e n=1. Infatti 0!=1!=1. In tutti gli altri casi, se l'equazione è compatibile, allora è determinata (ammette una ed una soluzione). Questa conclusione ci permette di definire univocamente l'antifattoriale per n>1.
Assegnato m, per risolvere la (5) i.e. trovare l'antifattoriale, dobbiamo "provare" per vari n a partire da n=2, fino a quando risulta soddisfatta la formula (6). Dunque, si tratta di applicare un procedimento iterativo che va ripetuto per un certo numero di passi.
Con Mathematica possiamo utilizzare il ciclo Do, la cui sintassi è Do[<espressione>, {n,n_min,n_max,n_step}], dove n è l'iteratore, n_min e n_max individuano il range del ciclo, mentre n_step ne fissa il passo.
In <espressione> inseriamo un costrutto If la cui sintassi è If[<condizione>,T,F], dove T e F sono gli usuali stati logici True e False, rispettivamente. A questo punto non dobbiamo fare altro che dire a Mathematica di controllare la
n = m/(n-1)!
per un assegnato m e per n variabile in un dato range.
Si noti che l'estremo superiore del range va fissato "ad occhio", nel senso che dipende dall'ordine di grandezza di m. In altre parole, si va per tentativi. E questo può essere fatto con il ciclo Do.
L'equazione rappresenta la condizione e se occupa lo stato logico True, lo script stampa a video il risultato che è appunto il fattoriale inverso di m.

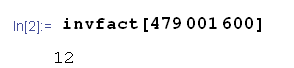







Questo esperimento è diventato un dibattito aperto e io ne sono davvero molto contento 🙂
Chiunque voglia provare e proporre altro, troverà spazio sulle nostre pagine 🙂
Complimenti. L’articolo presenta il problema in modo elegante e rigoroso. Interessante l’utilizzo del calcolo numerico con uno strumento “simbolico” come Mathematica.
Nel merito mi sembra che l’approccio sia lo stesso proposto da Piero, cioè una soluzione iterativa che verifica per ogni naturale se è soluzione. La differenza è soprattutto nel codice (e nell’uso delle strutture di controllo) che consente con poche istruzioni di effettuare lo stesso calcolo. Magari si potrebbe indagare come implementare lo stesso problema in linguaggi/ambienti differenti (e vedere se da qualche parte c’è una funzione predefinita da usare come confronto).
Il punto debole di questo approccio è che deve controllorare tutti i numeri e lo sforzo computazionele è enorme. Stavo pensando ad approcci “alternativi”, ma finora non ho ottenuto risultati e mi sono “rassegnato”alla soluzione iterativa. Se riesco a venirne a capo vi aggiorno.
Concludo con una domanda: sono state fatte delle misure del tempo di calcolo? Magari anche per un confronto con l’algoritmo proposto da Piero.
In effetti al tempo di calcolo non avevo pensato, a me è bastato funzionasse.
Però da un semplice giochino possiamo farlo diventare qualcosa di più.
Che ti aspetti dal tempo di calcolo? Come pensi di ottimizzarlo?
E qui veniamo al metodo. La soluzione iterativa a me è sembrata la più logica perchè i numeri vanno analizzati uno per uno ma in effetti in generale la eviteremmo. Quindi, pensiamoci 😀 Come si può fare a sostituirla?
Si potrebbero generare delle tabelle per delineare dei range di ricerca. Se il valore ricade entro certi range sappiamo che il numero n originante dovrà essere entro un certo range. In questo modo con una semplice ricerca iniziale diminuiamo drasticamente il tempo di calcolo.
Potrei sbagliarmi, ma secondo me è impossibile evitare l’iterazione. Si potrebbe utilizzare l’approssimazione di Stirling: http://it.wikipedia.org/wiki/Approssimazione_di_Stirling. Cioè, invertire la formula di Stirling che, a occhio, sembra possibile solo per via numerica, per cui viene introdotta un’ulteriore approssimazione.
Per ora ho utilizzato interi naturali dello stesso ordine di grandezza di quelli utilizzati nell’esempio riportato nel post. In ogni caso, si potrebbe sfruttare qualche “tecnica di cashing” (che avevo già provato con un altro problema riguardante i numeri primi)
se vogliamo calcolare il fattoriale inverso di:
2283860335914641457397265865115333727042973071546228701773634716126027\
6926030248458777765497919211029457065581960747795750095505232241970499\
5617697230205658766722616606097632340497755473254301355713314682574755\
3799450849523377065894531021055272516334278466875614904921365807833845\
8534285571551800849578848226429898670032945513859929938621783523490272\
6469669185449361408000000000000000000000000000000000000000000000000000\
00
Mathematica impiega 5.42101*10^-19 sec
[Risultato: 220]
Ciao Marcello, mi confermi che leggo bene * 10^-19 !!!!? di che macchina disponi?
Comunque, se provi la variante che ho tentato di abbozzare nella mia risposta a Gianluca, fammi sapere quanto impiega. L’unico criterio semplice per fare confronti sul peso computazionale è fare girare due algoritmi “concorrenti” sulla stessa macchina, così ci si astrae da OS, linguaggio, CPU (numero e velocità) ecc.
Sono curioso.
Non so scrivere in Mathematica ma provo a scrivertela qui. Tu sicuramente saprai metterla in forma corretta.
invfact[m_]:=
A=1;
Do [A = A*n;
If[A == m, Print …..],
{n,1,20},
]
In questo modo, usando la stessa eleganza formale di Mathematica il costo
computazionale è quello di una moltiplicazione (costa meno di una divisione) e
un confronto per ogni ciclo.
È una macchina “vecchiotta”: AMD Athlon 64×2 Dual Core 4600+2.41 GHz, 3.00 GB di RAM
Allego screenshot del Timing dello script di Mathematica a questo link:
http://imagizer.imageshack.us/a/img674/3476/mzE0nQ.gif
ps. appena ho tempo scriverò il tuo script
Sembra che quel valore sia inferiore ad un ciclo di clock, quindi è sicuramente sbagliato. Probabilmente è dovuto alla presenza del dual core, se ho capito bene quel che si dice in questo post:
http://mathematica.stackexchange.com/questions/14152/difference-between-absolutetiming-and-timing
prova AbsoluteTiming
Come suggerito da Gianluca, ho provato con AbsoluteTime. Ecco il risultato: 0.0156250 secondi.
Dalla guida in linea di Mathematica:
Timing just reports CPU time used
Absolute Time get the total time to do a computation
Scusate ma mi sembra un problema molto più semplice di come lo sviluppate.
basta dividere il numero per “n” che va da 2 a …. quando nel risultato compaiono decimali o quando il risultato è 1. Il numero immediatamente prima è l’antifattoriale. Se compaiono decimali l’espressione non ammette soluzione.Primo la fin è sicura senza inventarsi limiti e finisce in un numero di cicli massimo uguale a “n”. Uso il vostro valore di 12! ed esco con 12 come ultimo numero prima dell’ 1
n m
1 479001600
2 239500800
3 79833600
4 19958400
5 3991680
6 665280
7 95040
8 11880
9 1320
10 132
11 12
12 1
qui uso un valore inferiore di 2 ed esco al secondo tentativo
n m
1 479001598
2 239500799
3 79833599,67
Semplice e veloce, no?
Chiedo scusa, ho trovato finalmente l’articolo iniziale e fa esattamente quello che suggerivo io.
Mi sembra così semplice che non capisco la complicazione dello script. Cosa non capisco?
Se poi interpreto correttamente l’espressione, non dovrebbe essere [n, 2,20]? per dire da 2 a 20?
E’ stato scritto che per n=1 si dividerebbe per 0. Devo trovare Mathematica per capire la sintassi.
Ciao, scusate il commento di prima. Sarà ……moderatamente scartato ;-))
Sia l’articolo iniziale di Piero sia questo risolvono il problema. Qual è il valore aggiunto? La dimostrazione che uno stesso problema si può affrontare in modi (e con linguaggi) differenti! L’autore ci ha mostrato una implementazione implicita che usa il calcolo del fattoriale (quell’ (n-1)! a denominatore, per cui anche inziando da 1 non si ha divisione per zero 😉 ) nella ricerca del suo inverso.
Volendo essere pignoli usando un ciclo for si testano tutti i numeri senza una condizione di uscita, mentre nell’algoritmo proposto da Piero è presente la condizione di arresto di cui parli.
Resta la domanda del perché più articoli su uno stesso argomento e perché voler fare diversamente una cosa che già si sa fare: per il gusto di migliorarsi! Le questione che ponevo io era: è possibile trovare un algoritmo che non richieda “n” passaggi, o che limiti le lineee di codice, o che riduca il tempo di calcolo?
Se l’umanità si fosse accontentata della prima soluzione (la più semplice ed immediata) non ci sarebbe stata l’evoluzione! Immaginiamo la scena: perché lavorare del legno per creare ed usare un asse con due ruote quando basta mettere dei tronchi a sezione circolare sotto un oggetto per trasportarlo? 😉 😀
Detto questo l’articolo di Piero presentava un problema abbastanza inusuale tanto da stimolare evidentemente la creatività degli articolisti. Non so se ci sono altri articoli sullo stesso argomento in preparazione ma se ci fosse un articolo che mostri come scrivere un programma in python (ad esempio) per risolvere lo stesso problema, indifferentemente nella versione di Piero o questa o entrambe, sarebbe per me il benvenuto perché mi consentirebbe di concentrarmi solo sul linguaggio e non anche sul problmema che, a questo punto, è ampiamente noto.
Ciao, il mio nome è Gianantonio Moretto ik2ihz (nominantivo redioamatore).
voglio accontentarti con un programma di due istruzioni scritto per Excel.
Non credi che Excel sia capace di gestire numeri così grandi? Da solo magari no ma l’uomo supera sempre i limiti.
Non so come allegare un foglio excel ma ti metto solo due frammenti. Poi mi dite come fare a linkare un foglio Excel alle risposte.
22 8386033591 4641457397 2658651153 3372704297 3071546228 7017736347
2 11 4193016795 7320728698 6329325576 6686352148 6535773114 3508868173
3 3 8064338931 2440242899 5443108525 2228784049 5511924371 1169622724
4 0 9516084732 8110060724 8860777131 3057196012 3877981092 7792405681
5 0 1903216946 5622012144 9772155426 2611439202 4775596218 5558481136
6 0 317202824 4270335357 1628692571 435239867 795932703 926413522
7 0 45314689 2038619336 1661241795 2919319981 8685133243 8703773360
8 0 5664336 1504827417 207655224 4114914997 7335641655 4837971670
9 0 629370 6833869713 3356406136 7123879444 5259515739 537552407
10 0 62937 683386971 3335640613 6712387944 4525951573 9053755240
11 0 5721 5516671542 3030512783 7882944358 8593268324 823068658
12 0 476 7959722628 5252542731 9823578696 9049439027 6735255721
13 0 36 6766132509 404041748 6140275284 7619187617 4364250440
14 0 2 6197580893 2171717267 9010019663 7687084829 9597446460
15 0 0 1746505392 5478114484 1934001310 5845805655 9973163097
16 0 0 109156587 342382155 2620875081 9115362853 4998322693
0 0 17222939 3189537044 7865264423 8929742279
0 0 84014 3381412375 2916415924 5311852401
0 0 407 8365929186 1810273863 8569475011
0 0 1 9702250865 8414542385 3664586835
0 0 0 94722359 8550069915 6988772052
0 0 0 453217 327990765 4339659196
0 0 0 2158 1763466622 7877807900
0 0 0 10 2283239178 7193733686
0 0 0 0 482468109 1260347800
0 0 0 0 2265108 4935494590
0 0 0 0 10584 6191287357
0 0 0 0 49 2307866452
0 0 0 0 0 2279203085
0 0 0 0 0 10503240
0 0 0 0 0 48180
0 0 0 0 0 220
0 0 0 0 0 1
La prima sezione è l’angolo in alto asinistra e potete riconoscere l’inizio del numero di partenza.
La seconda sezione è l’angolo in basso a destra e potete vedere gli ultimi due numeri diversi da 0, Il nostro 220 e poi l’uno.
Piaciuto? Le due equazioni da scrivere sono:
=INT(B11/$A12) nella colonna a destra dei numeri crescenti
=INT((C11+(B11-INT(B11/$A12)*$A12)*10^$A$2)/$A12) in tutte le atre.
…+(B11-INT(B11/$A12)*$A12)*…l’ho scritto per calcolare il resto perchè la funzione RESTO di Excel non mi funziona correttamente.
In pratica ho copiato 10 cifre in ogni casella iniziano da destra e, siccome sono 422 digit ne sono avanzati due da soli.
Poi ho fatto una colonna con tutti i numeri da 2 a ……..quanto vogliamo, tanto si può allungare.
Nella colonna a destra dei numeri in sequenza ho scritto la prima equazione per dividere il numero appena sopra per il numero in prima colonna (notare il $).
nelle colonne successive e fino in fondo alla riga si copia la seconda equazione che calcola il resto della divisione precedente e lo somma moltiplicato per 10^10 al numero sopra esattamente come facciamo noi nelle nostre divisioni ma con gruppi di 10 cifre) e lo dividiamo per il numero in prima colonna.
Facendo così, possiamo fare qualunque divisione con Excel o invertire il tutto e fare moltiplicazioni (ora lo faccio). Mi fermo qui. fatemi sapere se vi è piaciuto.
Gianantonio
Non ho ben capito perché suddividere il numero in gruppi da 10 cifre: c’è una limitazione in excel legata alla precisione o alla possibilità di inserire numeri con un elevato numero di cifre in un cella? Comunque è ingegnosa la soluzione! Così come il calcolo del resto. Quello che mi lascia perplesso, invece, è usare excel per risolvere algoritmi, visto che non è un linguaggio di programmazione vero e proprio.
Se guardiamo all’algoritmo, poi, si “peggiorano” in qualche modo le cose, perché oltre agli “n” confronti, si devono anche scrivere tutti i numeri coinvolti (anche se è semplice farlo con un copia e incolla!) quindi, in astratto, stiamo anche utilizzando male la memoria! 😀
Comunque se ti sei cimentato con una soluzione, vuol dire che l’argomento ti interessa e questo è già una bella cosa. 🙂 Se posso permettermi ti suggerirei di provare a scrivere un post in cui puoi chiarire meglio, anche con l’aggiunta di immagini esplicative, la tua soluzione. In bocca al lupo!
Per n=1 la formula (6) “cade in difetto” perchè implica una divisione per zero. Quindi, tale formula va usata per ogni n>1.
Quando una formula cade in difetto, si utilizza un procedimento differente per risolvere il problema posto. Nel caso in esame, il procedimento “alternativo” è banale, poichè sappiamo che l’antifattoriale di 1 è se stesso, cioè 1.
Scusa se mi permetto ma non concordo.
1 è un valore che ha 2 antifattoriali 1 e 0 per definizione.
Lo so (mi era sfuggito). Infatti, è scritto all’inizio dell’articolo che, per definizione, si pone 0!=1. Quindi, a rigore l’applicazione che definisce il fattoriale è iniettiva in N\{0,1}.
L’iniettività è vitale perchè ci garantisce l’invertibilità dell’applicazione.
ps. Per “applicazione” intendo una legge del tipo f: A->B, dove A e B sono insiemi assegnati; f è una legge che associa a ogni elemento di A uno ed un solo elemento di B. Nel caso del fattoriale, A e B coincidono con N, l’insieme degli interi naturali. In realtà, stiamo parlando di una “successione” che è un caso speciale di applicazione. Più precisamente, di successione di elementi di N. Il problema è che si tratta di una successione “ricorsivamente” definita. Ad esempio, se ho una legge del tipo f(n)=(-1)^n, questa mi definisce una successione di elementi di n e posso calcolare l’elemento n-esimo per ogni n da quella formuletta. Con il fattoriale invece si ha f(n)=n*f(n-1). In parole povere, i valori assunti per un dato n, dipendono da quelli precedenti (ricorrenza). Ed è proprio la ricorrenza che impedisce di invertire il fattoriale in forma chiusa. Come dicevo nell’altro commento, si potrebbe provare ad invertire la formula di Stirling dopo avere esteso il fattoriale ai numeri reali. Cosa strana, ma è possibile definire il fattoriale anche per i reali. Ciò è una conseguenza di una proprietà di una fuzione speciale della fisica matematica nota come “funzione euleriana gamma”. Ma la funzione (o formula) di Stirling è si invertibile, ma non l’inversa non è dotata di espressione elementare. La funzione di Stirling è: f(x)=x^x * e^(-x) * sqrt(2*pi*x). L’unico modo è ricorrere a qualche sviluppo in serie, dopodichè prendere la parte intera del risultato. Ma in questo modo aumenta il tempo di computazione e per grandi valori della variabile indipendente sembrerebbe addirittura impossibile. In merito a questo: anzichè utilizzare i numeri primi, non si potrebbe inventare un qualche metodo crittografico che utilizza il fattoriale inverso per grandi valori di x??
Errata corrige: “per ogni m dispari. Per m=1…”
sostituire con: “per ogni m dispari eccetto m=1. Per m=1…”
Se guardiamo alla storia della matematica (anche quella recentissima) vediamo che esiste una relazione profonda tra la teoria dei numeri e altri rami della matematica. Un esempio è dato dalla famigerata ipotesi di Riemann in cui la distribuzione dei numeri primi è collegata alla teoria delle funzioni di variabili complesse. Un altro esempio, ancora, è dato dalla dimostrazione dell’ultimo teorema di Fermat.
Anche il “fattoriale di n”, argomento che riguarda il calcolo combinatorio, sembra non fare eccezione. Come dicevo nell’altro commento, è collegato alla funzione gamma che non ha nulla a che vedere con il calcolo combinatorio e che permette di estendere la nozione di fattoriale anche ai numeri non interi. Sto cercando di ricavare una qualche formula approssimata in modo da poter calcolare l’inverso del fattoriale anche per valori molto elevati della variabile. Fino ad ora ho scritto questo:
http://hypercyber.it/formula_stirling.pdf
Complimenti. Effettivamente è un problema complesso (anche nel senso dell’analisi complessa 😀 ). Non sono fiducioso che si possa trovare un metodo approssimato perché all’aumentare del numero l’errore sembra non più recuperabile. Per questo sto pensando ad un modo per migliorare l’algoritmo di ricerca che non sia basato su formule di inversione tipo quelle che citi. Spero di riuscire a scrivere un post quanto prima. 🙂
Provo a mostrare una applicazione pratica del mio metodo semplificativo.
Sia dato il numero:
8683317618811886495518194401280000000
col metodo degli Zeri calcolo il suo ipotetico antifattoriale:
=N = (Z – int (Z/6))*5 = (7-int(7/6))*5 = (7 – 1) * 5 = 6 * 5 = 30
Quindi una buona stima è che il nostro numero sia >= 30!
Calcoliamo la fattorizzazione di 30!
I primi minori di 30 sono : 2,3,5,7,11,13,17,19,23,29
con int(30/2)= 15; int(15/2)=7;int(7/2)=3;int(3/2)=1 da cui 2^26
int(30/3)= 10; int(10/3)=3;int(3/3)=1 da cui 3^14
int(30/5)=6;int(6/5)=1 da cui 5^7
int(30/7)=4 da cui 7^4
int(30/11)=2 da cui 11^2
int(30/13)=2 da cui 13^2
int(30/ ogni cosa > 30/2) = 1 da cui 17^1,19^1,23^1;29^1
Abbassiamo gli esponenti di 2 e 5 di 7 e abbiamo 2^19 e 5^0
Togliamo gli zeri e resta 868331761881188649551819440128
dividiamo per
2^19 = 2^9*2^9*2 = 512 * 512 * 2 = 524288
e abbiamo 1656211398851754473785056 intero
dividiamo per 3^14 = 4782969
e abbiamo 346272660109600224 intero
non dividiamo per 5 perchè (5^0) = 1
dividiamo per 7^4 = 2401
e abbiamo 144220183302624 intero
dividiamo per 11^2 = 121
e abbiamo 1191902341344 intero
dividiamo per 13^2 = 169
e abbiamo 7052676576 intero
dividiamo per 17
e abbiamo 414863328 intero
dividiamo per 19
e abbiamo 21834912 intero
dividiamo per 23
e abbiamo 949344 intero
dividiamo per 29
e abbiamo 32736 intero
dividiamo adesso per 31, poi 32 ecc, fino a 34 cercando il primo decimale
diviso 31 otteniamo 1056
diviso 32 otteniamo 33 FINE
quindi il nostro numero è un fattoriale puro e vale 33!
Proviamo adesso a cambiare una qualunque cifra, ad esempio invece di 86….. scriviamo 76…. che non può essere un fattoriale puro (già fallirebbe il criterio di divisibilità per tre a priori)
Ovviamente il criterio degli zeri porterà alla stessa situazione di prima e adesso passiamo alla
fase di verifica.
Togliamo gli zeri e resta 768331761881188649551819440128
dividiamo per
2^19 = 524288
e abbiamo 1465476535570504473785056 intero
dividiamo per 3^14 = 4782969
e abbiamo 306394738408403745,9257 decimale
Quindi abbiamo verificato che il numero 768331…..
non è un numero fattoriale puro.
Secondo me non è male ;-)) Ciao.
Metto due post insieme: un’idea per il calcolo rapido del fattoriale euno per l’approssimazione del calcolo dell’antifattoriale.
Una maniera semplificata per il calcolo del fattoriale l’ho trovata in questo
modo:
17! = 2^15 x 3^6 x 5^3 x 7^2 x 11 x 13 x 17 dove 2^15 si ottiene in questo
modo:
int(17/2) = 8, 8 è >2 quindi aggiungo 8/2 = 4 che è >2 quindi aggiungo 4/2 = 2 che è
> =2 quindi aggiungo 2/2 = 1 ottenendo
2^(8+4+2+1) = 2^15
int(17/3)= 5 ma 5>=3 quindi int(5/3) = 1 ottenendo 5^(5 + 1) = 3^6
int(17/5) = 3 e 3<5 quindi 5^3
int(17/7) = 2 e 23 –> int (10/2) = 5; 5>=2 –> int(5/2) = 2;
2>=2 –> int (2/2) = 1 2^(10 + 5 + 2 + 1) –> 2^18
int(20/3) = 6; 6>3 –> int (6/3) = 2; 2<3 stop 3^(6 +2)
int(20/5) = 4; 4<5 stop 5^4
int(20/7) = 2; 2=25 Z=int( N / 5 + N/25) = int ((5N + N)/25) circa= (6N/25)
Per N >=125 avremo un ulteriore zero in più e quindi Z = int(N/5) + int(N/25)
+ int (N/125) = (25N + 5N + N)/125
Invertendo il calcolo abbiamo N = Z x 5 tra 0 e 24, N = Z x 25 / 6, N = Z x
125 / 31 dove N è il massimo antifattoriale multiplo di 5.
Partendo da questo concetto, ho sviluppato questa regola:
Dato il numero degli zeri, si moltiplica questo numero per 5; se il risultato
è > 24 si applica la formula successiva N = (Z-int(Z/6)*5 ; (Z – int(Z/6)-int
(Z/31))*5) questo è il fattoriale inferiore multiplo di cinque. Il nostro
antifattoriale (se esiste) è compreso fra il numero ottenuto e quello più
grande di 5.
Faccio qualche esempio: 355 687 428 096 000 è il fattoriale di 17.
Gli zeri sono 3 quindi N = 3 x 5 = 15 > di 125 per cui salto alla terza formula N = (53 –
int (Z/6) – int (Z/31)) x 5
N = (53 – 8 – 1) x 5 = 44 x 5 = 220
ESATTAMENTE COME DETTO (e verificato) NEL PRECEDENTE POST.
Si procede con le formule successive che vi risparmio.
Si può adesso cercare l’antifattoriale sapendo che si trova tra 220 e 224.
TUTTO RAGIONANDO SOLO SUL NUMERO DEGLI ZERI.
Adesso sto cercando di trovare qualche metodo che permetta di approssimare
meglio l’antifattoriale ma non sono un matematico e ormai sono lontano 40 anni
dai ricordi universitari. Mi sembra comunque un risultato interessante (anche
se non degno dell’accademia di matematica a me è piaciuto).
Spero di essere stato sufficientemente chiaro per farmi capire.
Ciao ;-))
PS a proposito, la formula successiva è N = (Z -int(Z/6) – int(Z/31) – int
(Z/156)) x 5. Verificate però.
Nel post precedente dove avevo usato Excel per fare i conti, ho solo cercato di dimostrare che si possono superare i limiti di un programma di calcolo ricorrendo a una riutilizzazione di quanto imparato alle …elementari. Ovvero come si fa una divisione.
Mathematica probabilmente è scritto per fare calcoli in modo più flessibile di Excel ma anche C, Phyton, Fortran e tutti gli altri sw non specialistici hanno un max numero di cifre significative.
Per superare questo limite basta usare un array e applicare agli elementi dell’array i concetti espressi per Excel. Attenzione ai limiti di precisione, comunque. Occorre spezzare il numero in gruppi di cifre tali per cui il prodotto non esca dal numero di cifre significative.
Un esempio: 8 cifre significative vuol dire che non posso fare moltiplicazioni tra numeri che abbiano più di 7 cifre significative in totale 123 x 4567va bene, 1 x 234567 anche ma anche 123456 x 7. Quindi valutate bene il massimo numero di cui volete calcolare il fattoriale.
Se volete arrivare a 8765, avete già consumato 4 cifre significative. Excel ne usa 15 max, ergo i gruppi di cifre dell’array non potranno essere più di 10.
La dimensione dell’array dovrà essere quindi pari all’ordine di grandezza del risultato atteso / 10.
Se pensiamo che il risultato sarà di 250 cifre, avremo un array di almeno 25 celle.
L’utilizzo della memoria è quindi ottimizzato perchè possiamo calcolare resto e quoziente in una singola cella e fare le operazioni (sia fattoriale che antifattoriale) sul posto, come si dice in gergo.
Mi sto facendo prendere dalla voglia di continuare. Qualcuno più bravo di me mi dia un’idea se sono sulla strada giusta o meno.
Ciao a tutti
Ho provato a realizzare in Simulik uno schema per l’inversione del fattoriale sfruttando la proprietà della retroazione di invertire le funzioni. Sono riuscito nello scopo, ma alla fine il numero di passi richiesti è sempre dell’ordine del numero da indentificare. Non riuscendo a migliorare l’algoritmo e non sapendo come allegare figure al commento non mi dilungo nella descrizione. Ritengo comunque interessante la possibilità di “costruire” un sottosistema riutilizzabile in uno schema Simulink.