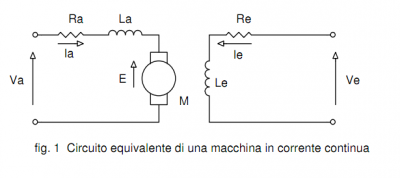
Come vedremo l'implementazione del modello matematico è stata realizzata partendo dalle equazioni che modellano il corretto funzionamento del motore DC, realizzando sucessivamente un modello in ambiente Simulink di Matlab.
Dal punto di vista matematico il motore DC può essere modellato con un sistema di sei equazioni
differenziali lineari:
Va = La*dia/dt + Ra*ia + eg
eg = Kφω
Cm = Kφia
Cm = Bω + Jdω/dt + Cext
Vf = Rfif + Lfdif/dt
φ = Nif/R
Il controllo del motore può essere effettuato sia agendo sul circuito di armatura, sia su quello di
eccitazione. Supponendo che il flusso φ sia costante è possibile semplificare il modello, andando a
considerare il solo controllo sul circuito di armatura, e giungendo ad un modello costituito da sole
quattro equazioni differenziali:
Va = Ladia/dt + Raia + eg
eg = Kφω
Cm = Kφia (Cm è la coppia meccanica)
Cm = Bω + Jdω/dt + Cext
Passando al dominio di Laplace, è possibile giungere alle seguenti quattro equazioni algebriche:
Va – Eg = Ia (sLa + Ra)
Eg = Kv*Omega
Cm = KtIa
Cm – Cext = (sJ + B)
Da queste equazioni è possibile ricavare il seguente schema a blocchi:
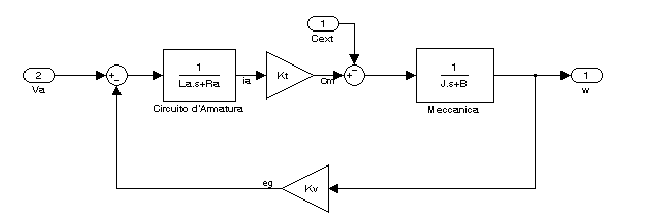
Da tale schema è possibile ricavare la funzione di trasferimento generica del motore riportata di seguito:
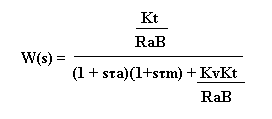
Come si può vedere il motore è già dotato di una retroazione negativa, quindi i poli che il sistema mostrerà all’esterno saranno diversi dai poli meccanico ed elettrico posti sulla catena diretta dello schema a blocchi.
Sostituendo i valori calcolati dai dati di targa del motore lo schema del motore
si particolarizza nel seguente modo:
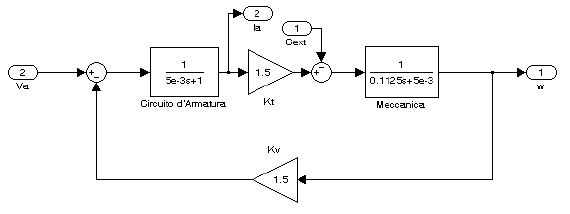
Dove le funzioni di trasferimento sono rappresentate nella figura successiva:

Di seguito invece riportiamo gli andamenti della velocità angolare e della corrente, ottenuti mediante l’applicazione della tensione nominale di 250 V per un tempo pari a 3 secondi :
.png)
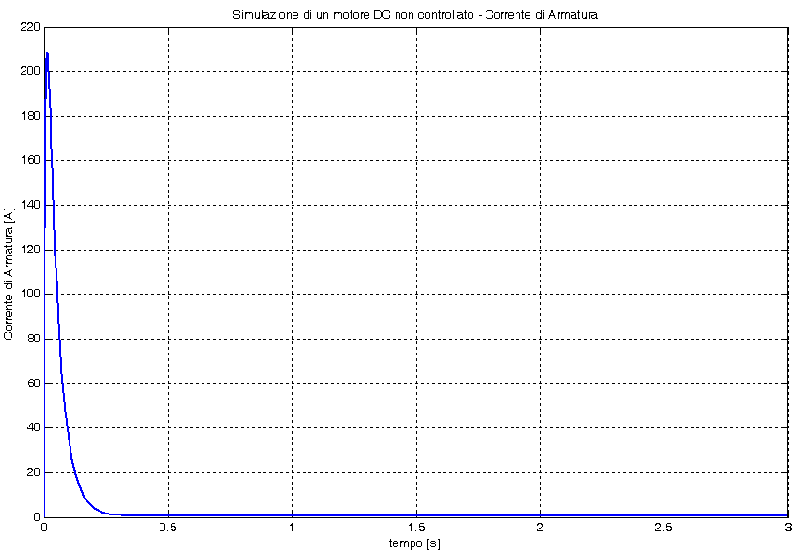
Come si può vedere dal grafico della corrente di armatura, il motore presenta un problema nella fase di avviamento. In questa fase la velocità angolare, che cresce con una dinamica molto lenta rispetto alla corrente di armatura, è molto piccola; di conseguenza la forza controelettromotrice indotta sarà anch’essa piccola rispetto alla tensione di armatura applicata.
Essendo la tensione applicata al circuito di armatura pari alla differenza fra la Va e la Eg, ne consegue che in questa fase la corrente raggiunge un picco che può danneggiare il motore. Si rende quindi necessario effettuare un controllo della corrente di armatura che limiti il valore del picco.
CONTROLLO DELLA CORRENTE DI ARMATURA:
Prima di procedere all’inserimento del circuito usato per la limitazione della corrente di armatura, è bene soffermarsi sull’introduzione dell’amplificatore di potenza. Tale amplificatore è necessario poiché i segnali normalmente prodotti dai regolatori per l’attuazione, sono di poche unità di volt. Esso è stato simulato con il seguente schema a blocchi:

L’amplificatore è realizzato mediante un semplice guadagno posto in serie ad un blocco di saturazione; quest’ultimo blocco modella il fatto che ogni amplificatore reale presenta una inevitabile saturazione. Nel nostro modello si è scelto di utilizzare come estremi di funzionamento in regione lineare dei valori di poco superiori alla tensione nominale di 250 V.
Per raggiungere la tensione nominale sarà necessario un segnale di attuazione di 10 V, mentre per ottenere la tensione
di saturazione (300 V) bisognerà applicare un segnale di 12 V.
Lo schema generale viene modificato come segue:
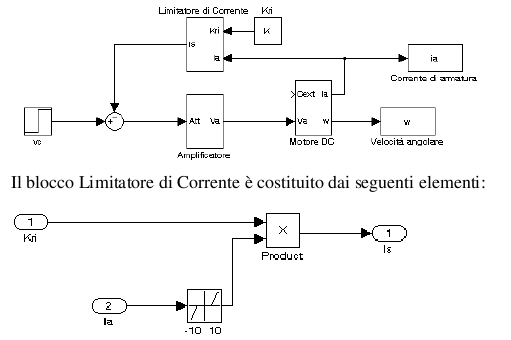
Fintanto che la corrente di armatura si mantiene al di sotto del valore nominale, il limitatore di corrente non interviene, ed in ingresso all’amplificatore si presenta il semplice segnale vc di attuazione.
Quando Ia supera il valore nominale, allora il valore di eccesso di corrente viene moltiplicato per un’opportuna costante Kri. Il segnale in ingresso all’amplificatore è la differenza tra il segnale vc e la tensione uscente dal limitatore. Dunque nel momento in cui interviene il limitatore di corrente, si ha una riduzione della tensione di armatura applicata al motore, con una conseguente diminuzione della corrente.
Solitamente il motore funziona con una corrente di armatura non maggiore di quella nominale; in alcune occasioni può essere conveniente avere una corrente di lavoro superiore a quella nominale al fine di ottenere migliori prestazioni dinamiche del motore. Per ottenere ciò è necessario dimensionare in maniera opportuna la costante Kri.
Per definire Kri sarà necessario fissare un valore massimo di corrente di armatura consentito; in corrispondenza di questo valore il segnale in ingresso all’amplificatore dovrà essere nullo.
In base alle prove effettuate si è constatato che all’aumentare del Kri la dinamica del motore diventa meno spinta e quindi è necessario trovare un compromesso tra la dinamica del motore e la massima corrente consentita. Di seguito sono riportati i grafici relativi a tali prove.
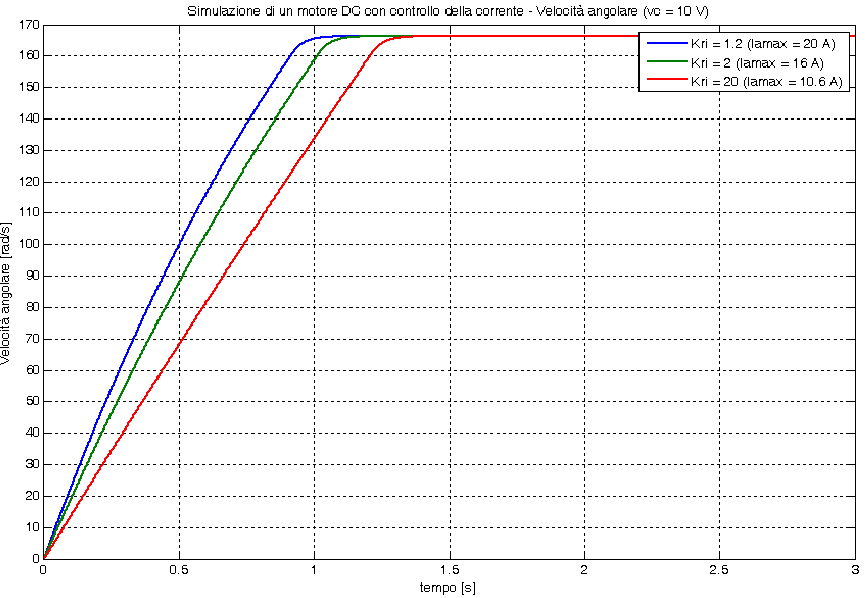
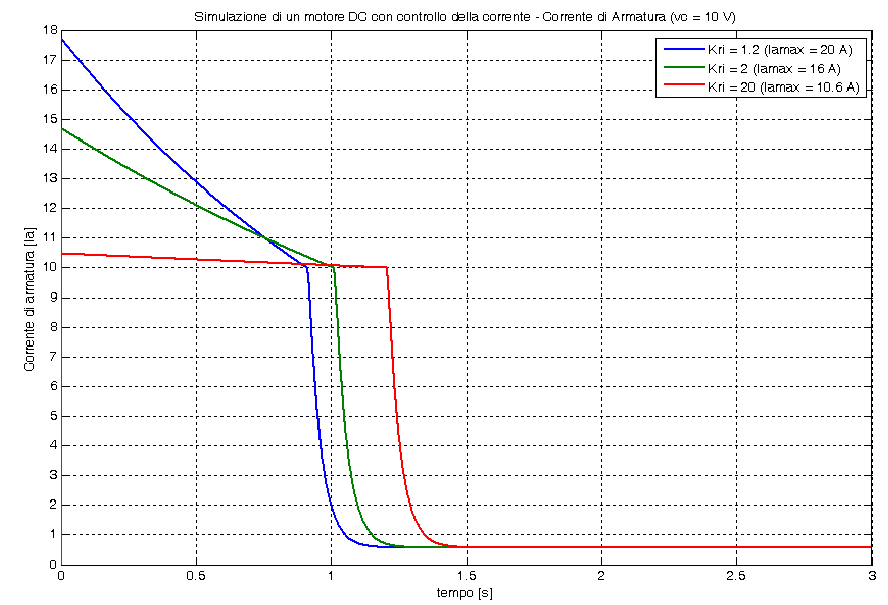
Per le successive simulazioni abbiamo deciso di adottare un valore di Kri tale da consentire una massima corrente di armatura pari a 16 A (1.6 Ian). Il valore di Kri sarà quindi pari a 2 (andamenti in curva verde dei grafici precedenti).
Questo articolo è parte di una tesina sul controllo di un motore in corrente continua. Analisi e progetto con Matlab/Simulink