Ora che siamo a conoscenza dei passaggi da eseguire per realizzare la crittografia (articolo "Algoritmo di crittografia RollingCode"), non ci rimane che approfondire il funzionamento della Encryption Routine che è il cuore di tutta la procedura di crittografia. Grazie a questa routine infatti vengono generati i codici che corrispondono alle informazioni crittografate.

Come per gli articoli precedenti, anche in questo caso la routine di crittografia può essere spiegata attraverso uno schema che racchiude e rappresenta gli step che l’algoritmo deve eseguire:

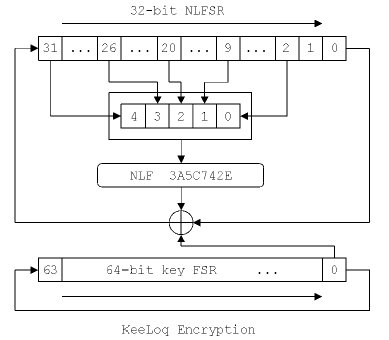
Prima di passare alla spiegazione nel dettaglio dell’algoritmo, vediamo quali sono gli “attori” che entrano in gioco: partendo dall’alto in basso delle figura incontriamo una word a 32 bit che corrisponde al valore che dovrà essere criptato; più in basso abbiamo la NLF, ossia la “Non Linear Function”, la quale esegue la crittografia vera e propria generando ad ogni ciclo un bit il cui valore dipende da cinque bit di ingresso opportunamente selezionati; sotto la NLF troviamo un’operazione di OR eseguita tra una serie di bit (tra cui anche quello generato dalla NLF) e ancora più sotto il registro a 64 bit che contiene la chiave per la crittografia, la quale è stata ricavata attraverso i passaggi visti e descritti nell’articolo “Algoritmo di crittografia RollingCode”.

Ora che abbiamo chiaro quali sono i dati che sono necessari per eseguire la crittografia, possiamo procedere con la spiegazione per punti dell’algoritmo:

1. Come prima cosa devono essere prelevati i bit 2, 9, 20, 26 e 31 dal codice a 32 bit da criptare, per andare a costruire una word formata da 5 bit.

Considerando ad esempio “FDB97531” (è stata adottata la notazione esadecimale per comodità e visibilità nella stesura dell’articolo e considerata una rappresentazione dei bit di tipo big-endian) come word a 32 bit da dover criptare e prelevando i bit 2, 9, 20, 26 e 31, ottengo una la seguente word a 5 bit: “11100”.

2. La word a 5 bit precedentemente ricavata, deve essere sottoposta in ingresso alla NLF la quale fornirà in uscita un solo bit che sarà funzione dei valori dati in ingresso.

Per ottenere il bit di uscita dalla NLF non vengono richieste particolari operazioni in quanto, questa funzione può essere rappresentata attraverso una tabella mostrata nella figura seguente:

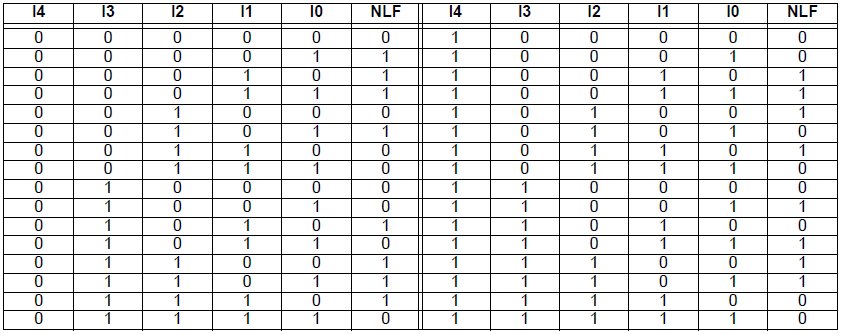
le colonne “I4”, “I3”, “I2”, “I1” e “I0” corrispondono rispettivamente ai bit 31, 26, 20, 9 e 2 del codice da criptare, mentre “NLF” rappresenta il bit di uscita della funzione.

Riprendendo l’esempio precedente avremo che dalla word “11100” a 5 bit otteniamo come risultato il bit “0”.

3. Ora che si ha a disposizione il bit dalla “NLF” occorre sottoporlo ad una operazione di OR con il bit 0 della parola da criptare e con il bit 0 della chiave di crittografia, in modo da ottenere un ulteriore bit risultato dell’operazione.

Supponiamo di avere come chiave “0011223344556677” (anche in questo caso è stata considerata una rappresentazione dei bit di tipo big-endian) e di considerare sempre come parola da criptare il valore “FDB97531”; a questo punto, facendo l’operazione di OR con i bit indicati precedentemente si ottiene: 0 OR 1 OR 1 = 1.

4. Dopo aver ricavato il bit di uscita dall’operazione di OR, deve essere eseguito uno shift di un bit verso destra (verso il bit meno significativo) della parola da criptare.

Considerando l’esempio precedente, la parola “FDB97531” diventerà “7EDCBA98”.

5. Una volta eseguito lo shift, deve essere eseguita un’operazione di sostituzione del bit 31 della parola appena shiftata, con il bit risultato dell’operazione di OR ricavato nel passo “4”.

Rifacendoci sempre all’esempio precedente la word a 32 bit, che dopo la rotazione aveva il valore “7EDCBA98”, ora assumerà il valore “FEDCBA98”.

6. Un’ultima operazione da eseguire è quella di eseguire una rotazione verso destra (verso il bit meno significativo) della chiave usata per la crittografia.

Il valore della chiave che prima era pari a “0011223344556677”, ora assume il valore “80089119A22AB33B”.

7. I punti dall’ “1” al “6” devono essere ripetuti per un numero di volte pari a 66.

Alla fine dei 66 cicli sulla parola a 32 bit che doveva essere criptata è presente il valore criptato e pronto ad essere utilizzato.

Lettura consigliata: Introduzione alla codifica RollingCode

Ti potrebbe interessare anche:

Corso sugli Aeromobili a Pilotaggio Remoto partendo da zero: simulatore di scenari e sistemi di riconoscimento

Protezione del codice su LPC1700

Aritmetica BCD per AVR

Articoli Correlati

Algoritmo di crittografia RollingCode

Algoritmo di decrittografia RollingCode

Introduzione alla codifica RollingCode