
In questo secondo studio (al seguente link lo studio precedente) si è proceduto alla ricerca di una possibile origine degli elementi appartenenti a P* considerando l’equazione y = mx + a e facendo assumere ad a, x ed m solo valori relativi a numeri primi. In seguito è stato definito il concetto di cardinalità polinomiale utile per una caratterizzazione dell’insieme dei numeri primi stesso.
INTRODUZIONE
Il Teorema fondamentale dell’aritmetica spiega l’origine dei numeri non primi appartenenti a W in quanto considera un insieme già dato: P*.
Il teorema di Dirichlet afferma che in ogni progressione aritmetica y = mx + a con (a, m) = 1 si trovano infiniti primi. In altri termini dati due numeri interi coprimi a e m, esistono infiniti primi della forma mx + a, dove m > 0 (x ∈ N).
Procedendo nella ricerca di un’origine ricorsiva dell’insieme P* ho avuto modo di realizzare un inquadramento sistematico dei numeri primi operato sulla base di una restrizione del dominio del polinomio di primo grado y = mx + a in quanto ho limitato i valori assumibili da m, x ed a al solo insieme dei numeri primi P*.
Il teorema di Dirichlet non dice che esistono infiniti numeri primi consecutivi in progressione aritmetica, quindi il medesimo non garantisce che tutti i numeri primi possano essere scritti secondo il polinomio di primo grado y = mx + a eppure ho avuto modo di evidenziare che, una restrizione dei termini x e a del polinomio P (x, a) = 2x + a (con P (x, a) > 5) al solo campo P*, è in grado di generare numeri primi in successione. Non solo. Per numeri primi maggiori di 7 il numero di coppie x, a risulta maggiore di 2. Il numero dei polinomi relativi a tali coppie definisce quella che ho chiamato cardinalità polinomiale cp.
Al momento possiamo affermare quanto segue.
ENUNCIATI
Siano dati l’insieme singolare Σ = {1,2} e la formula P (x, a) = 2x + a dove P (x, a) ∈ P*e x, a ∈ Σ.
- Risulta possibile generare l’ insieme di prima specie Π = {3,5} dove Π ⊂ P* e x, a ∈ Σ
- 2 è l’unico elemento appartenente all’insieme P* ∩ Σ;
- CONGETTURA: Dato l’insieme {2} ∪ Π risulta possibile generare ricorsivamente l’insieme di seconda specie S = P*\ {2} ∪ Π in cui ogni elemento risulta caratterizzato da una cardinalità polinomiale cp ≥ 1 e dove x, a ∈ P*. Quindi si ha P (x,a) = P (px, pa) = 2px + pa.
Esempi:
- P* = {2} ∪ Π ∪ S e Π ∩ S = ∅
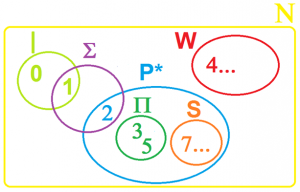
- L’insieme N risulta caratterizzato in accordo alla figura 1.
- Riguardo alla funzione successore S: N → N di Peano possiamo affermare:
- applicata all’elemento minore im ∈ I risulta così definita:
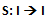
- applicata all’elemento maggiore iM∈ I risulta così definita:

- applicata all’elemento minore pm ∈ P* risulta così definita:
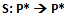 (unico caso in cui S risulta definita in P* ed a valori in P*);
(unico caso in cui S risulta definita in P* ed a valori in P*); - applicata ad un elemento p ∈ P*\{pm} risulta così definita:
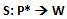
- applicata ad un elemento w ∈ W la funzione S risulta così definita:
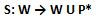
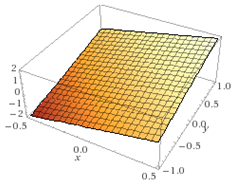
- Da un punto di vista geometrico P (x, a) = 2x + a corrisponde (figura 2) al piano generatore πγ.
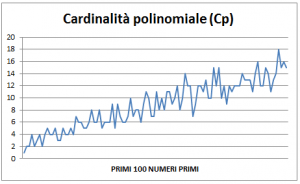
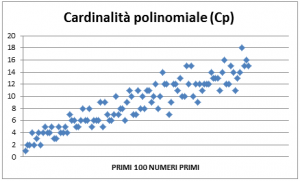
Riportiamo in figura 3 l’andamento della cardinalità polinomiale cp dei primi cento numeri primi.
TEOREMA
Teorema 1. (Teorema sui sottoinsiemi cardinali polinomiali di S). In base alla cardinalità polinomiale cp l’insieme di seconda specie S ⊂ P* risulta composto dall’unione di sottoinsiemi cardinali polinomiali Cn costituiti da elementi aventi tutti lo stesso valore di cp.
Dimostrazione.
1) il sottoinsieme cardinale polinomiale unario C1 risulta formato dagli elementi aventi cp = 1, (C1 = {7}, #(C1) = 1);
2) il sottoinsieme cardinale polinomiale binario C2 risulta formato dagli elementi aventi cp = 2, (C2 = {11, 13, 19, 31}, #(C2) = 4);
3) il sottoinsieme cardinale polinomiale ternario C3 risulta formato dagli elementi aventi cp = 3, (C3 = {23, 59, 61}, #(C3) = 3);
4) il sottoinsieme cardinale polinomiale quaternario C4 risulta formato dagli elementi aventi cp = 4, (C4 = {17, 29, 37, 43, 47, 71, 73, 83}, #(C4) = 8).
...
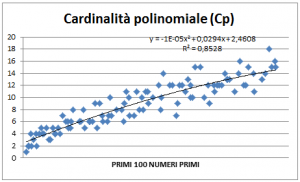
In figura 4 è riportato il grafico a dispersione relativo alla cp dei primi cento numeri primi.
Attraverso il metodo dei minimi quadrati si è cercata la funzione che meglio approssimasse i dati.
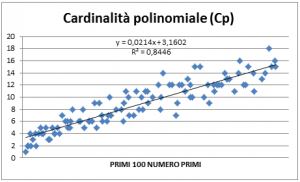
Per quanto riguarda la retta y = bx + a sono stati trovati i seguenti coefficienti (figura 5):
Nel caso della parabola y = ax2 + bx + c risolvendo il seguente sistema:
sono stati trovati i seguenti coefficienti: a = -1 * 10-5, b = 0,0294, c = 2,4608, r = 0,9235
Come si può notare dal quadrato del coefficiente di correlazione di Pearson R (R2 = 0,8528) la parabola y = -1*10-5x + 0,0294x + 2,4608 approssima (figura 6) meglio i dati relativi alla cp.
Un ulteriore studio potrebbe consistere nell’individuare altri polinomi in cui la restrizione delle variabili al solo insieme P* genera numeri primi ed individuare tutte le relative cardinalità polinomiali.


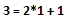
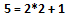
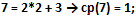

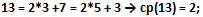
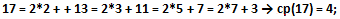
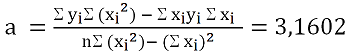

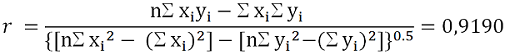
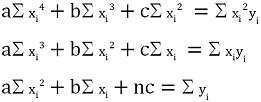






La matematica applicata in questo articolo e’ di notevole rilevanza, complimenti all’autore; attendiamo l’ultima puntata per la prossima settimana.
Ciao Maurizio,
ti ringrazio molto per il complimento.
Articolo originale, complimenti.
Gent.mo Marcello,
sei stato molto gentile nel leggere l’articolo e nell’ esporre il tuo commento positivo.