
In questo studio si è proceduto alla ricerca di una possibile origine degli elementi appartenenti a P* secondo l’approccio generazionista (già presente nella teoria degli insiemi) in cui è possibile, grazie all’introduzione dei numeri ordinali da parte di Georg Cantor (San Pietroburgo 1845 – Halle 1918), costruire tutti i numeri naturali partendo dall'insieme vuoto e considerando di volta in volta l'insieme che ha come suoi elementi tutti gli insiemi precedentemente costruiti. Anche in questo studio si procederà a individuare tutti i numeri primi partendo da due matrici fondamentali e considerando, di volta in volta, l'insieme contenente tutti i numeri primi generati precedentemente.
INTRODUZIONE
La mia indagine è proseguita alla ricerca della possibile origine del sottoinsieme P* ⊂ N. Per far questo si è resa necessaria l'introduzione delle matrici primali.
Una matrice primale Q è una matrice i cui elementi sono costituiti esclusivamente da elementi primi positivi (Q ∈ P*m,n).
Possiamo formulare i seguenti 5 assiomi:
1) Q ∈ P*2,2 è generatrice ⇔ det(Q) ∈ P*∧ det(Q) ≠ qij, ∀ qij ∈ Q;
2) Q ∈ P*2,2 è generatrice assoluta ⇔ det(Q) ∈ P*∧ det(Q) > qij, ∀ qij ∈ Q;
3) Esiste un tipo di matrice generatrice assoluta chiamata matrice generatrice perfetta i cui elementi sono numeri primi consecutivi ed il cui determinante è il numero primo successivo dell’elemento maggiore della matrice:
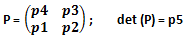
4) Nei casi in cui vale il punto 1) ma non il punto 2), Q è una matrice generatrice semplice;
5) Nel caso di una matrice generatrice Q ∈ P*2,2, essendo una matrice quadrata, risulta generatrice anche la matrice trasposta QT in quanto det(Q) = det(QT).
ESEMPI:
a) matrice A non generatrice:
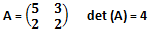
b) matrice B non generatrice:
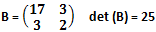
c) matrice C generatrice semplice:
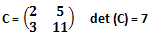
d) matrice D generatrice assoluta:
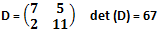
e) matrice E generatrice perfetta:
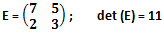
TEOREMI
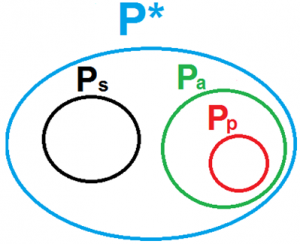
Teorema 1. (Teorema sulla generazione matriciale di P*) Partendo dalla matrice primale 2 ∈ P*1,1 e dalla matrice primale 3 ∈ P*1,1 (matrici primali fondamentali) è possibile ricavare tutti gli altri elementi appartenenti a P* attraverso un processo ricorsivo, mediante il calcolo del determinante di matrici generatrici Q ∈ P*2,2 i cui elementi qi,j appartengono all’insieme Γ ⊂ P* formato dall'unione dell'insieme delle matrici primali fondamentali e dell'insieme dei determinanti delle matrici generatrici calcolati precedentemente (figura 1).
In base alla generazione matriciale, i numeri primi si distinguono in numeri primi assoluti perfetti (cioè ricavabili come determinati di matrici generatrici assolute perfette e formanti il sottoinsieme PP), numeri primi assoluti (cioè ricavabili come determinati di matrici generatrici assolute e formanti il sottoinsieme PA) e numeri primi semplici (ovvero ricavabili come determinati di matrici generatrici semplici e formanti il sottoinsieme PS).
Dimostrazione. Sappiamo che un numero dispari D’ può essere scritto come la differenza tra un numero pari Pa e un numero dispari D’’:
Dal lemma di Chen sappiamo che ogni numero pari Pa è la somma di due numeri naturali P + a con P primo e dove a o è primo o è un prodotto di due primi Px e Py (entrambi diversi da 2). Quindi possiamo scrivere:
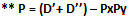
Ma (D’ + D’’) è pari quindi (D’ + D’’) = 2K con K ∈ N* da cui:
Dato che P* ⊂ N allora possiamo anche scrivere:

con P, Pz, Px, Py ∈ P*, PxPy ∈ 2N* + 1 e |2Pz| > |PxPy|. Questo equivale al calcolo del determinate di una matrice primale avente 4 elementi (ovvero 2 e Pz sulla diagonale e Px e Py sull'antidiagonale).
Osservazione 1. Nella equazione (*) di cui sopra avremmo anche potuto scrivere:
Osservazione 2. Dato che un numero dispari è anche uguale alla differenza tra un numero dispari ed un numero pari nell'equazione (**) di cui sopra, avremmo anche potuto scrivere:
Osservazione 3. Dal lemma di Chen si deduce subito che:
da cui
Osservazione 4. Come si può notare ogni numero primo risulta scrivibile come combinazione lineare di altri numeri primi.
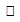
Esempi:
insieme di numeri primi disponibili per generare matricialmente altri numeri primi Γ = {2, 3}

con Γ = {2, 3, 5} mediante cui otteniamo la matrice:
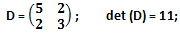
con Γ = {2, 3, 5, 11} da cui risulta possibile ottenere la matrice:
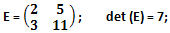
con Γ = {2, 3, 5, 7, 11} mediante cui otteniamo la matrice:
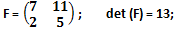
con Γ = {2, 3, 5, 7, 11, 13} da cui risulta ricavabile la matrice:

con Γ = {2, 3, 5, 7, 11, 13, 17} da cui risulta possibile ottenere la matrice:
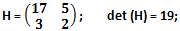
con Γ = {2, 3, 5, 7, 11, 13, 17, 19}
A questo punto notiamo che il 7 risulta generabile solo mediante una matrice generatrice semplice (per questo, attualmente, #(Ps) = 1). Un’ulteriore ricerca potrebbe evidenziare se esistono altri numeri primi non generabili mediante matrici primali assolute.
Andrebbe poi indagato anche l’andamento della cardinalità matriciale, ovvero il numero di matrici generatrici associabili alla generazione di ciascun numero primo.
Teorema 2. (Teorema sulla generazione matriciale di N). Un numero naturale può sempre essere calcolato come determinante di una matrice primale triangolare o di una matrice primale diagonale o di una primale. Se può essere calcolato solo come determinante di una matrice primale allora è primo.
Dimostrazione. Questo teorema nasce come conseguenza del Teorema fondamentale dell'aritmetica e del Teorema sulla generazione matriciale di P*. Inoltre sappiamo che data una matrice Q ∈ P*1,1 , det(Q) ∈ P*.
MATRICI PRIMALI GEMELLARI
Un sottoinsieme delle matrici primali è costituito dalle matrici primali gemellari, ovvero matrici T ∈ P*2,2 che presentano sulla diagonale il numero primo gemello maggiore e, sull’antidiagonale, il numero primo gemello minore.
Teorema 3. (Teorema sul determinante delle matrici gemellari). Sia data una matrice T ∈ P*2,2. Se T è una matrice gemellare allora il suo determinante è 24λT dove λT ∈ N.
Dimostrazione. Dato che ogni coppia di numeri primi gemelli maggiori di 3 si presenta nella forma (6λT + 1), (6λT - 1), con λT ∈ {1, 2, 3, 5, 7, ...} ⊂ N, una generica matrice primale gemellare T ∈ P*2,2 risulta così composta:

dove det (T) = (6λT + 1)2 - (6λT - 1)2 = 36λT2 + 1 + 12λT – 36λT2 – 1 + 12λT = 24λT
Corollario 1. Consideriamo ora la matrice gemellare fondamentale TΦ ∈ P*2,2 costituita da 5 e 7 ed il cui determinante è 24.
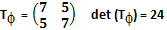
Dato che il determinante della matrice gemellare fondamentale TΦ è 24 possiamo allora scrivere:

Corollario 2. Dato che esistono matrici primali gemellari tali che λT ∈ P* ne consegue che esistono numeri primi scrivibili come:
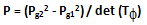
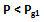
dove Pg1 = 6λT - 1 e Pg2 = 6λT + 1
Teorema 4. (Teorema sul determinante di una matrice prodotto di due matrici gemellari). Date due matrici gemellari T’, T’’ ∈ P*2,2 il det(T’T’’) è uguale a:
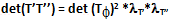
Dimostrazione. Per il lemma di Binet sappiamo che date due matrici E e S, il det(ES) = det(E)*det(S) per cui, dato che det(T’) = λT' * det (TΦ) e det(T’') = λT'' * det (TΦ), abbiamo che:
CONCLUSIONI E RINGRAZIAMENTI
In conclusione è mio profondo desidero ringraziare il Prof. Letterio Gatto ed il Prof.
Massimiliano Mattone del Politecnico di Torino per avermi sempre incoraggiato a proseguire nelle mie ricerche.


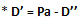
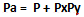
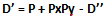
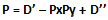
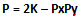
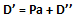

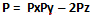
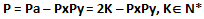
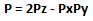







Uno studio originale che mette insieme molti concetti della matematica, dai numeri primi passando per alcuni teoremi riguardanti le matrici. Aspetti che forse potrebbero trovare spazio nella crittografia dei dati.
Ciao Maurizio,
in effetti quanto esposto in questi articoli potrebbe avere delle ripercussioni sulla matematica applicata…
Approfitto di questo interessante articolo per chiedere se tra gli autori/lettori c’è qualcuno esperto in crittografia RSA per eseguire alcuni test. Grazie in anticipo.
Gent.mo Marcello Colozzo,
la ringrazio molto del suo interesse verso i miei articoli.
A tal proposito vole chiederle se era possibile contattarla.
Ringraziandola in ogni caso
Le porgo
Distinti saluti
la mia email [email protected]