Algoritmi di compressione dati

La sempre maggiore disponibilità di interfacce per lo scambio dati, e le reti prese d’assalto con l’espansione dell’utilizzo dei dispositivi portatili, rende necessario realizzare condivisioni dati veloci ed efficaci, in grado di raggruppare nel più breve tempo possibile il maggior numero di informazioni. In questo testo analizzeremo perché è necessario comprimere i dati, e affronteremo le tecniche utilizzate per svolgere queste operazioni.

Quando si avvia una comunicazione, si cerca sempre di raggiungere una condizione in cui ogni singolo bit inviato è assolutamente necessario per la comprensione del pacchetto da parte del ricevitore; se poi i dispositivi impiegati sono wireless e a batteria, allora la richiesta nel comprimere diventa ancora più gettonata. Il risparmio nell’inoltro anche di un singolo bit per pacchetto, in applicazioni mobili alimentate da una sorgente interna facilmente esauribile, può, dopo ore di scambio di dati, risultare di enorme aiuto, in quanto permette al dispositivo un tempo di vita maggiore.

L’azione di comprimere dati è una tecnica ingegneristica che permette, fornito un pacchetto dati in ingresso, di diminuirne le dimensioni rendendolo maggiormente idoneo per il suo trasferimento. Questa tecnologia si impiega in tutti quei settori in cui sarebbe proibitivo trasmettere le informazioni a causa della mole di byte in gioco. Durante l’utilizzo del PC, spesso si lavora a propria insaputa con file compressi: visualizzando un immagine in JPEG, aprendo uno .zip, o semplicemente scaricando pagine da internet e facendo lavorare il modem ADSL. Si può tranquillamente affermare che la maggior parte dei dispositivi che comunica, svolge funzioni interne che permettono la riduzione della quantità di dati.

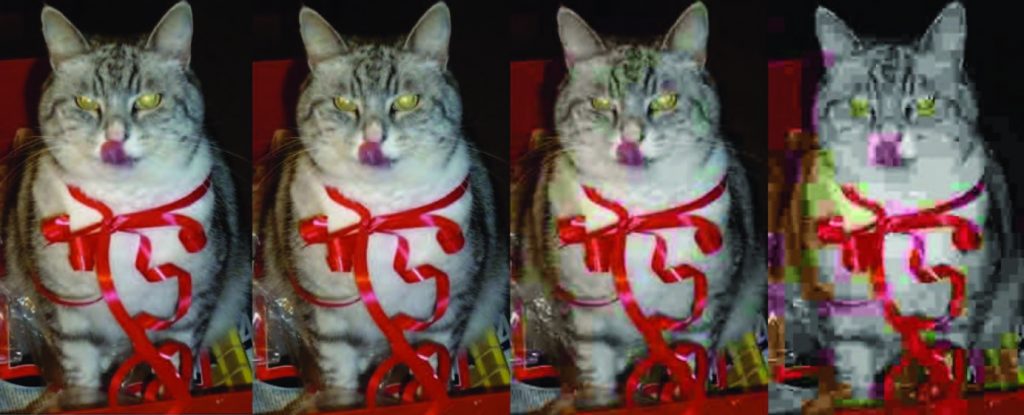
Figura 1: l‘immagine di sinistra rappresenta l’originale, un file di dimensioni 400X248 pixel e viene mantenuta tale per tutte e quattro le foto. Viene variata la qualità, obbligando il programma di grafica a comprimere rispettivamente al 10%, 85% e 95%.

Le due tipologie di compressione

Esiste un numero elevato di algoritmi differenti per ridurre i dati in gioco, alcuni proprietari e coperti da brevetti, altri gratuiti e sotto licenza open source, ma in ogni caso qualsiasi funzione viene catalogata in base ad un fattore molto importante: la perdita dei dati a se correlata. Qualsiasi persona, anche un non esperto in materia, si rende conto che per ridurre le dimensioni di un testo il metodo più semplice e veloce è l’eliminazione delle informazioni non strettamente necessarie, raggiungendo un punto in cui la cancellazione anche di un singolo valore può compromettere la comprensione da parte del ricevitore. Il modello appena descritto prende il nome di compressione dati lossy, o compressione a perdita di dati. Al giorno d’oggi, il linguaggio usato per esprimersi tramite sms, troncando, eliminando o sostituendo parti delle lettere dalle parole, può facilmente essere associato a questo sistema di compressione dati. Un messaggio di testo del tipo ”come stai, comunque oggi non sono andato dal dottore” può diventare brevemente “cm stai, cmq oggi nn sn andato dal dott.”. Ci sono situazioni in cui la perdita di informazioni non è contemplata, in cui la riduzione delle spazio occupato dal file, deve essere affidata ad un opportuna funzione che garantisca l’efficacia nella ricostruzione del pacchetto originale. Quando si sta lavorando con documenti di testo in formato .doc, o si ha semplicemente la necessità di raggruppare molti elementi in un singolo file, si dovrà impiegare un algoritmo di compressione dati lossless, ovvero senza perdite.

Gli algoritmi lossy

Le tecniche con perdita di informazione (lossy) permettono anche delle compressioni molto spinte, quindi un grande risparmio di risorse, a discapito però della qualità dell’immagine o dell’audio che si è voluto comprimere. Generalmente impiegate per diminuire lo spazio occupato nei file multimediali, mantenendo minima la perdita di qualità, il risparmio rispetto ad un compressione lossless è sempre decisamente apprezzabile.

Esempio di lossy

Visto il campo d’impiego di una compressione di questo tipo, il metodo più facile e veloce per rapportare pregi e difetti nell’utilizzo di una manipolazione lossy, sono le quattro immagini in Figura 1. Tutte e quattro le foto hanno una dimensione di 400X248 pixel, ma differiscono una dall’altra dalla quantità di compressione effettuata. La prima immagine, quella a sinistra è l’originale, per la grandezza in questione risulta molto definita e ingrandibile per l’individuazione di eventuali dettagli, ha una dimensione di 81,6 Kb. La seconda immagine utilizza un indice di compressione del 10%, mantiene le stesse dimensioni dell’originale, anche se per l’ingrandimento perde notevolmente in definizione. La dimensione, con una qualità ridotta di un decimo, risulta meno della metà dell’originale, 30,6 Kb. Alla terza immagine viene imposta una riduzione del’85%, e anche se ad occhio nudo si nota una leggera perdita e sgranamento, ingrandendo si riesce a percepire come i pixel diventino “quadratosi” e l’immagine è difficile da riconoscere. Una compressione di questo tipo porta la dimensione della figura a 6,1 Kb, ovvero a circa il 7% dello spazio occupato dall’originale. La quarta e ultima figura è un’immagine realizzata solo didatticamente, ma inutilizzabile nelle sue dimensioni in quanto risulta difficilmente distinguibile la rappresentazione. In questo ritratto viene imposto un indice di compressione del 95%, perdendo enormemente in qualità, ma guadagnandone rispettivamente in spazio occupato: 3,3Kb.

Le problematiche del lossy

Gli algoritmi lossy sono molto efficaci in tutte quelle applicazioni in cui si ha una conversione da analogico a digitale, nelle quali dei campionamenti imposti a determinati istanti di tempo realizzino il risultato finale. Nel caso specifico di un video composto da una serie di immagini, i campionamenti eseguiti nel sensore CCD della videocamera realizzano la serie di foto da visualizzare in rapida successione. Se di queste foto se ne elimina una ogni due, si vedrà come risulterà un video con spazio più contenuto, ma visualizzabile a scatti e quindi meno performante per l’utente finale. Tutti gli algoritmi con questo stampo puntano ad eliminare porzioni di dato per riuscire a diminuire sensibilmente lo spazio occupato dal file generato: più elevata è la percentuale di compressione e più elevata sarà la riduzione di valori apportata.

Gli algoritmi lossy d’utilizzo corrente

In questo breve testo non si riuscirà a trattare nel dettaglio il funzionamento dei singoli algoritmi, ma un accenno per portare il lettore a conoscenza dei pregi e i difetti di un a codifica lossy sicuramente non sarà snobbata. Ogni algoritmo è frutto di un lavoro intellettuale da parte di matematici, programmatori, studenti o anche appassionati, quindi a fronte di ciò può essere coperto o meno da brevetto. Le funzioni di compressione a perdita di dati, svolgono principalmente il loro lavoro con immagini, video e audio, un breve elenco:

MP3: il formato di compressione dati lossy per eccellenza, quello che almeno una volta tutti hanno incontrato nella propria carriera di amante della musica, è l’MP3. MP3 è l’acronimo di MPEG 1 Layer 3, ed è particolarmente efficace per la compressione di audio senza incappare in una perdita di qualità troppo Partendo da un file audio non compresso, per esempio un .wav, che ripropone la campionatura esatta della forma d’onda del segnale audio, l’MP3 eseguirà una prima scrematura, eliminando tutte quelle frequenze, alte o basse, impercettibili per l’orecchio umano. Il secondo passaggio provvederà a dividere in parti uguali ogni singola parte dello spettro, eliminando e accorpando le porzioni consecutive di valore simile. Una compressione di questo tipo è in grado di portare da un file .wav di dimensione 50Mb ad un file .mp3 di 5Mb, senza che si possa percepire una considerevole differenza nell’audio in uscita;
JPEG: così come avviene per l’audio con l’MP3, anche nelle immagini viene adottato un meccanismo software per renderle di dimensioni contenute, senza andare a diminuire sensibilmente la qualità della foto stessa. Il Joint Photographic Experts Group, nome della commissione che ha definito le specifiche per la realizzazione del JPEG, ha analizzato come questo algoritmo di compressione risulti maggiormente indicato con immagini ad elevato numero di colori, a toni di grigio o disegni molto sfumati, rendendosi invece alquanto inadeguato per l’impiego in tutte quelle immagini in cui compaiano pochi cambi di colore, per esempio nei “cartoni animati”. Il JPEG riduce la quantità di dati, sfruttando le limitazioni dell’occhio umano: se si trovano due pixel con minima variazione di luminosità vengono conservati, mentre se si analizzano due punti con minima variazione di colore se ne conserverà uno solo;
MPEG: la rapida diffusione delle tecnologie video digitali, con una qualità di risoluzione sempre maggiore, ha richiesto l’implementazione di tecniche per la compressione video nel ramo delle telecomunicazioni. Un ottimo algoritmo che riesce a ridurre efficacemente video e audio senza intaccare sostanzialmente la qualità, rendendo i dati facilmente gestibili e idonei alla condivisione, è l’MPEG. l‘MPEG, o Motion Picture Espert Group, è un gruppo specializzato nella ricerca audio-video, i quali hanno definito le specifiche dello standard in uso. Fin dall’inizio della formazione di questo pool di esperti, il lavoro si è indirizzato su tre fronti, MPEG-1, MPEG-2 e MPEG-4. Ciò per garantire all’utenza la possibilità di una vasta scelta in termini di mole di dati o qualità. L’MPEG in di per sè non definisce un nuovo sistema per comprimere i dati, ma raggruppa in se due standard facendoli operare insieme: MP3 per l’audio e il JPEG per il video.

Gli algoritmi lossless

In pacchetti che nascono digitali, e quindi in cui ogni singolo bit è necessario per la comprensione del pacchetto, è impossibile utilizzare una compressione di tipo lossy. Gli eseguibili, i file di testo, i file di configurazioni, sono tutte informazioni che devono viaggiare inalterate, modificate sotto altre forme, convertite per essere trasmesse con maggiore facilità, ma sempre ed in ogni caso dovranno raggiungere il ricevitore nella loro forma iniziale.

Esempi di lossless

Per gli algoritmi lossless un esempio lampante, che permette di comprendere efficacemente il funzionamento reale di un sistema di questo tipo, è difficile da presentare. Ogni funzione di compressione si differenzia dalle altre per i cicli, la velocità e il rapporto pacchetto in uscita su pacchetto in ingresso, quindi due differenti algoritmi lanciati nel medesimo dato difficilmente avranno le stesse prestazioni. La più semplice delle funzioni per ridurre la quantità di informazioni in gioco in una sequenza di dati, consiste nella sostituzione delle ripetizioni e degli spazi in eccesso, con informazioni che seppure diverse raggruppano il dato. Si consideri un pacchetto del tipo:

4442845 6222222000099668

si può facilmente analizzare come siano presenti delle ripetizioni, dei caratteri e degli spazi che raggruppati farebbero risparmiare spazio, e quindi renderebbero la comunicazione più veloce. Il pacchetto in esame quindi può diventare:

34 2845 6s 6 62402926 8

Siccome si hanno delle ripetizioni ad inizio del vettore, si comincia associando i 444 con il numero 34, ovvero: il primo numero corrisponde al moltiplicatore e il secondo al valore ripetuto, perciò 3 volte 4 = 34. Ogni spazio indica un cambiamento di fronte, informando che la porzione di dato seguente dovrà essere interpretata alternativamente o come raggruppamento o come valore in se stesso. Nel caso specifico, all’inizio compaiono tre ripetizioni del numero 4, ma a seguire si trova il valore 2845, che convertito in valori di ripetizione corrisponde a 12181415, poco performante e sconveniente. Per evitare queste situazioni è preferibile lasciare isolati i valori singoli, dunque scelto di cominciare il pacchetto con le ripetizioni, il primo spazio indica che i numeri che seguono non sono stati convertiti e quindi bisogna riportarli così come sono, il secondo spazio informa nuovamente della presenza di ripetizioni, e così via per tutta la lunghezza del messaggio.

Le problematiche del lossless

Le funzioni di tipo lossless, anche se immuni dalla perdita di informazioni, non sono però esonerate da problematiche funzionali. In primo luogo, i sistemi che adottano questi algoritmi devono essere interfacce molto veloci, in quanto la potenza di calcolo per la conversione viene messa spesso sotto stress. In secondo luogo non garantiscono al 100% una riduzione effettiva del pacchetto in gioco. Ripreso in esame il codice presentato nel paragrafo qui sopra, si vede come se il dato da comprimere è formato prevalentemente da valori che non si ripetono, l’efficacia della funzione presentata tende bruscamente verso lo zero, non offrendo vantaggi nell’impiegare tale sistema. Nel caso specifico, preso:

346728 2873928 34828347

il valore generato sarà:

346728s2873928s34828347

dove le “s” indicano gli spazi nell’informazione.

Gli algoritmi lossless d’utilizzo corrente

Posti a confronto con i lossy, i lossless sono algoritmi più complessi e difficili da realizzare, ma allo stesso tempo coprono interfacce impiegate nei settori più disparati. Generalmente ogni campo d’impiego ha tipologie di dati differenti le une dalle altre, e per questo vengono spesso adattate o scelte funzioni di compressione maggiormente prestanti al lavoro in opera. La maggior parte dei lossless, chi più e chi meno, analizza il pacchetto alla ricerca di ridondanze, convertendo le ripetizioni eventualmente individuate con pacchetti rappresentanti gli stessi valori. Gli algoritmi impiegati maggiormente sono: compressione secondo Huffman, algoritmi LZ, trasformata di Burrows-Wheeler e codifica aritmetica.

Compressione secondo Huffman

Considerando l’articolo che si sta leggendo, scritto in italiano, ci sarà sicuramente una maggiore ripetizione di “e” e di “a” rispetto a “z” e “x”. L’algoritmo di Huffman svolge la compressione con i seguenti passaggi:

si esegue una statistica per determinare le ripetizioni dei caratteri;
si crea un codice prefissato;
si raggruppano i simboli in ordine di occorrenza;
si combinano i due simboli con occorrenza minore, creando un nuovo nodo (che avrà occorrenza pari alla somma delle occorrenze dei due) e mettendoli come figli;
si ripete il processo fino a non aver ottenuto un albero;
si sostituiscono le stringhe di bit che rappresentano i caratteri con i corrispettivi;
si salva il file aggiungendo (come intestazione) il codice calcolato.

Un algoritmo di questo tipo è sicuramente efficace ma complesso da implementare nei microcontrollori, e in aggiunta per avere un rapporto consistente di compressione tra messaggio in ingresso e messaggio in uscita, si dovrà utilizzare un pacchetto di dimensioni elevate, in modo che lo studio statistico sia di rilevante impatto per l’individuazione delle ripetizioni.

Algoritmi LZ

La famiglia di algoritmi LZ, anche se presente in molte varianti, differenti nel rendimento, sfrutta essenzialmente la sostituzione del testo. Idonea per comprimere molti tipi di dati differenti: immagini, audio e file di testo, le funzioni LZ eseguono un’indagine statistica del testo tenendo conto della posizione e della lunghezza di ogni singolo pacchetto, in modo che se questo fosse individuato nuovamente all’interno del messaggio da comprimere, sarà sostituito semplicemente con la posizione del dato equivalente. Questo schema può anche essere reso più efficiente in termini di mole di dati ripetendo N volte, a discapito però della velocità di conversione. Tutti i metodi di questo gruppo sono basati sull’algoritmo LZ77. Un raffinamento di questo algoritmo è LZSS, algoritmo sviluppato nel 1982 da Storer e Szymanski.

Trasformata di Burrows-Wheeler

La trasformata dai Burrows-Wheeler non è un vero e proprio algoritmo di compressione dati, ma è un efficiente funzione per ordinare un pacchetto in modo che i caratteri uguali si trovino gli uni attigui agli altri. Si è analizzato come il primo passo per effettuare una compressione è l’eliminazione, o la sostituzione, delle ripetizioni. Spesso però accade che in alcuni pacchetti siano presenti caratteri identici, ma disposti distanti gli uni dagli altri, e quindi impossibili da raggruppare in un pacchetto del tipo indice di ripetizione/dato (vedi paragrafo Esempi di lossless). La trasformata di Burrows-Wheeler non fa altro che eseguire dei cicli di permutazione al pacchetto, fino a fargli raggiungere una condizione in cui i valori uguali si trovano disposti in successione.

Codifica aritmetica

La codifica aritmetica è molto simile all’algoritmo di Huffman presentato all’inizio del paragrafo corrente. Partendo dal presupposto che alcuni simboli compaiono in un testo maggiormente di altri, a differenza di Huffman che associa ad ogni carattere il rispettivo valore, la codifica aritmetica associa ad ogni porzione di messaggio un valore di lunghezza inferiore al blocco in questione. Così facendo mentre Huffman va a sostituire ogni carattere con il rispettivo dato binario, nella compressione aritmetica ogni blocco va mutato con un valore che lo rappresenta.

Conclusioni

La compressione dati è un ramo delle telecomunicazioni molto vasto e complesso, e ogni applicazione, seppure leggermente differente, impone l’utilizzo di algoritmi completamente diversi per raggiungere risultati elevati. Maggiore è la complessità dell’algoritmo da impiegare, maggiore dovrà essere la velocità del controllore adibito alla compressione. Per queste ragioni, la maggior parte delle volte si tende a tralasciare un argomento così delicato, in quanto adottare una funzione che riduca il dato da trasferire a discapito delle prestazioni del sistema stesso non è sicuramente un buon compromesso.