Riprende il nostro corso di programmazione su ARM, come vi avevamo accennato la volta scorsa con una breve parentesi matematica dalle notevoli applicazioni pratiche. Si tratta di un approfondimento tematico su uno degli argomenti più importanti per tutti coloro che si occupano di elettronica e di telecomunicazioni: la Trasformata di Fourier. La conoscete di sicuro ma probabilmente non l'avete mai vista impiegata in questo modo. Facciamo un test preliminare: sapete che cos'è l'algoritmo Radix-2? Curiosi? Speriamo di sì perché questa nuova puntata sta per cominciare.
La Trasformata di Fourier è un'operazione matematica che viene largamente impiegata nel campo dell'ingegneria, specificatamente da tutti coloro che lavorano con segnali e che hanno la necessità di trattarli opportunamente. Il presupposto teorico di questa operazione di trasformazione, che associa ad una funzione reale di variabile reale, leggasi il tempo, una nuova funzione definita, però, questa volta, in funzione delle frequenze, è che sia possibile, teoricamente, scomporre, o meglio ricomporre, un qualunque segnale nota che sia la serie delle infinite armoniche che lo compongono.
Un qualsiasi segnale reale, specie se non periodico, magari il risultato di un processo aleatorio, anche se non può essere descritto da una funzione elementare, può comunque risultare da una sovrapposizione di infiniti contributi sinusoidali.
Come tutti gli ingegneri sanno, però, "infinito" è sinonimo di approssimazione, non foss'altro perché non è fisicamente possibile descrivere un numero così grande di contributi. Con l'avvento dell'era digitale tale considerazione ha assunto un'importanza ancora più cruciale dal momento che per poter descrivere un segnale, già noi, abbiamo necessità di fare delle approssimazioni ma perché possa essere una macchina, un computer, con la sua finita precisione, a descrivere una forma d'onda è necessario fare delle approssimazioni molto forti.
Il grado di approssimazione che si richiede rende sostanzialmente critico decidere subito quale sia la precisione che vogliamo richiedere e quella che possiamo tollerare.
Ma, prima di addentrarci in questo genere di considerazioni, è necessario ricordare qualcosa in più su,la trasformata di cui stiamo parlando.
La Trasformata di Fourier Discreta
Come dicevamo, la precisione con la quale è possibile rappresentare i numeri all'interno di un calcolatore non è infinita e questo naturalmente significa che un numero reale non potrà essere rappresentato con tutte le cifre significative di cui è costituito.
Questo vale tanto per i numeri quanto per i valori dei segnali, per esempio. Ed ecco per quale motivo la Trasformata di Fourier, dapprima definita su tutto l'insieme dei numeri reali, deve vedere una discretizzazione apportata all'insieme di definizione che la trasforma in DTFT, ovvero Discrete Time Fourier Transform. Naturalmente, però, proprio per effetto della precisione finita, la trasformata ha necessità di essere discreta anche nelle ampiezze cioè nel suo codominio il che la fa diventare Discrete Fourier Transform. Cioè siamo passati da una funzione reale di variabile reale ad una funzione discreta reale di variabile reale ma a valori discreti.
Si potrebbe, in linea del tutto teorica, implementare questa trasformata così com'è ma purtroppo, in realtà, questa non è la scelta migliore da farsi. La soluzione ideale è quella di creare degli algoritmi ad hoc che fungano allo scopo di implementare la trasformata ma ottimizzandone sia le procedure di calcolo sia la quantità di memoria occupata durante le operazioni. Ed è proprio con queste premesse che nasce la Fast Fourier Transform, altrimenti nota con l'acronimo FFT.
Si tratta, dunque, di una tecnica matematica che permette la trasformazione di segnali digitali definiti nel dominio del tempo in rappresentazioni definite nel dominio della frequenza delle ampiezze delle singole componenti spettrali.
Esiste un altro modo per guardare a questa trasformazione ed è prettamente analitico: si tratta di un metodo per trasformare calcoli di tipo integro differenziali in operazioni algebriche, ovvero somme e prodotti. Il vantaggio? È ovvio: sono più semplici da fare! E se si tratta di grandezze tutto sommato comunque elementari, è anche possibile non dover ricorrere all'utilizzo di un calcolatore per risolvere questi stessi problemi. Un bel vantaggio, non trovate?
Per questi ottimi motivi, la FFT, come annunciato in precedenza, è una delle più importanti operazioni, nonché argomenti, trattate da tutti coloro che operano nel campo del Signal Processing.
La sua importanza, come qualcuno saprà e come certamente è fondamentale ribadire, non si applica ad un caso specifico ma a tante casistiche diverse tra cui l'ambito che vedremo oggi ovvero le misurazioni e le applicazioni relative. Ciò nondimeno possiamo lavorare per fare riconoscimento vocale oppure codifica digitale di segnali acustici o ancora la rilevazione delle vibrazioni, filtraggio, la risoluzione delle equazioni differenziali alle derivate parziali e così via dicendo.
Per capire meglio di che cosa stiamo parlando è importante chiarire meglio che cosa vuol dire "discreto".
Ne abbiamo già dato una definizione ma adesso lo vedremo applicato.
Il fatto che si chiami "discreta" identifica una sequenza di istanti temporali definiti ovvero il tempo non è più una variabile reale ma assume solo alcuni valori reali. D'altronde questo è evidente: un processore funziona ad una determinata frequenza e genera singoli istanti, eventi, di clock. In corrispondenza di questi singoli istanti sono definite singole specifiche ampiezze.
Ciò significa che la variable d'ingresso alla trasformata è una sequenza finta di numeri reali (che possono anche essere complessi).
Come dicevamo, c'è una relazione tra la DFT e la FFT: la prima si riferisce alla trasformazione matematica o alla funzione indipendentemente da come questa venga calcolata. Nel secondo caso, invece, ci riferiamo ad una specifica famiglia di algoritmi che permettono l'implementazione della DFT all'interno del calcolatore.
La DFT viene definita come segue:
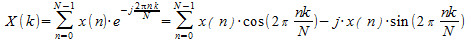
in cui abbiamo indicato con X(k) il risultato della trasformazione, x(n) le variabili di ingresso che altro non sono se non i campioni discreti del segnale di ingresso cioè il risultato del campionamento del segnale e con "j" che l'unità immaginaria.
Ciascun elemento che fa parte di questa equazione definisce l'equazione di una sinusoide complessa di data frequenza e fase. kF0 è la frequenza multipla della fondamentale ed è proprio quell'indice, che varia, a definire quali sono le armoniche prese in considerazione.
La trasformazione è ingestibile perché si tratta di un'operazione lineare e pertanto scriviamo la IDFT (Inverse DFT) come:
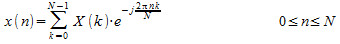
Dal punto di vista computazionale, calcolare tutti gli N valori delle componenti di frequenza richiede un totale di NxN moltiplicazioni complesse ed N(N-1) somme tra numeri complessi.
Si può fare di meglio.
L'implementazione della FFT
Quando lavoriamo con il calcolatore abbiamo necessità di essere veloci, occupare poca memoria ma soprattutto restituire il più velocemente possibile il risultato corretto, salvo aver fatto errori di valutazione. Una volta che abbiamo verificato di aver compreso come funziona la trasformazione, la sua implementazione all'interno del calcolatore è abbastanza semplice. Poniamo:
grazie alla quale rappresentazione possiamo ridefinire la DFT e la IDFT come segue:
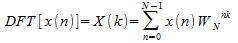
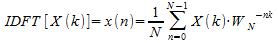
Per migliorare
l'efficienza dell'algoritmo, è indispensabile ricordare alcune delle proprietà di cui gode Wn, tra cui la simmetria rispetto all'asse dello spettro del segnale e la periodicità, che discende dal fatto che si tratta di un segnale sinusoidale, ovviamente.
L'idea alla base del metodo di implementazione è quello di decomporre la DFT in sequenze elementari. Se questo è possibile, la sequenza dei campioni definiti nel dominio del tempo di lunghezza N diventerebbe un insieme di p sequenza lunghe ciascuna N/p che, singolarmente, sarebbero più semplici da calcolare perché ci sarebbero meno operazioni da compiere.
Ciò nondimeno anche l'identificazione di quante sequenze richiede un certo metodo ed esiste una strategia che definisce questo genere di passaggio matematico.
Possiamo dividere semplicemente la sequenza in due sequenze oppure in più di due sequenze ma in ogni caso dovremo tener conto del fatto che la sequenza di partenza può essere pari o dispari e quindi ci potremmo trovare nella situazione in cui:
- a(m)=x(2m), nel caso pari;
- b(m)=x(2m+1), nel caso dispari;
tutto questo avendo definito 0<m<N/2.
Questo processo di divisione della sequenza nel dominio del tempo in un numero di campioni pari e dispari conferisce all'algoritmo il nome di "Decimation In Time" (DIT). Questo perché la decimazione avviene per un fattore due. Ecco quindi che l'implementazione del metodo prevede successive divisioni per due fino alla scomposizione più elementare. Ecco da dove viene fuori il nome "Radix-2".
Ora che abbiamo capito il concetto, trasformiamo la DFT in una DFT decimata per ottenere la seguente espressione:
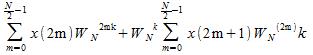
Ciò rappresenta la DFT a N/2 punti delle due sequenze rispettivamente. Pertanto possiamo riscrivere il tutto come segue:
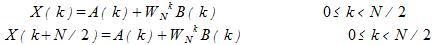
in cui possiamo anche fare delle supposizioni dal momento che la proprietà di periodicità ci permette di restringere il numero di campioni di nostro interesse a solo mezzo intervallo, ovvero da 0 a N/2.
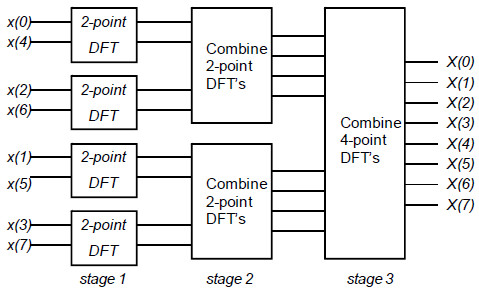
Il risultato dell'espressione ricorsiva è proprio la FFT DIT Radix-2. Questa struttura ci permette di identificare ciascuna sequenza costituita da N/2 punti in una sotto sequenza pari ed una dispari e questo processo viene ripetuto ancora e ancora fino a quando non succede che si riduce il tutto allo schema che segue
Va osservato che il costo computazionale dell'intera operazione può essere semplicemente calcolato come 2^3=8, o se volete invertendo il tutto tramite l'uso dei logaritmi. In linea generale, per una FFT ad N punti, quindi, l'algoritmo decompone la DFT in un numero di strade di pari alla logaritmo in base due di N.
Cosa serve per farla?
Adesso che sappiamo di che cosa stiamo parlando, cerchiamo di capire meglio che cosa dobbiamo fare per ottenere esattamente questo risultato. Si intuisce che, indipendentemente dal numero di stadi che andremo ad implementare, le caratteristiche di ciascuna divisione devono essere esattamente identiche per ottenere un risultato valido.
Se abbiamo una sequenza di 8 punti in ingresso la rappresentazione decimale vedrà i numeri rappresentati da 0 a 7. Il numero binario equivalente sarà il risultato della conversione in binario del numero decimale per cui 0 sarà 000, 1 sarà 001 e così via dicendo.
Quando dobbiamo calcolare la rappresentazione invertita sostanzialmente otterremmo numeri speculari per cui 1 sarà 100 e 6 verrà rappresentato da 011 (che di solito, invece, indica il 3). Questo primo stadio permette di riordinare la sequenza di ingresso; questo vuol dire che questo algoritmo ha bisogno di un ordinamento inverso, cioè quello che abbiamo appena visto: il bit più significativo diventa l'ultimo e l'LSB prende il posto dell'MSB.
L'uscita di ciascun percorso tra quelli visti in precedenza può essere posizionata all'interno della stessa locazione di memoria dalla quale sono stati indirizzati i dati di ingresso; questa osservazione è fondamentale perché questo algoritmo può essere eseguito senza richiesta di ulteriore memoria rispetto a quella necessaria per memorizzare il dato.
Ma tutto questo risulta davvero possibile soltanto se si effettua una operazione di finestratura efficace. Si suppone, infatti, che il segnale sia periodico in ciascun blocco. Questo vuol dire che si ripete uguale a se stesso ogni volta che termina il suo periodo. Naturalmente questo è un caso abbastanza raro perché segnali perfettamente periodici è difficile che siano frequenti e anche se fosse periodico è possibile che abbia un periodo sconosciuto (che di solito è la soluzione per segnali che non sono periodici ovvero si suppone che il periodo sia molto lungo, tipicamente infinito). Quando viene effettuata la trasformata di un segnale non periodico, sussistono dei fenomeni di perdita per quanto riguarda le componenti frequenziali che devono essere necessariamente scartate visto che il segnale non può essere osservato per intero (non abbiamo tempo infinito da aspettare! Inoltre, se lo avessimo, dovremmo poi spendere altro infinito tempo per l'elaborazione…).
Per risolvere questo problema è una buona soluzione selezionare un certo numero di campioni dell'ingresso per renderli periodici; questo può essere fatto con alcune funzioni di finestratura canoniche oppure realizzandone una ad-hoc. Tra le tante abbiamo Bartlett, Blackman, Bessel e così via dicendo.
Se consideriamo il risultato dello spettro dopo l'applicazione della funzione di finestratura, quindi sostanzialmente del filtro (tanto per chiamarlo col suo nome), abbiamo delle differenze nella sagomatura spettrale rispetto al segnale "puro".
Quindi sebbene l'operazione di filtraggio che stiamo facendo alteri la struttura dell'intero segnale, abbiamo la necessità di utilizzarla. In linea del tutto teorica, allora, la soluzione migliore è il filtro passa basso ideale, ovvero il filtro rettangolare. Sta proprio, ancora una volta, nell'aggettivo "ideale" il motivo per cui questo non può davvero succedere: il filtro ideale taglia esattamente una frequenza. Ma naturalmente questa esatta precisa selezione non è possibile. Come sappiamo tutti i filtri decadono più o meno velocemente a seconda del loro ordine e quindi propongono attenuazioni progressive delle componenti frequenziali indesiderate.
Per effettuare la rilevazione del periodo è possibile utilizzare delle tecniche di rilevazione dello zero, ovvero ZCD (Zero Crossing Detection). La spiegazione la potete trovare nella prossima figura:
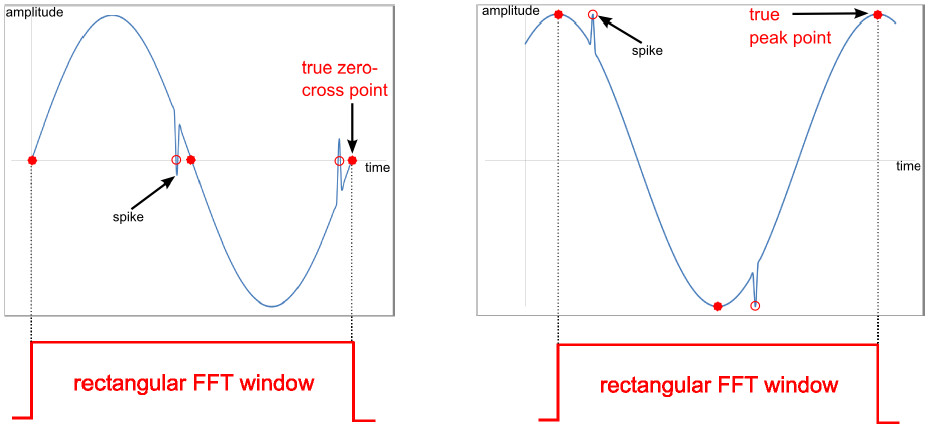
Nel momento in cui il segnale attraversa lo zero, non c'è tensione ai capi del circuito; se abbiamo supposto che la forma d'onda è sinusoidale, ci aspettiamo che in un periodo l'attraversamento dello zero accada almeno due volte. Questa considerazione potrebbe già essere sufficiente per farci ricavare il valore del periodo.
Un comparatore interno all'microcontrollore potrebbe essere la soluzione ideale per rilevare esattamente questo fenomeno. Il tempo che intercorre tra l'attraversamento dello zero ed il successivo è misurato da un timer. Applicando la finestra rettangolare si può ottenere l'operazione di filtraggio così come l'avevamo pensata.
Va fatto notare che l'operazione di finestratura eseguita sui dati campionati non causa fenomeni di perdita come nel caso analogico; vi risulta chiaro il perchè?
Gli spike che trovate rappresentati in figura altro non sono che fenomeni di attraversamento spuri. Dobbiamo supporre che questi possano essere contributi di rumore che interferiscano sul normale svolgimento del processo casuale che stiamo analizzando. Sarà necessario non confondere questi valori con contributi significativi.
La FFT Radix-2 utilizza dunque degli artifizi davvero interessanti che permettono di fare la stessa identica cosa della DFT ma in meno tempo. Il rapporto tra il costo computazionale della DFT e quello della FFT è pari a
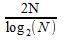
dal quale rapporto si può intuire quale sia la convenienza in funzione del valore di N.
Ok, ma le misure che c'entrano?
In effetti è proprio quello l'argomento di oggi e ci arriviamo tra un attimo.
L'implementazione nelle misure di potenza richiede l'utilizzo di numeri complessi, perfettamente compatibili con la natura della trasformata. Questo sostanzialmente si esplica nell'utilizzo dei fasori, un concetto che sicuramente tutti voi avete ben chiaro ma che riprendiamo qui di seguito.
Se definiamo un piano cartesiano che abbia sulle ascisse la parte reale di un numero complesso mentre sull'ordinata la parte immaginaria, possiamo sempre definire un vettore che parta dall'origine degli assi cartesiani e che abbia modulo, direzione e verso tali da congiungersi con il punto generico di nostro interesse tale per cui si definiscono
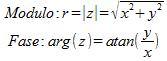
La fase rappresenta l'angolo formato dal vettore rispetto all'asse delle ascisse.
È noto che grazie al modulo ed alla fase si può descrivere completamente un generico numero complesso.
Nell'ambito dell'ingegneria elettrica, ma anche elettronica, talvolta è utile studiare le grandezze quali tensione e corrente, in funzione non già del loro valore istantaneo ma piuttosto del valore assunto in un determinato intervallo di tempo. Questo vale anche quando la grandezza elettrica sia stata acquisita, campionata e debba essere sottoposta ad un processo di trasformazione. Pensiamo a segnali in corrente alternata ma anche ad alcuni segnali in corrente continua che magari provengano da un'elaborazione oppure da un adattamento precedenti. In qualsiasi caso noi siamo, sul piano complesso, il piano di Gauss, di cui abbiamo appena parlato, queste grandezze possono essere rappresentate.
Ciò nondimeno esiste il valore quadratico medio, Root Mean Square o RMS, e questa figura di merito ci permette di valutare le grandezze elettriche in oggetto in qualità di valori efficaci anche in intervalli temporali lunghi.
A cosa può servire tutto questo?
Per esempio quando parliamo di
UPS. Se parliamo di potenza derivante da correnti e tensioni alternate, ci sono tre componenti fondamentali:
- la potenza reale (indicata con P), che viene misurata in W;
- la potenza apparente (indicata con S), che viene misurata in VA;
- la potenza reattiva (indicata con Q), misurata in VAr.
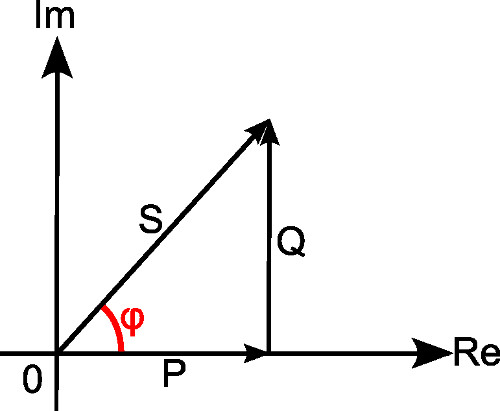
Queste tre componenti vengono disposte esattamente come segue
in cui l'angolo evidenziato rappresenta la fase della tensione rispetto alla corrente ovvero il loro mutuo sfasamento. La potenza complessa viene definita come
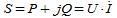
U è un vettore e quindi è costituito da parte reale e parte immaginaria ed altrettanto vale per il vettore associato alla corrente; possiamo sempre esprimere la potenza complessa in termini di fasori. Questo è fondamentale perché sono proprio queste le grandezze con le quali andiamo a lavorare quando effettuiamo la trasformazione FFT. Per questo motivo possiamo scrivere che
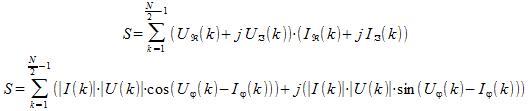
in cui vengono evidenziate le parti reali ed immaginarie della potenza complessa raccolte e raggruppate in maniera da rendere evidenti i vari contributi.
Rispetto alle proprietà della trasformata di cui abbiamo parlato ci sono due semplificazioni che vengono utilizzate per la rappresentazione dell'equazione.
Grazie, quindi, alla simmetria dello spettro vengono utilizzati soltanto la metà dei campioni;
ci si aspetta che non ci sia offset di tensione nella fondamentale ed infatti esso non compare.
La potenza apparente totale può anche essere calcolata come il valore quadratico medio della tensione e della corrente come:
Quindi, praticamente?
Che cosa vuol dire tutto questo? Che applicazioni pratiche ci sono? Come si può fare davvero tutto questo con le mani?
In C, tanto per iniziare.
E dando uno sguardo al seguente diagramma a blocchi

(fai click sull'immagine per ingrandirla)
FFT computing e power computing sono le due funzioni basilari della libreria "metering" che viene utilizzata oggi in diversi strumenti di misura. Ecco alcuni manuali di riferimento:
- DRM121, che descrive le applicazioni basate su MCF51EM256;
- DRM122, che descrive le applicazioni basate su MK30X256;
- Design Reference Manual, che descrive le applicazioni basate su MKM34Z128.
Cominciamo con la descrizione dell'API. Ci sono sostanzialmente, al suo interno, due funzioni principali che sono FFT_radix2 e PowerCalculation i cui nomi risultano essere auto esplicativi. La prima delle due accetta degli argomenti in ingresso che sono relativi al numero di campioni, ai singoli campioni e poi lavora sui risultati mentre la seconda funzione lavora con parametri quali tensioni, correnti e potenze.
Su ARM Cortex-M0+ le dimensioni del codice per le due funzioni sono pari, rispettivamente, a 514 byte e 706 byte.
L'uscita della funzione FFT sono dati in formato cartesiano in cui sia la parte reale sia la parte immaginaria hanno una profondità di 32 bit. La dichiarazione prevede l'inclusione dell'header file ed il seguente codice:
#include “fft2.h”
void FFT_radix2(unsigned short n,long input[N_SAMPLES],ComplexFFT result[N_SAMPLES])
in cui sono evidenti gli argomenti che sono dati senza segno con profondità a 16 bit oppure con segno a 32 dipendentemente dal fatto che si tratti del numero di campioni per periodo del segnale in ingresso piuttosto che dei dati veri è propri. Per quanto riguarda l'uscita, come dicevamo, si tratta di dati con segno della profondità di 32 bit che rappresentano la parte reale e la parte immaginaria.
La funzione che permette il calcolo della potenza, invece, viene dichiarata come segue:
#include “metering2.h”
void PowerCalculation (long voltage[N_SAMPLES], long current[N_SAMPLES], [...]
[...] Power_Vector *powers, unsigned long mU[MAX_FFT_SEND], [...]
[...] unsigned long mI[MAX_FFT_SEND])
che lavora con argomenti che sono, in ingresso, correnti e tensioni, numeri a 32 bit con segno di dimensione assegnata. In uscita, invece, ci sono numeri senza segno a 32 bit che rappresentano le ampiezze di tensioni e correnti ma anche cifre di potenza, le stesse di cui abbiamo parlato e che abbiamo indicato in precedenza, che sono con segno a 64 bit (per quanto riguarda la potenza attiva e per quella reattiva) oppure senza segno a 64 bit (potenza apparente) o a 32 (valore quadratico medio della tensione). Lo sfasamento viene restituito grazie ad un numero con segno a 32 bit.
E funziona tutto ciò?
Direi proprio di sì! Però dobbiamo valutare come, quanto. Nello specifico, quanto velocemente? Abbiamo finora parlato di velocità, di peso computazionale... È arrivato il momento di vedere se la libreria funziona davvero.
Come dicevamo, anche grazie all'elenco che vi abbiamo riportato, questo genere di libreria può essere utilizzato su differenti piattaforme con l'evidente risultato che i requisiti di calcolo possono essere rispettati in ogni caso ma naturalmente le performance potrebbero essere differenti.
In particolare si è visto come, al variare del numero di campioni che entrano a far parte della rappresentazione FFT del segnale, il carico computazionale, sia in termini temporali sia in termini di cicli di esecuzione, cambi sensibilmente. Fissata che sia la frequenza operativa, pari a 47,9 MHz, in un'architettura ARM CORTEX-M0+, abbiamo un minimo di 8 campioni che corrisponde ad un tempo di esecuzione delle operazioni di 0,24 ms. Questo, in cicli, si traduce in 11.513.
Quando i campioni diventano 16, il tempo passa 0,55 ms ed il numero di cicli a 26.384.
Se si arriva a 128 campioni il tempo di esecuzione è pari a 5,36 ms ed il numero di cicli arriva addirittura a 257.131.
Concludendo
Abbiamo scoperto oggi che esiste un modo per trasformare un'ottima architettura in una piattaforma per il metering ottimizzata per sfruttare tutta la potenza connessa con una delle operazioni matematiche più interessanti, ovvero la Trasformata di Fourier. Naturalmente questa tecnica presenta, come tutte, vantaggi e svantaggi. Tra gli aspetti più interessanti per cui prendere in considerazione quanto detto fino a questo momento ci sono la precisione con la quale l'energia, attiva e reattiva, viene trattata. Inoltre, il numero di misure restituisce un quadro completo dell'energia in gioco. Altro fattore fondamentale è la possibilità di valutare la Total Harmonic Distortion (THD).
Parlando di svantaggi, invece, non possiamo non notare che l'alto costo computazionali su microcontrollori impone l'utilizzo di un'architettura comunque avanzata (non a caso ne parliamo all'interno di un corso su ARM Cortex-M0+).
Quali sono le possibili applicazioni? Per esempio contatori che lavorano su impianti fotovoltaici o consumo elettrico di dispositivi ad alta tensione, gestione e controllo di impianti trifase. Le possibilità sono davvero notevoli.
Adesso è proprio giunto il termine della puntata. Vi ricordo di utilizzare i commenti per qualunque segnalazione, dubbio o domanda relativa a questa o alle altre puntate. Nella prossima, ed ultima, ormai, del corso, vi faremo vedere altro all'interno di CodeWarrior, torneremo mettere le mani sulla scheda perché di programmarla non abbiamo ancora finito. Alla prossima.
Per ulteriori informazioni potete scrivere a questa email: [email protected]

Ti potrebbe interessare anche:
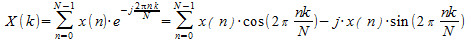
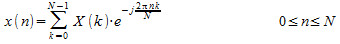
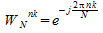
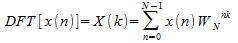
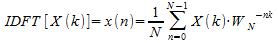
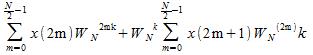
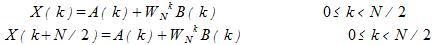

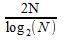
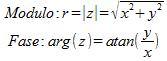
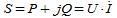
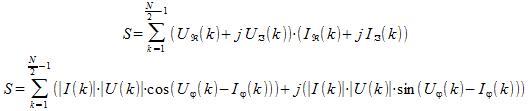
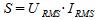








Complimenti per l’articolo molto interessante per infinite applicazioni.
Nella mia vita ingegneristica ho applicato la FFT ai segnali biomedici, alla sintesi musicale (additiva, sottrattiva…) ed al GNSS(Global Navigation Satellite System). Mi permetto di suggerire a tutti coloro che vogliono approfondire il tema della FFT il capitolo 12 del sacro testo ‘The Scientist and Engineer’s Guide to Digital Signal Processing’… si trova anche su internet ed ha delle graficizzazioni che semplificano molto l’apprendimento dell’abbattimento della complessità algoritmica. faccio una provocazione… a chi va di spendere un poco di tempo intelligentemente propongo di implementare una FFT con parallelismo 8 bit per Arduino.
Non sei il primo che fa questa proposta…
Era già successo che qualcuno balenasse questa opportunità.
Dal canto nostro, se volete cimentarvi in questa applicazione, avremo sicuramente spazio da riservarvi.
Ne verrebbe fuori un gran bell’approfondimento. 🙂
Fare una panoramica così veloce della fft non è semplice e ne è venuto fuori un bell’articolo.
Sto seguendo un corso di complementi di misure elettriche e la fft è all’ordine del giorno e le spegazioni son molto ampie del mio prof.
Mi sembra di ricordare però che la potenza complessa S deva essere eseguita con il complesso coniugato della corrente. Sta sera al ritorno verificherò
Grazie per l’articolo
Si, confermo. S può essere espresso come prodotto di U per il coniugato di I come giustamente scritto nella prima formula con I con il puntino sopra, il dubbio mi è venuto quando ho visto la sommatoria nelle righe successive dove mi sembra non sia espressa in questa maniera. O forse è proprio l’espressione in forma di Fourier?
Assolutamente.
Hai ragione. Il prodotto viene fatto per il complesso coniugato del valore della corrente, come da manuale delle operazioni tra fasori 🙂
In effetti mi rendo conto soltanto adesso che il puntino sulla I, uno dei possibili metodi per indicare il complesso coniugato di un numero, si vede poco.
Ottima segnalazione.
Quella è l’espressione in serie di Fourier.
La parte reale e quella che si ritrova come argomento del coseno mentre quella immaginaria è preceduta da “j” ed è quella che ha a che fare con i termini seno.
Quindi prima abbiamo espresso tutto in funzione vettoriale e quindi in termini di fasori e poi abbiamo esplicitato lo sviluppo in sede di Fourier dell’intera espressione.
Naturalmente poi, volta per volta, calcolo per calcolo, andrà visto se quei termini sono uguali o diversi da zero. 🙂
PS: ti ringrazio per i complimenti. Sono davvero felice che l’articolo sia piaciuto e mi auguro che sia risultato chiaro.