
La sicurezza dei dati trasmessi rende il nostro sistema affidabile, ma come possiamo realizzare un sistema del genere? da un punto di vista software, la risposta a questo quesito si trova in un algoritmo di crc.
Gli algoritmi utilizzati per calcolare il checksum sono basati sulla tecnica di CRC. Per usare la terminologia anglosassone, il Cyclic Redundancy Check (CRC) è una tecnica utilizzata per rilevare errori in un flusso di dati trasmessi o in un buffer in memoria. I codici CRC-16 e CRC-CCITT hanno le seguenti caratteristiche:
➤ Rilevano tutti gli errori singoli e doppi
➤ Rilevano tutti gli errori di un numero dispari di bit
➤ Tutti gli errori a raffica di lunghezza massima 16
➤ Il 99,997% degli errori a raffica di lunghezza 17
➤ Il 99,998% degli errori a raffica di lunghezza 18 o più
La richiesta di scambi dati utilizzando sempre più i mezzi di comunicazioni basati su Internet crea l’esigenza di mettere a punto sistemi che assicurano all’utente l’integrità dei dati inviati e ricevuti. A questo punto è opportuno porre l’accento sugli aspetti teorici di questa tecnologia.
Un pò di teoria
L’idea di base del controllo ciclico ridondante è di fare la cosiddetta firma di un blocco di dati. Infatti, questo consiste di un calcolo matematico su un blocco di dati, il risultato che si ottiene è un numero caratteristico che ne rappresenta il contenuto in maniera univoca. L’obiettivo è di ottenere un valore numerico in grado di identificare questo blocco, il valore numerico è anche chiamato checkum (valore di controllo). Il CRC è determinato eseguendo una divisione a modulo 2 per mezzo di un generatore polinomiale, registrando il resto dopo ogni divisione. I polinomi più utilizzati sono:
CRC-16 = X16 + X15 + X2+ 1
CRC-CCITT = X16 + X12 + X5+ 1
CRC-32 = X 32 + X 26 + X 23 + X 22 + X 16 + X 12 +
+ X 11 + X 10 + X 8 + X 7 + X 5 + X 4 + X 2 + X + 1
CRC-8 = X8+ X2 + X + 1
Il CRC-32 è un polinomio standard a 32 bit utilizzato in molte applicazioni (tra cui IEEE 802). Questo calcolo è facilmente ricavato a livello hardware, poiché sfrutta il concetto di registro. Per dimensione dei blocchi di memoria relativamente piccoli, l’algoritmo ne controlla l’integrità. Purtroppo con l’aumentare della sua dimensione, aumenta anche l’inefficienza anche se in maniera trascurabile. Come si è scritto l’aritmetica dei polinomi a coefficienti binari si gestisce con le regole della aritmetica modulo 2, questo implica che:
➤ le somme e le sottrazioni non prevedono riporti; sono pertanto coincidenti ed equivalenti all’OR esclusivo
➤ le divisioni, poi, sono eseguite normalmente. In questa maniera, il divisore “sta” nel dividendo quando il dividendo ha grado maggiore o uguale al divisore, mentre non si può dividere quando il dividendo ha grado inferiore al divisore:
La figura 1 mostra un esempio.
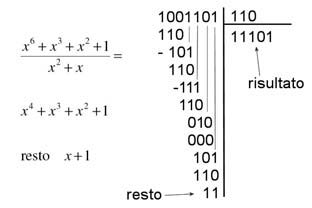
Figura 1: esempio modulo 2
Insieme alla tecnica di rilevazione degli errori, esiste anche la possibilità di, oltre a rilevare un errore, correggere il flusso dei dati. Il codice a rilevazione di errore ha lo scopo di permettere al ricevente di determinare se vi sono stati errori in trasmissione, quindi il codice non ha la finalità di correggere l’errore, ma solo di rilevare che c’è stato. Per raggiungere lo scopo si utilizzano bit di controllo in aggiunta ai bit dei dati e la tecnica utilizzata è di assegnare in trasmissione ai bit di controllo un valore opportuno in funzione dei bit dei dati; in ricezione si calcolano nuovamente i valori dei bit di controllo e si fa la verifica con quelli ricevuti. Per questa ragione si utilizza il codice Hamming. Gli altri codici utilizzati previsti in questa famiglia sono quelli di convoluzione e somma di blocco.
La codifica polinomiale
La tecnica consiste nel considerare i dati (m bit) da inviare come un polinomio di grado m-1. Il trasmettitore e il ricevitore devono accordarsi, cioè il trasmettitore e ricevitore devono utilizzare un polinomio generatore G(x) di grado r. In questo modo, il trasmettitore aggiunge in coda al messaggio una sequenza di bit di controllo (CRC) in modo che il polinomio associato ai bit del frame trasmesso, costituito dall’insieme di dati e CRC, sia divisibile per G(x). Il ricevitore divide il polinomio associato ai dati ricevuti per G(X). Se la divisione ha resto nullo, si assume che la trasmissione sia avvenuta senza errori, mentre se la divisione ha resto non nullo, sono certamente avvenuti degli errori.
Algoritmo
La generazione del codice CRC avviene nel seguente modo:
1) sia M(x) il polinomio associato ai m bit di dati;
2) sia G(x) il polinomio generatore di grado r;
3) si aggiungono r bit a valore 0 in fondo ai bit di dati; il polinomio associato all’insieme di m+r bit è quindi M(x);
4) Si calcola il resto della divisione M(x)/G(x), che sarà un polinomio R(x) di grado inferiore ad r, quindi rappresentativo di una sequenza di r bit;
5) Si costruisce la sequenza di bit associata al polinomio T(x) = M(x)-R(x), che equivale ad aggiungere i bit corrispondenti a R(x) in coda ai dati da inviare: vanno riportati tutti gli r bit associati ad R(x), quindi anche eventuali zeri in testa al resto; questa è una sequenza di m+r bit
A questo punto il polinomio T(x) risulterà divisibile per G(x) con resto nullo. La figura 2 mostra un esempio.

Figura 2: esempio CRC
Il resto della divisione è di 01110, il quoziente 1101010110 e il messaggio che sarà trasmesso sarà uguale al messaggio stesso 1010001101 seguito dal resto, quindi 101000110101110. Il polinomio utilizzato per il calcolo è 110101.
Metodi di calcolo
Per utilizzare l’algoritmo di CRC sono utilizzati due metodi: uno tabellare, nel senso che sono già pre-caricati in un array i valori del CRC o, in alternativa, il calcolo viene fatto a run-time mediante un opportuno algoritmo.
Metodo bitwise
Il calcolo di un CRC è definito bitwise, sel senso che per ricavare un CRC è necessario utilizzare le prerogative di bitwise (cioè gli operatori sui singoli bit). Infatti, gli operatori di bitwise in C sono:
“&“ AND “|” OR
“^” XOR
“~” Complemento a 1 (0=>1, 1=>0) “<<” shift a sinistra
“>>” shift a destra
Gli operatori di shift eseguono un appropriato shift dall’operatore indicato a destra a quello indicato a sinistra. L’operatore destro deve essere positivo. I bits liberati vengono riempiti con zero (cioè non si tratta di una rotazione, con recupero sul lato opposto dei bit shiftati). In questo modo, uno shift a sinistra è equivalente ad una moltiplicazione per 2, mentre uno shift a destra equivale ad una divisione per 2. L’operazione di shift è molto più veloce della reale moltiplicazione o divisione (/); così, se occorrono veloci moltiplicazioni o divisioni per 2 si può utilizzare lo shift. Tipicamente, di seguito c’è un piccolo esempio sull’uso di questi operatori. L’esempio che riportiamo è una funzione (bitcount) che somma 2 bit settati ad 1 un un numero ad 8 bit (unsigned char) passato come argomento alla funzione:
int bitcount(unsigned char x)
{int count;
for (count=0; x!=0; x>>=1);
if (x&01)
count++;
return count;
}
Questa funzione mostra alcuni punti del programma C: il loop “for” non viene usato per semplici operazioni di somma x>>=1 => x=x>>1, il loop “for” shifta ripetutamente a destra x, finché x diventa 0, il controllo “if” utilizza la valutazione dell’espressione x &01. Questa controlla il primo bit di x, ed esegue count++ se questo è 1.
Metodo tabellare
I microprocessori tendono a molto essere migliore ad operare su bytes e words piuttosto che su bits. Il vantaggio di un metodo di questo tipo è che i valori di CRC possono essere pre-calcolati e messi in una tabella (un array in C). Nel processore MSP430 le tabelle presenti in memoria possono essere messi in memorie flash con la possibilità di accedere a run-time o a link-time. La dimensione preferibile per tabelle di questo genere sono tipicamente di 256 parole, per trovare un giusto compromesso tra memoria e CPU. Più grande è la tabella di riferimento e più si riduce il tempo di run-time, in questo modo, però, è possibile trovare un accordo tra la dimensione della tabella e (con i suoi impatti in memoria) con i tempi attesi. Gli algoritmi di questo tipo richiedono di solito molta memoria e la velocità di computazione può anche risultare marginale, così come lo è su MPS430.
Ambiente di test e verifica dell’algoritmo
I progetti, sia per Visual C++ che per IAR, include un singolo programma principale per il testing e la verifica dell’algoritmo di CRC. La parte assembly sono inclusi solo se, al momento della costruzione del nostro eseguibile, viene utilizzato il simbolo __ICC430__. Questo simbolo è automaticamente definito se utilizziamo la versione per Embedded Workbench. Il messaggio di test utilizzato per verificare l’algoritmo di CRC è la sequenza di caratteri >ASCII 123456789. Occorre tenere presente che questa sequenza on è una stringa, cioè la sequenza non termina con il carattere di terminazione \0. AL termine dl calcolo del CRC, il valore viene visualizzato sul terminale di uscita attraverso la funzione di I/O printf(). L’utente può così verificare il risultato atteso. Il listato 1 mostra una possibile implementazione di un CRC liberamente disponibile dalla distribuzione cygwin.
/* Compute checksum Author: Johan W. Stevenson */
/* Copyright 1988 by Johan W. Stevenson */
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
int errs;
#if __STDC__
int main(int argc, char **argv);
void crc(char *fname);
#else
void crc();
#endif
int main(argc, argv)
int argc;
char **argv;
{
char line[256];
if (argc <= 1)
crc((char *) 0);
else if (argc == 2 && strcmp(argv[1], “-“) == 0)
while (fgets(line, sizeof line, stdin) != NULL) {
if (line[strlen(line) - 1] == ‘\n’)
line[strlen(line) - 1] = ‘\0’;
crc(line);
}
else
do {
crc(argv[1]);
argv++;
argc—;
} while (argc > 1);
return(errs != 0);
}
static unsigned short crctab[256] = {
0x0000, 0x1021, 0x2042, 0x3063, 0x4084, 0x50a5, 0x60c6,
0x70e7, 0x8108, 0x9129, 0xa14a, 0xb16b, 0xc18c, 0xd1ad,
0xe1ce, 0xf1ef, 0x1231, 0x0210, 0x3273, 0x2252, 0x52b5,
0x4294, 0x72f7, 0x62d6, 0x9339, 0x8318, 0xb37b, 0xa35a,
0xd3bd, 0xc39c, 0xf3ff, 0xe3de, 0x2462, 0x3443, 0x0420,
0x1401, 0x64e6, 0x74c7, 0x44a4, 0x5485, 0xa56a, 0xb54b,
0x8528, 0x9509, 0xe5ee, 0xf5cf, 0xc5ac,0xd58d, 0x3653,
0x2672, 0x1611, 0x0630, 0x76d7, 0x66f6, 0x5695, 0x46b4,
0xb75b, 0xa77a, 0x9719, 0x8738, 0xf7df, 0xe7fe, 0xd79d,
0xc7bc, 0x48c4, 0x58e5, 0x6886, 0x78a7, 0x0840, 0x1861,
0x2802, 0x3823, 0xc9cc, 0xd9ed, 0xe98e, 0xf9af, 0x8948,
0x9969, 0xa90a, 0xb92b, 0x5af5, 0x4ad4, 0x7ab7, 0x6a96,
0x1a71, 0x0a50, 0x3a33, 0x2a12, 0xdbfd, 0xcbdc, 0xfbbf,
0xeb9e, 0x9b79, 0x8b58, 0xbb3b, 0xab1a, 0x6ca6, 0x7c87,
0x4ce4, 0x5cc5, 0x2c22, 0x3c03, 0x0c60, 0x1c41, 0xedae,
0xfd8f, 0xcdec, 0xddcd, 0xad2a, 0xbd0b, 0x8d68, 0x9d49,
0x7e97, 0x6eb6, 0x5ed5, 0x4ef4, 0x3e13, 0x2e32, 0x1e51,
0x0e70, 0xff9f, 0xefbe, 0xdfdd, 0xcffc, 0xbf1b, 0xaf3a,
0x9f59, 0x8f78, 0x9188, 0x81a9, 0xb1ca, 0xa1eb, 0xd10c,
0xc12d, 0xf14e, 0xe16f, 0x1080, 0x00a1, 0x30c2, 0x20e3,
0x5004, 0x4025, 0x7046, 0x6067, 0x83b9, 0x9398, 0xa3fb,
0xb3da, 0xc33d, 0xd31c, 0xe37f, 0xf35e, 0x02b1, 0x1290,
0x22f3, 0x32d2, 0x4235, 0x5214, 0x6277, 0x7256, 0xb5ea,
0xa5cb, 0x95a8, 0x8589, 0xf56e, 0xe54f, 0xd52c, 0xc50d,
0x34e2, 0x24c3, 0x14a0, 0x0481, 0x7466, 0x6447, 0x5424,
0x4405, 0xa7db, 0xb7fa, 0x8799, 0x97b8, 0xe75f, 0xf77e,
0xc71d, 0xd73c, 0x26d3, 0x36f2, 0x0691, 0x16b0, 0x6657,
0x7676, 0x4615, 0x5634, 0xd94c, 0xc96d, 0xf90e, 0xe92f,
0x99c8, 0x89e9, 0xb98a, 0xa9ab, 0x5844, 0x4865, 0x7806,
0x6827, 0x18c0, 0x08e1, 0x3882, 0x28a3, 0xcb7d, 0xdb5c,
0xeb3f, 0xfb1e, 0x8bf9, 0x9bd8, 0xabbb, 0xbb9a, 0x4a75,
0x5a54, 0x6a37, 0x7a16, 0x0af1, 0x1ad0, 0x2ab3, 0x3a92,
0xfd2e, 0xed0f, 0xdd6c, 0xcd4d, 0xbdaa, 0xad8b, 0x9de8,
0x8dc9, 0x7c26, 0x6c07, 0x5c64, 0x4c45, 0x3ca2, 0x2c83,
0x1ce0, 0x0cc1, 0xef1f, 0xff3e, 0xcf5d, 0xdf7c, 0xaf9b,
0xbfba, 0x8fd9, 0x9ff8, 0x6e17, 0x7e36, 0x4e55, 0x5e74,
0x2e93, 0x3eb2, 0x0ed1, 0x1ef0
};
/* Updcrc macro derived from article Copyright (C) 1986
Stephen Satchell.
* NOTE: First argument must be in range 0 to 255.
* Second argument is referenced twice.
*
* Programmers may incorporate any or all code into their programs,
giving proper credit within the source. Publication of
the source routines is permitted so long as proper credit is
given to Stephen Satchell, Satchell Evaluations and Chuck
Forsberg, Omen Technology.
*/
#define updcrc(cp, crc)(crctab[((crc>>8)& 255)]^(crc <<8)^cp)
void crc(fname)
char *fname;
{
register int c;
register long len = 0;
register unsigned short crc = 0;
register FILE *fp;
if (fname == NULL)
fp = stdin;
else if ((fp = fopen(fname, “r”)) == NULL) {
fprintf(stderr, “crc: cannot open %s\n”, fname);
errs++;
return;
}
while ((c = getc(fp)) != EOF) {
len++;
crc = updcrc(c, crc);
}
/* printf(“%05u %6ld”, crc, len); */
printf(“%x”,crc);
if (fname) {
printf(“ %s”, fname);
fclose(fp);
}
printf(“\n”);
}
| Listato 1 - Calcolo di CRC |




