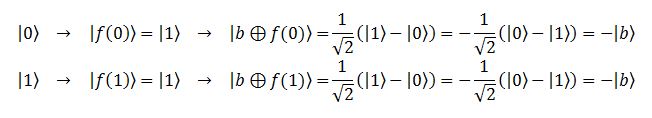Dentro un computer quantistico: l’algoritmo di Deutsch-Jozsa

La filosofia di vita dell’algoritmista si può riassumere in cinque parole: Si può fare di meglio? Perché, in effetti, i motivi che spingono allo sviluppo di un nuovo algoritmo sono due: risolvere un problema che non è ancora stato risolto, o risolvere meglio un problema che è già stato risolto. Le prestazioni, al tempo dei Big Data, sono tutto. E il potenziale incremento di prestazioni rappresenta anche una delle forze che trainano lo sviluppo degli algoritmi per computer quantistici. Oggi, ve ne presenteremo uno, non particolarmente utile nel mondo reale ma che evidenzia benissimo quanto meglio si possa fare con un computer quantistico. E, ovviamente, una certa dose d’ingegno.

PARLA L’ORACOLO

Oltre ad Alice e Bob (e magari qualche loro amico o nemico, tipo Eve o Charlie), uno dei principali frequentatori di questo reame è l’Oracolo. L’Oracolo è una scatola nera. Gli fai una domanda, ti da una risposta. Non hai idea del come generi questa risposta. Alla meglio, puoi avere delle informazioni su qualche sua caratteristica.

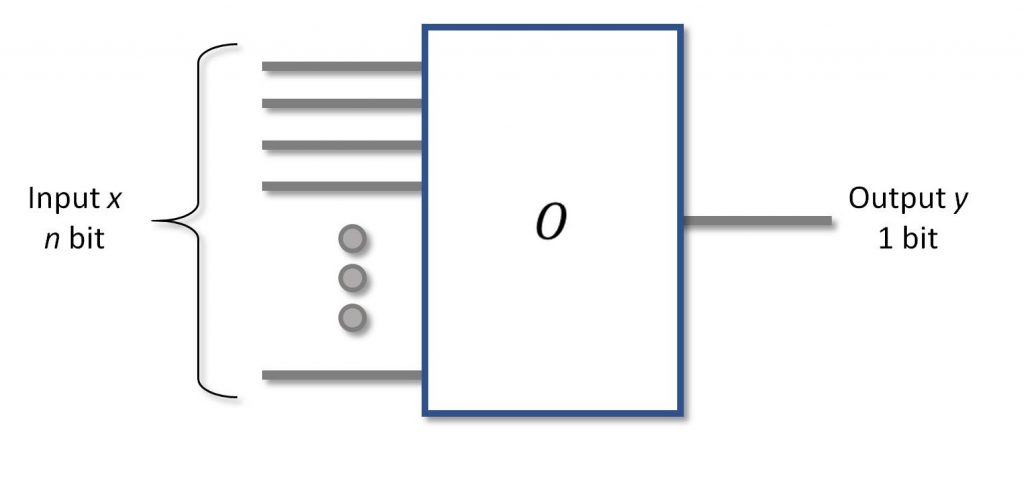
Figura 1: Un Oracolo

Nel caso dell’algoritmo di Deutsch-Jozsa, ci viene dato di sapere che l’Oracolo lavora in logica binaria. Dunque, presa una serie di bit in ingresso, ne restituisce un altro in uscita. Una comune funzione binaria. L’unica cosa in più che sappiamo è che questa funzione è o costante, o bilanciata, non ci sono alternative. “Costante” significa che è costante, che restituisce sempre lo stesso risultato indipendentemente dall’ingresso. “Bilanciata” significa che per metà degli ingressi restituisce un valore e per l’altra metà l’altro. Lo scopo dell’algoritmo è determinare, nel modo più rapido possibile, di che Oracolo si tratta. Sì, non è un algoritmo concepito per rivoluzionare il mondo. Dunque, supponendo di non sapere nulla di meccanica quantistica, come possiamo risolvere questo problema? Necessariamente, interrogando un certo numero di volte (il minore possibile) l’Oracolo e cercando di capire, dalle sue risposte, di che Oracolo si tratta. Un approccio un pò poliziesco, se volete, ma è l’unico disponibile.

Ora, quante volte dobbiamo interrogare l’Oracolo? Come dice sempre l’ingegnere saggio, dipende. In questo caso, da quanto siamo fortunati. Nel caso migliore, bastano due interrogazioni. Se, ad esempio, l’Oracolo ci rispondesse zero la prima volta e uno la seconda, sicuramente la funzione che implementa non può essere costante, e dunque deve essere bilanciata, non essendoci altre alternative. Nel caso peggiore, ci può volere la metà più uno dei tentativi possibili. Se ci riflettete un attimo, se siamo veramente sfortunati, l’Oracolo potrebbe risponderci sempre con lo stesso valore, diciamo uno. Dopo metà delle interrogazioni possibili, se la funzione è costante, risponderà uno anche al tentativo successivo, ma se è bilanciata al tentativo successivo dovrà rispondere necessariamente zero. Ricordate, infatti, che una funzione bilanciata dà metà delle volte uno e l’altra metà zero, e gli uno li abbiamo finiti con la prima metà dei tentativi possibili - dunque, al tentativo successivo saremo sicuramente in grado di distinguere i due casi. Volendo dare due numeri, supponiamo che l’ingresso dell’Oracolo sia a 10 bit. Se siamo fortunati, scopriremo di che Oracolo si tratta al secondo tentativo, se siamo sfortunati, di tentativi ce ne serviranno:

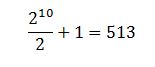
che è un pò di più di due. Se di bit ce ne fossero 20 (non tanto, alla fine), i tentativi del caso peggiore salgono a:

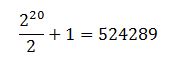
che con 30 bit diventano:

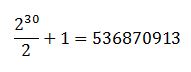
E via di questo passo. Il numero di tentativi cresce rapidamente con il numero di bit n dell’ingresso. In particolare, cresce in maniera esponenziale con la larghezza dell’ingresso. Comportamenti di questo tipo per grandi valori di n (si chiamano asintotici, in memoria di ciò che accade ad Analisi I, quando si va verso l’infinito) sono il male più assoluto per chi progetta algoritmi, perché dimostrano che l’algoritmo che hanno progettato (in questo caso, la banale interrogazione ripetuta dell’Oracolo) diventa straordinariamente lento già per ingressi di dimensione modesta (che saranno mai, al giorno d’oggi, 30 bit). Andamenti asintotici esponenziali rientrano nella categoria dei problemi intrattabili; algoritmi molto efficienti avranno andamenti lineari con l’ingresso (nel senso che con un ingresso a 30 bit bastano una trentina di tentativi per avere la soluzione), ma ci si accontenta felicemente anche di andamenti semilogaritmici. Già comportamenti quadratici con l’ingresso (con 30 bit servono 900 tentativi) fanno storcere il naso, ma restano comunque migliori dell’esponenziale. L’algoritmista, di fronte ad una cosa del genere, ha solo due possibilità. La prima è procurarsi un hardware migliore: un supercomputer, una batteria di GPU, quello che vi pare. Ma questa è la strada semplice, quella che non richiede di bruciare nemmeno un neurone e quella che, magari, per 40 bit richiede comunque un’enormità di tempo. La seconda è chiedersi: Si può fare meglio?

SI PUO' FARE DI MEGLIO?

Diciamo che, per tentare di fare di meglio, vogliamo sfruttare l’incredibile (dicono) potenza dei computer quantistici. Per fare questo, però, dobbiamo prima fare in modo che l’Oracolo si adatti a questo radicale cambio di hardware, perché la sua implementazione come in Figura 1 non va d’accordo con questo paradigma. Se quello della Figura 1 è a tutti gli effetti un circuito, non è però un circuito quantistico: se ricordate, infatti, i circuiti quantistici sono tutti reversibili, nel senso che, se usassimo le uscite del primo come ingresso ad un secondo uguale, all’uscita del secondo dovremmo riavere l’ingresso del primo.

Figura 2: L'Oracolo non è invertibile

In pratica, dovrebbe accadere qualcosa come ciò che accade nella Figura 2, ed è ovvio che qui non succede, se non altro perché l’ingresso del secondo Oracolo è a n bit mentre l’uscita del primo è a un bit soltanto. Se ricordate ciò che abbiamo detto quando abbiamo introdotto i circuiti quantistici, questi tipicamente hanno, proprio per questo motivo, tanti ingressi quante uscite.

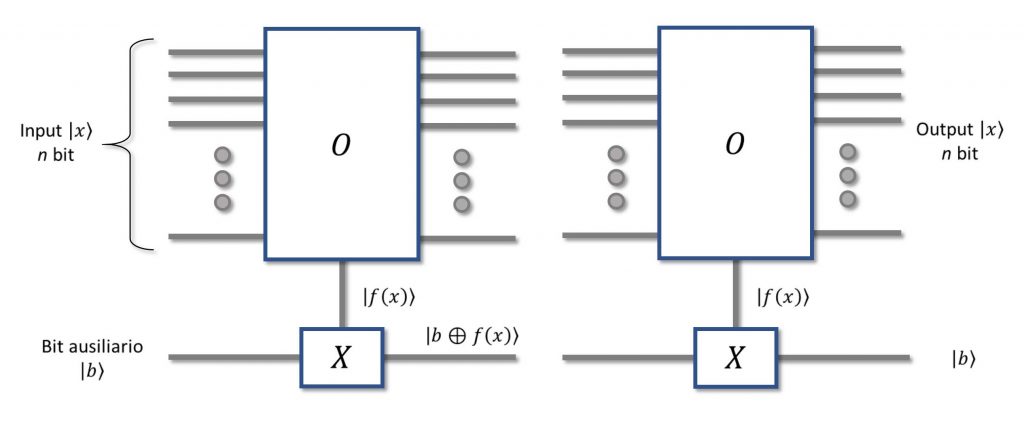
Figura 3: Un Oracolo invertibile

La modifica da fare per rendere invertibile, per quanto possa sembrare non ovvia, è mostrata nella Figura 3. Abbiamo aggiunto un pò di linee, e adesso l’ingresso viene replicato in uscita, pronto ad essere riusato per il circuito successivo. In più, abbiamo aggiunto un bit ausiliario perché comunque, oltre a replicare l’ingresso, dobbiamo dare anche fuori la risposta dell’Oracolo. Notare dalla figura, però, come questa linea in più non contenga direttamente la risposta, ma lo XOR con il bit ausiliario in ingresso. Il motivo è duplice. Innanzitutto, c’è sempre la reversibilità. Vogliamo riavere, sul bit ausiliario in uscita dal secondo Oracolo, il bit ausiliario b che abbiamo dato in ingresso al primo. Ora, se il secondo Oracolo si vede in ingresso lo XOR tra b e la risposta del primo, sulla sua uscita avremo:

in quanto lo XOR di un bit con sè stesso restituisce sempre 0. Il secondo motivo, come vedremo tra un attimo, è che questo XOR è il punto cruciale per la soluzione del problema.

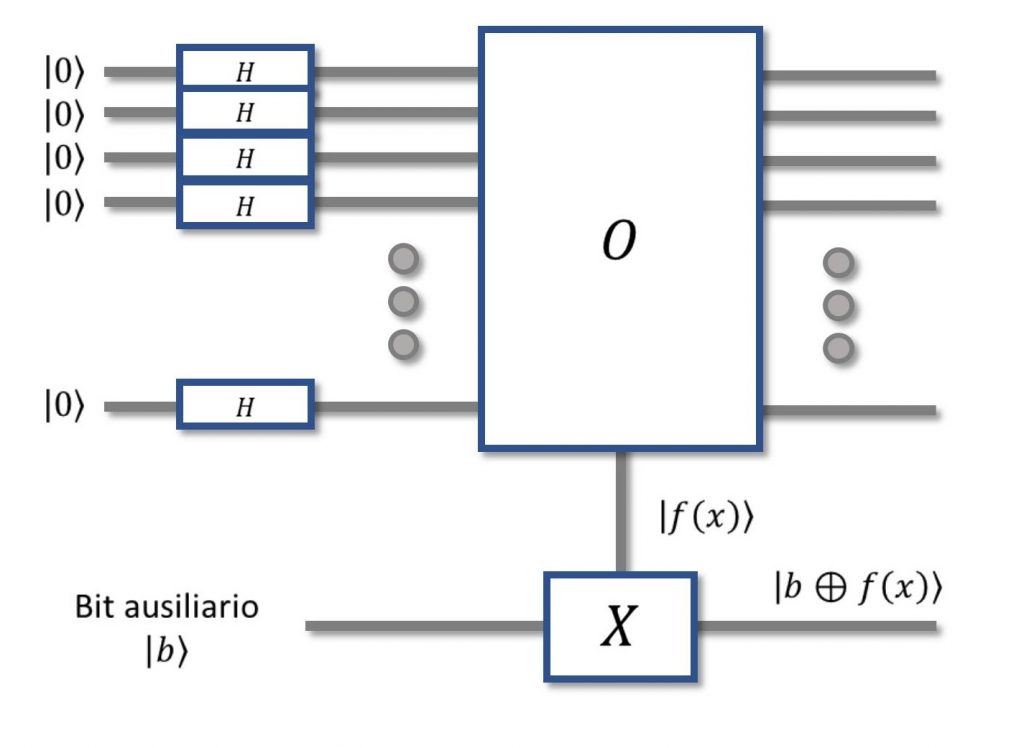
Figura 4: Hackerare l'Oracolo

Adesso viene il bello. Come facciamo a battere quest’Oracolo? Considerato che abbiamo deciso di lavorare con i computer quantistici, la prima idea che potrebbe venirci in mente è quella di mettere tutti i bit in ingresso a zero e farli passare attraverso altrettante porte di Hadamard, come nella Figura 4. Come ormai dovremmo aver imparato, le porte di Hadamard prendono i qubit in ingresso e li trasformano in un’equa sovrapposizione di tutte le combinazioni possibili di qubit. Ad esempio, nel caso a due bit:

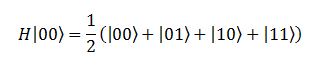
Dunque, favorire quest’ingresso all’Oracolo significa che lo facciamo lavorare contemporaneamente su tutte le possibili combinazioni di qubit in ingresso. In pratica, è come se gli stessimo facendo tutte le domande possibili tutte insieme. E, se l’Oracolo è quantistico, ci fornirà tutte le risposte contemporaneamente, codificandole in una qualche particolare sovrapposizione dello stato in uscita. Forse, possiamo cominciare a intuire come l’approccio quantistico potrebbe velocizzare l’algoritmo. Se disponiamo in un colpo solo di tutte le risposte, forse analizzandole adeguatamente potremmo riuscire a capire di che Oracolo si tratta. “Analizzare” qui si traduce ovviamente in “misurare”, e questo significa che il nostro scopo è riuscire a capire di che Oracolo si tratta con il minor numero possibile di misure.

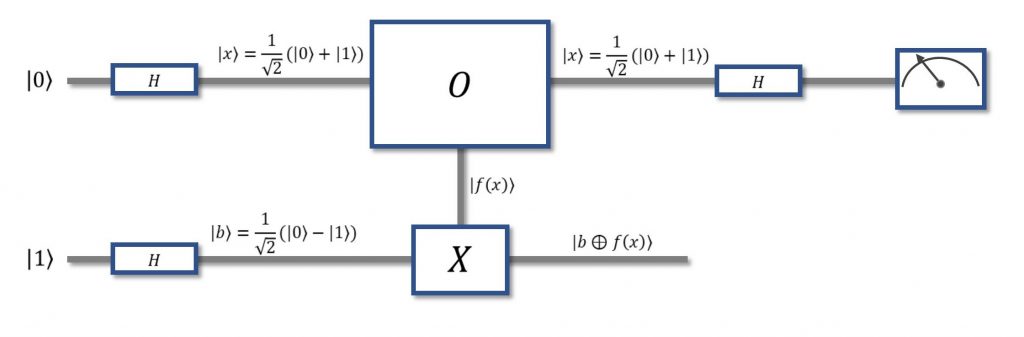
Figura 5: Un Oracolo a un bit

Come spesso si fa quando si cerca di sviluppare un algoritmo, partiamo da un caso semplice, quello di Oracolo a un bit mostrato nella Figura 5. Qualcosa di molto interessante accade se il bit ausiliario in fondo, anziché essere generico, lo mettiamo a uno, e facciamo passare anche lui per una porta di Hadamard. Supponiamo che l’Oracolo sia costante. Dunque, emetterà o sempre zero o sempre uno, per entrambi i casi che gli si possono presentare in ingresso. Diciamo che emette sempre zero. Questo zero viene usato per controllare la XOR che, ve lo ricordiamo, altro non è che una CNOT, ossia una porta che inverte il bit controllato se e solo se il bit di controllo è a uno. Ora, l’input dell’Oracolo è:

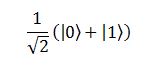
che, come dicevamo, equivale a dire che applichiamo entrambi i casi possibili per un ingresso a un bit (0 e 1) contemporaneamente. L’Oracolo lavora su di essi indipendentemente e restituisce:

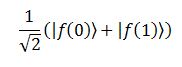
che altro non è che la somma dei due risultati. Conviene quindi, per comodità, considerare i due casi separatamente, come faremmo per un Oracolo classico, e poi ricombinarli in seguito. Basta che ci ricordiamo che l’elaborazione, in realtà, avviene in parallelo. Per i due casi in ingresso abbiamo quindi:

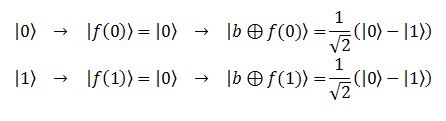
dove nell’ultima colonna abbiamo riportato l’effetto sul bit ausiliario: essendo la risposta dell’Oracolo sempre nulla, la CNOT non lavora e tutto resta immutato. Leggermente più interessante è il caso in cui l’Oracolo restituisca sempre 1. Qui abbiamo:

[...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2469 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.