Il progressivo innalzarsi delle frequenze di lavoro in elettronica digitale rende opportuna l’importazione di tecniche proprie della radiofrequenza o microonde, ad esempio i Parametri S per la descrizione delle proprietà delle interconnessioni, e più in generale, di reti passive.
La maggior parte di noi ha studiato Elettronica e le leggi dei circuiti seguendo il metodo “classico”, ovvero partendo dallo studio di semplici circuiti in corrente continua, esaminando poi i fenomeni magnetici, semplici circuiti in corrente alternata sinusoidale e cosi via.
In realtà sappiamo dalla fisica che le leggi dei circuiti introdotte in tale modo sono una serie di approssimazioni, molto utili ma valide solo quando precise condizioni siano soddisfatte. In particolare, sono valide quando le dimensioni fisiche degli oggetti studiati siano molto più piccole della lunghezza d’onda dei segnali elettrici coinvolti. Un buon criterio consiste nel lavorare con oggetti di dimensioni inferiori ad un decimo (meglio ancora un ventesimo) della lunghezza d’onda della componente di frequenza più elevata in gioco. Consideriamo ad esempio la frequenza di distribuzione dell’energia elettrica alternata a 50 Hz. La corrispondente lunghezza d’onda è di ben 6000 km in aria (lunghezza d’onda uguale alla velocità della luce diviso la frequenza). Tutti i circuiti che troviamo nelle nostre case possono quindi essere tranquillamente studiati con le classiche leggi di Ohm, eccetera, senza che vi sia modo di rendersi conto di errori o approssimazioni. Notare che anche lavorando a 50 Hz, le cose cambiano se consideriamo le linee di trasmissione dell’energia elettrica che, ad esempio nel caso di dorsali di distribuzione, si possono avvicinare a lunghezze critiche. I fenomeni elettrici trovano una descrizione esaustiva ed elegante quando trattati secondo la loro reale natura di campi ed onde. Purtroppo, tali descrizioni sono matematicamente complesse e di difficile applicazione pratica. Il curriculum di studi classici trova una valida giustificazione nella validità delle tecniche ottenute per la maggior parte dei casi pratici ed anche nella grande semplificazione concettuale e matematica che rende possibile nell’insegnamento dell’elettromanetismo. Questo però non deve farci mai dimenticare la reale natura dei fenomeni elettrici nel loro complesso e la loro intrinseca caratteristica ondulatoria. L’aumentare delle frequenze operative e la costante riduzione dei tempi di transizione tra stati dei segnali logici (rise e fall time), fanno si che frequenze sempre più elevate e quindi, lunghezze d’onda sempre più corte, siano presenti nei circuiti su cui tecnici che si occupano di apparecchiature digitali si trovano ad operare. Le ipotesi di fondo non reggono più e man mano che le frequenze crescono, il comportamento dei segnali elettrici in termini di onde, più o meno guidate, propagate in mezzi fisici assume un peso sempre maggiore ed evidente. Contemporaneamente, concetti come tensione, e corrente perdono la loro utilità nella descrizione dei fenomeni elettrici, ed in qualche caso anche il loro significato fisico. Al crescere delle frequenze, misurare tensioni e correnti diviene progressivamente più difficoltoso, mentre diventa sempre più conveniente, sebbene non semplice, misurare parametri tipici della propagazione ondosa, quali onde riflesse e trasmesse. L’insieme di queste ragioni portano alla necessità di affiancare ai familiari concetti di tensione e corrente, nuovi parametri con cui descrivere le proprietà dei circuiti e dei loro componenti in un ampio spettro di frequenza. Per l’ingegnere digitale, questo è di particolare interesse per la descrizione delle reti passive costituenti le interconnessioni di segnale ed alimentazione di circuiteria digitale veloce. Si pensi ad esempio a link seriali funzionanti a molti Gbit, oramai comuni nei nostri PC oppure alla distribuzione di alimentazione di una scheda contenete integrati veloci. Diventa importante analizzare e misurare la “trasparenza” di ogni elemento del canale di comunicazione, tracce su pcb, connettori, cavi. I Parametri-S o Parametri di Diffusione (Scattering in inglese, da cui la S per brevità) servono appunto a questo scopo, tolti di peso dal mondo dell’ingegneria delle microonde e radiofrequenza dove sono nati ed hanno proficuamente lavorato fino ad oggi. Una ulteriore complicazione per l’ingegnere digitale, è costituita dalla crescente convenienza a lavorare anche, se non prevalentemente, nel dominio della frequenza. Il familiare grafico “da oscilloscopio”, con il tempo sulle ascisse non rende infatti evidente cosa succede alle alte frequenze, pur avendo spesso tutta l’informazione comunque racchiusa in se.
DEFINIZIONE E SIMBOLISMO
Non fatevi scoraggiare vedendo formule e logaritmi, la matematica richiesta è in realtà poca per i nostri scopi. In estrema sintesi, i Parametri di Diffusione descrivono come un segnale incidente viene trasmesso e riflesso da ogni interconnessione di una rete elettrica, rendono quindi conto del comportamento “ondoso” dei segnali elettrici, invece che basarsi su relazioni tra tensioni e correnti. Prima di esaminarli da vicino, abbiamo bisogno di introdurre alcuni termini e concetti. In generale, gli ingressi e le uscite di una generica rete circuitale vengono definiti ‘Port’ nel mondo alta frequenza. Ogni Port è composto dal terminale “caldo”, il segnale che ci interessa, ed il proprio segnale di ritorno, impropriamente definito “massa”, consiste quindi in due connessioni fisiche. Il Port è caratterizzato da una impedenza caratteristica ben definita, tipicamente 50 ohm. Esempio tipico di Port è il connettore coassiale. I puristi RF mi perdoneranno, ma potreste in prima approssimazione leggere “connettore” per “port”. Ovviamente, bisogna ricordare che non sempre esiste un connettore fisico in corrispondenza dei port definiti per una rete generica. Risulta spesso conveniente esprimere le misure in deciBel, cioè il logaritmo del rapporto tra la grandezza di interesse ed un valore di riferimento, logaritmo moltiplicato per 20 nel caso di rapporti tra tensioni o correnti, moltiplicato per 10 nel caso di rapporti tra potenze:
V(dB) = 20 log(V2/V1) V(dB) =
= antilog (V(dB)/20)
I(dB) = 20 log(I2/I1) I(dB) =
= antilog (I(dB)/20)
P(dB) = 10 log(P2/P1) P(dB) =
= antilog (P(dB)/10)
Il vantaggio nell’uso di unità di misura logaritmiche dovrebbe essere facilmente catturabile dalla tabella 1.
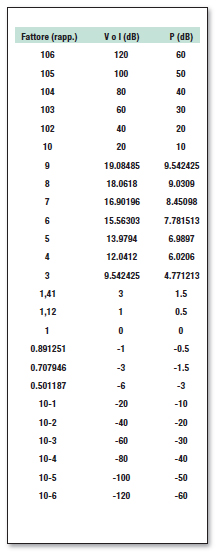
Tabella 1: deciBel.
Attraverso un numero compatto in decibel si possono esprimere valori con una dinamica molto ampia, cioè molto piccoli o molto grandi, senza trascinarsi lunghi numeri con virgole o moltiplica tori. Un altro concetto utile nel seguito, preso direttamente dalla teoria delle linee di trasmissione, è la condizione di massimo trasferimento di potenza. Questo si realizza su linee ad impedenza costante Z, alimentate da una sorgente di impedenza interna pari a Z e chiuse su un carico pure pari a Z. La linea di trasmissione, o rete, ha in tal caso riflessioni nulle e tutta la potenza fornita dal generatore viene consegnata al carico, fluendo lungo una struttura ideale di caratteristiche elettriche e fisiche omogenee. Vediamo ora la definizione dei Parametri-S. Ognuno dei Parametri-S di uno specifico Port è il rapporto tra il segnale incidente ed il segnale riflesso (o trasmesso , quando più di un port sia coinvolto, come vedremo tra poco). Tutti i segnali qui considerati sono onde sinusoidali. Avremo quindi bisogno di due parametri numerici per descriverli completamente: Ampiezza e Fase. In generale, avremo quindi:
S (Ampiezza) = Ampiezza Onda Uscita
/ Ampiezza Onda Ingresso
S (Fase) = Fase Onda Uscita – Fase Onda Ingresso
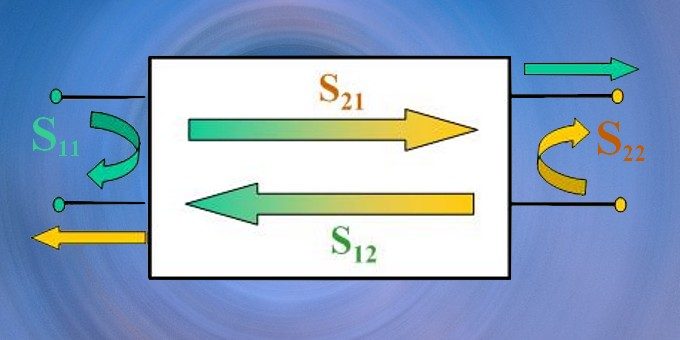
L’ordine di numerazione dei Port è importante per mantenere coerenza nella rappresentazione delle reti. L’ordine raccomandato è evidenziato nella figura 1.

Figura 1: numerazione raccomandata per i
Port di una generica rete.
Tale convenzione è facilmente estensibile ad un numero arbitrario di ingressi/uscite, mantenendo tutti i Port dispari adiacenti tra loro e tutti i Port pari adiacenti tra loro. Il Port dispari N risulta sempre connesso con il Port pari N+1. Ricordiamo che ogni port ha due connessioni fisiche, ciascuno di essi è sostanzialmente considerabile una connessione coassiale. Due indici sono usati per identificare a quale combinazione di Ports il Parametro si riferisca, quindi da ad es. S11, S21. Il primo indice si riferisce al Port di Uscita, il secondo al Port di Ingresso. Skj = Onda uscita Port k / Onda ingresso Port j Tale convenzione, di primo acchito non intuitiva, deriva dal formalismo matematico connesso all’uso dei Parametri S, l’algebra delle matrici, di cui non avremo ulteriormente bisogno in questa sede.
Senza alcun riferimento alla struttura interna della rete sotto analisi, la risposta ad un segnale entrante nel Port 1 ed uscente (riflessa) dal Port 1 verrà definito S11. La risposta ad un segnale entrante nel Port 1 ed uscente dal Port 2 verrà definito S21 e cosi via. Il valore numerico di un parametro S è sempre compreso tra 0 ed 1, per definizione, trattandosi di un rapporto. Come anticipato, il valore è spesso espresso in dB:
SdB = 20 * log (valore di S)
Per ogni frequenza, il singolo parametro S avrà in generale un valore diverso. Il parametro è inoltre un numero complesso, quindi può essere rappresentato come modulo ed angolo o come parte reale più parte immaginaria. L’insieme dei valori può essere presentato su un grafico cartesiano con le frequenze in ascisse, rendendo ben visibile quindi l’andamento del parametro considerato al variare della frequenza. Le reti composte da elementi lineari e passivi (resistenze, condensatori, induttori, cavi…), il caso che ci interessa qui, hanno le seguenti proprietà:
- S11 ed S22 sono in generale diversi tra loro, a meno che la rete non sia simmetrica.
- S12 ed S21 sono sempre uguali.
L’insieme dei Parametri S (matrice se vogliamo un maggior rigore espressivo) descrive in modo preciso il comportamento in frequenza della rete. L’occhio allenato riconosce le proprietà fondamentali della rete dall’andamento dei grafici. Vediamone qualche aspetto applicativo, considerando per semplicità espressiva ancora la rete con due port.
SIGNIFICATO DEI PARAMETRI-S
Per ragioni storiche, il modulo del Parametro S di riflessione, S11, è chiamato “Return loss” ed il modulo del parametro di trasmissione S21 è chiamato “Insertion Loss”. Queste definizioni sono ancora convenienti e di uso comune. Return Loss, rapporto tra onda riflessa e onda incidente dallo stesso port, rappresenta la porzione di segnale riflessa verso la sorgente a causa di discontinuità dell’impedenza della rete sotto esame (ad esempio traccia di un pcb con larghezza variabile). Si può considerare come il coefficiente di riflessione della rete nel dominio della frequenza. Insertion Loss rappresenta la porzione di segnale persa nel trasferimento tra i due Port considerati, a causa di disadattamento di impedenza, effetti di risonanze, accoppiamenti induttivi o capacitivi. I parametri S sono molto laboriosi da calcolare manualmente. In pratica, essi sono generalmente risultato di misura o simulazione circuitale (ad esempio SPICE). Una importante aspetto da tener presente è che, mentre nel dominio del tempo osserviamo i valori istantanei delle tensioni riflesse o trasmesse, la risposta della rete in termini di Parametri S nel dominio della frequenza rappresenta uno stato stabile, la risposta complessiva a transitori esauriti. Ogni corrispondenza con l’intima struttura fisica della rete o interconnessione viene persa nei parametri S, mentre ad esempio nell’analisi di riflessioni nel dominio del tempo (Time Domain Reflection, TDR) è possibile determinare in quale punto fisico della linea di trasmissione si sia generata una riflessione. Uno dei parametri da rispettare nella realizzazione di interfacce seriali veloci è proprio un valore massimo di insertion loss. Saper leggerne il grafico diviene quindi indispensabile.
ANALISI DI INTERCONNESSIONI CON L’USO DEI PARAMETRI S
Una rete “trasparente” al segnale è una struttura particolarmente desiderabile in molte applicazioni. Riconoscerne le caratteristiche nei grafici di parametri S è quindi importante. La trasparenza di una rete si può intendere come misura della qualità dell’interconnessione realizzata per mezzo di essa. Tre caratteristiche definiscono una interconnessione trasparente:
- L’impedenza lungo la linea non manifesta disadattamenti.
- Le perdite sono basse e la maggior parte del segnale è trasmessa.
- Gli accoppiamenti con tracce adiacenti sono trascurabili.
S11 Return Loss di una connessione trasparente (ideale)
S11 = Onda uscita Port 1/Onda ingresso Port 1
Quando l’impedenza della connessione è prossima a quella dei Port, la riflessione verso la sorgente tende a 0 (per il teorema della massima trasmissione di potenza) e Return Loss sarà quindi tendente al valore numerico 0 (numero positivo molto minore di 1) e praticamente rappresentato in dB da un grande valore negativo. Il valore in dB viene limitato ad un numero finito dal rumore di fondo della strumentazione o delle caratteristiche dell’ambiente di simulazione, praticamente si ottengono valori prossimi a - 100dB. Tanto maggiore diventa il disadattamento di impedenza, tanto più Return Loss tende ad assumere valore 1 (0 dB), corrispondente a 100% di riflessione (caso per cui si ha S11 = 1).
S21 INSERTION LOSS DI UNA CONNESSIONE TRASPARENTE (IDEALE)
S21 = Onda uscita Port 2 / Onda ingresso Port 1
Tanto migliore è l’interconnessione (adattata in impedenza e basse perdite), tanto più segnale verrà trasmesso al Port di uscita, tanto più Insertion Loss sarà prossimo al valore 1 (0 dB). Abbiamo S21 = 1 nel caso ideale linea di trasmissione 50 ohm uniforme connessa a Ports 50 ohm. Tanto maggiore è la
porzione di segnale non trasferita, tanto più grande è il modulo di S21 rappresentante la perdita di inserzione.
Notiamo che S21 è rappresentato da un numero negativo, decrescente al crescere della porzione di segnale persa. Parlando di “grande perdita di inserzione” indichiamo quindi un numero negativo di decibel con modulo grande, ad esempio -60dB.
Il modulo di Insertion Loss è una misura dell’energia dispersa che non raggiunge il Port di uscita.
L’energia non trasmessa in uscita può essere dispersa come:
- Emissioni Radiate
- Perdite trasformate in calore nei conduttori e nel dielettrico.
- Trasferimenti verso tracce vicine (Accoppiamenti).
- Riflessioni verso la sorgente
Nella maggior parte dei casi, l’impatto delle Emissioni Radiate su S21 è trascurabile a causa della piccola quantità di energia in gioco.
Le perdite di potenza dovute a risonanze o accoppiamenti sono evidenziate nei grafici dei parametri S come picchi negativi in corrispondenza dei campi di frequenza in cui i fenomeni sono significative. Perdite proporzionali alla frequenza sono invece evidenziate da una curva discendente. Quando le altre cause siano state rimosse come risultato di una accurata progettazione, S21 è una misura diretta dell’attenuazione della linea dovuta alle perdite nel dielettrico e nel conduttore. Misurato in dB, vediamo un valore negativo che aumenta in modulo (diviene più negativo) proporzionalmente alla frequenza. Per semplicità e per meglio familiarizzare con il concetto, possiamo considerare S21 come una sorta di Diagramma di Bode della nostra interconnessione o rete. Noti i Parametri S, è possibile calcolare le familiari impedenze in funzione della frequenza, se desiderato o conveniente. Le formule necessarie sono riportate in Rif. 3. Naturalmente è necessario il supporto di un qualche programma di calcolo, essendo impensabile calcolare manualmente la conversione S verso Z per ogni valore di frequenza.
PARAMETRI S PER ALCUNE SEMPLICI RETI
Affrontando oggi un nuovo argomento tecnico, l’approccio ideale vedrebbe simulazioni e misure di laboratorio a conferma delle stesse, affiancare l’indispensabile studio in classe o su testi. Purtroppo il costo dei software di simulazione professionali e della strumentazione necessaria a supporto dell’argomento qui trattato rendono tale strada impraticabile in molti casi. Non tutti i programmi di simulazione SPICE disponibili gratuitamente supportano l’uso di Parametri-S. È però usabile a tale scopo RFsim99, un programma free in circolazione da vari anni ma ancora molto valido (per la reperibilità vedere rif. 4). Con tale programma, può essere condotto lo studio di alcune reti elementari e reti di cui sia nota la risposta da libri di testo o articoli, al fine di familiarizzare con i parametri S. Alcuni esempi sono presentati nella figura 2, figura 3, figura 4 e figura 5.
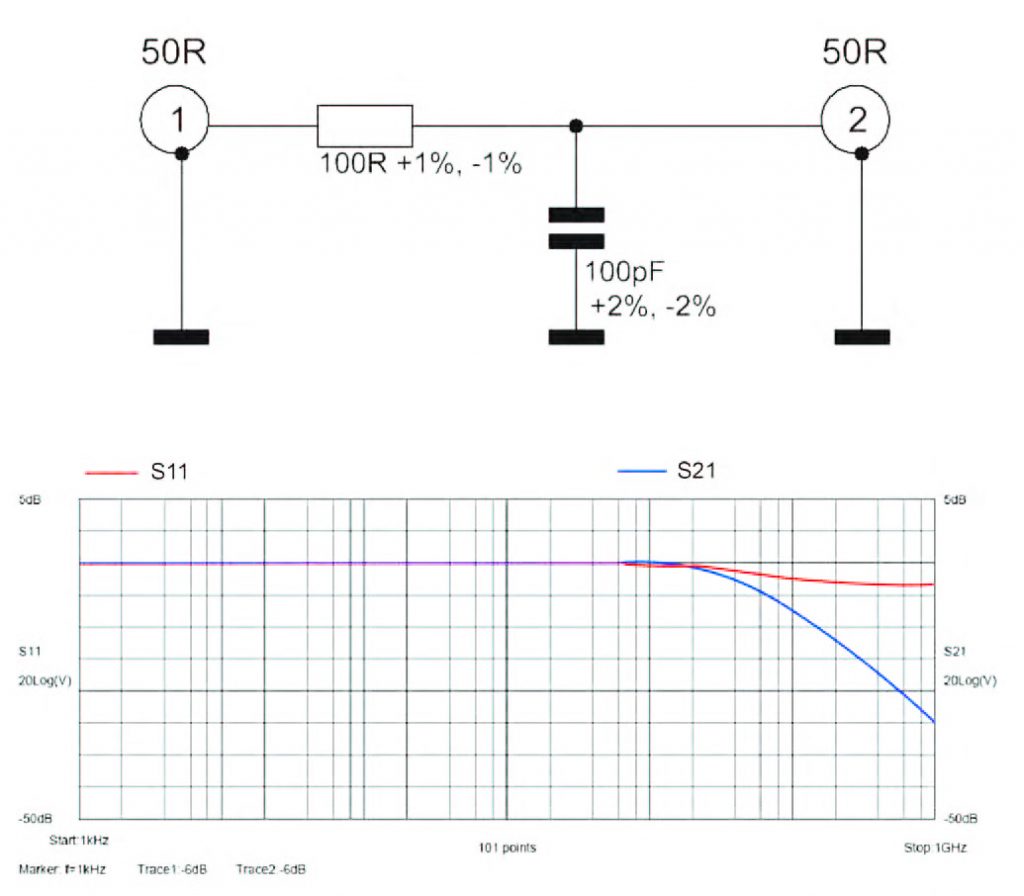
Figura 2: schema e Parametri-S per Rete RC ideale.
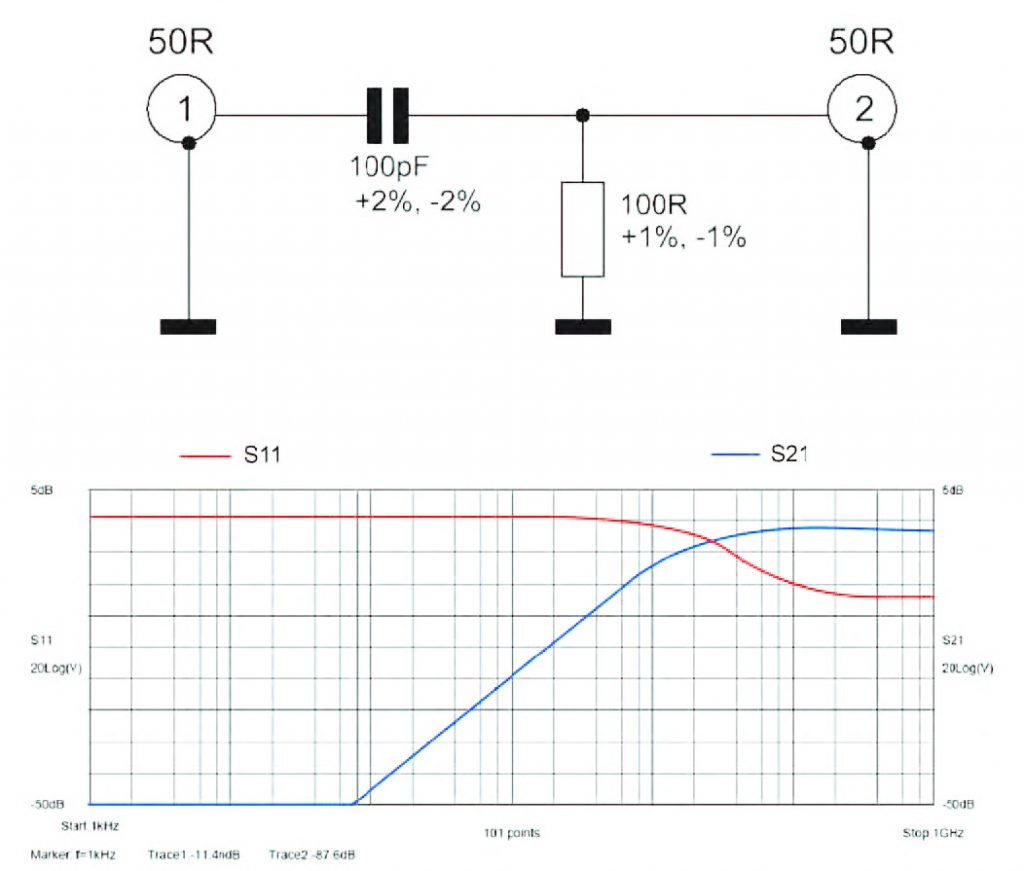
Figura 3: schema e Parametri-S per Rete CR ideale.
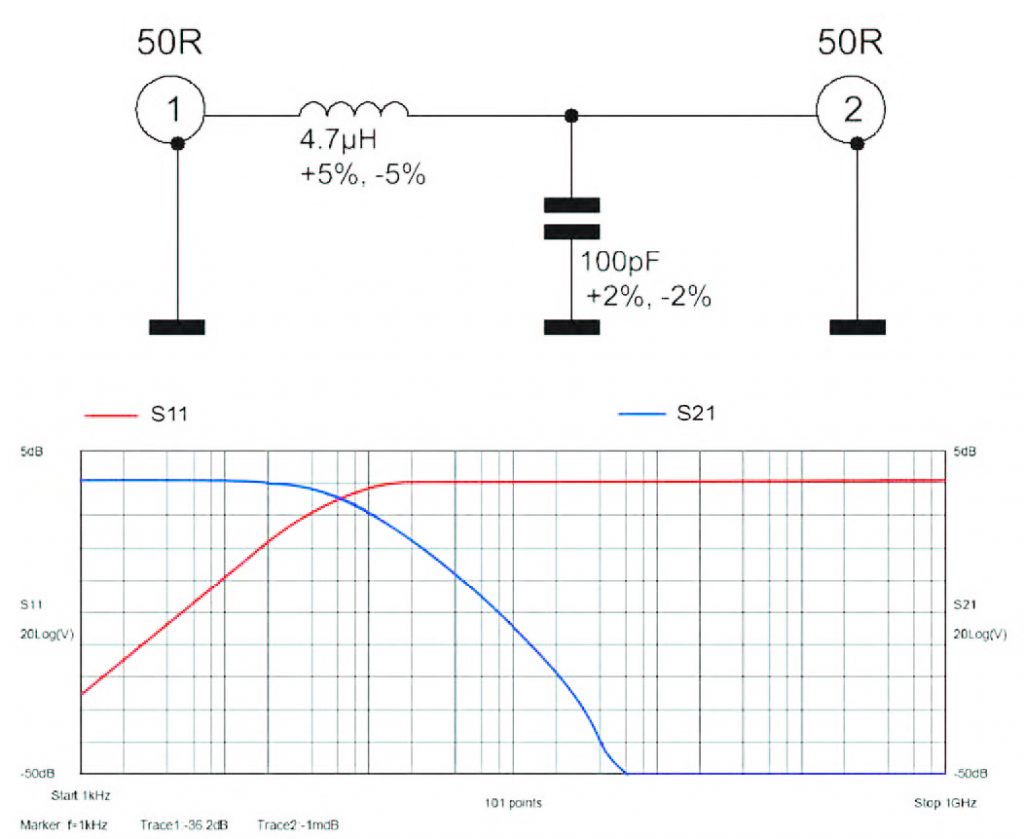
Figura 4: schema e Parametri-S per Rete LC ideale.
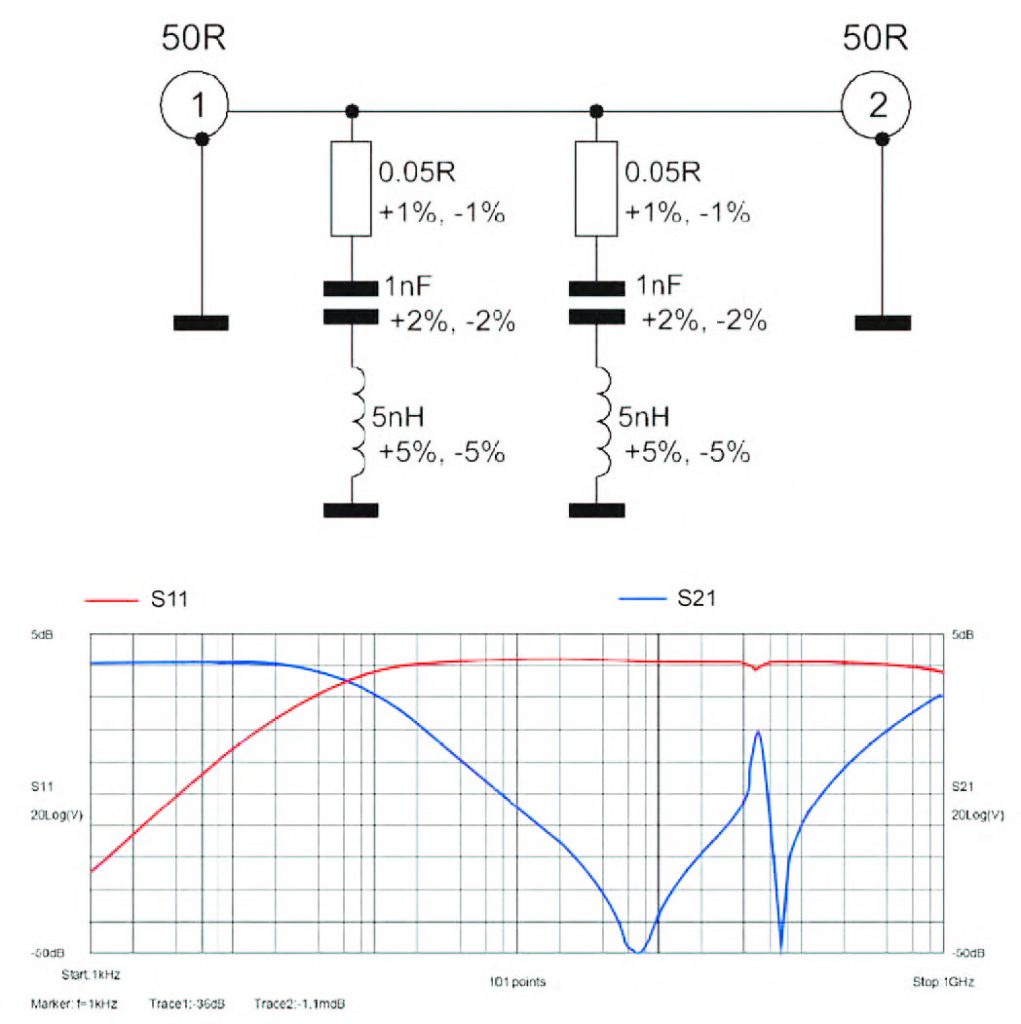
Figura 5: schema e Parametri-S per Condensatori Reali in parallelo 100nF + 1 nF
Come sempre nelle simulazioni, ma in questo caso in particolare, l’accuratezza della modellizazione determina l’accuratezza della risposta ottenuta dal simulatore, come in figura 6. Ad esempio in figura 2, dobbiamo essere ben consapevoli che stiamo considerando componenti ideali, trascurando, tra l’altro, la resistenza e l’induttanza parassite del condensatore o l’induttanza parassita del resistore.

Figura 6: i parametri S possono anche essere misurati con appositi strumenti.





Articolo molto chiaro sulla necessità di considerare la natura ondulatoria dei fenomeni elettrici quando si fa riferimento a dispositivi e ciruiti di dimensioni confrontabili con la lunghezza d’onda dei segnali in gioco.
Ho trovato interessante anche il riferimento al software RFsim99 che non conoscevo.