
Si continua ad assistere a una crescente penetrazione delle applicazioni 3D in tempo reale in molti ambiti applicativi, non soltanto ludici. Nel settore embedded, in particolare, questo è reso possibile dalla disponibilità di architetture a 32 bit a elevate prestazioni ma a bassa dissipazione di potenza, come ad esempio la serie AVR32 di Atmel. Proponiamo un esempio pronto all’uso per i micro AVR32 di Atmel.
Di seguito, in particolare, è descritto un interessante esempio realizzato con tali dispositivi per il rendering di bitmap testuali su un cubo 3D in rotazione. Il riferimento è un’Application Note di Atmel reperibile sul sito web dell’azienda all’indirizzo indicato nei riferimenti al punto [1].
L’applicazione fa utilizzo della scheda di valutazione EVK1101 (figura 1), dotata di microcontrollore UT32UB3B e di un modulo di espansione con codec audio e display LCD di risoluzione 128 x 128 pixel controllato mediante controller Epson S1D5G10. Tale modulo non è purtroppo disponibile in commercio ma ne sono distribuiti gratuitamente all’interno dell’Application Note sia lo schema elettrico sia il layout del PCB unitamente al codice sorgente dell’applicazione di esempio.

Figura 1: la scheda EVK1101 con modulo di espansione per LCD.
Una breve introduzione
Prima di analizzare i dettagli del progetto, è tuttavia necessario introdurre dei concetti di base, alcuni dei quali di natura matematica, per rendere più chiara la descrizione. Innanzitutto vediamo come descrivere una generica rotazione. Indichiamo, rispettivamente, con
![]()
e j l’asse e l’angolo di rotazione, con
![]()
un generico vettore e con
![]()
il trasformato. Il vettore
![]()
rappresentante l’asse di rotazione deve essere normalizzato, ovvero deve soddisfare la relazione
![]()
Si può dimostrare che sussiste la relazione:
![]()
con la matrice M che assume la seguente rappresentazione
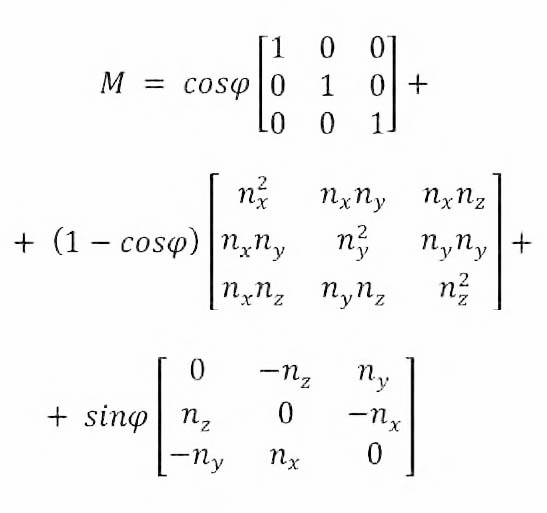
Per semplicità l’esempio di riferimento limita l’asse di rotazione del cubo a uno tra 7 predefiniti. Per quanto concerne la rappresentazione del cubo, supporremo invece per semplicità che il centro coincide con l’origine del sistema di riferimento cartesiano adottato e che questo sia destrorso e orientato in modo tale che l’asse x sia normale al piano di vista dell’osservatore (coincidente con il piano del display LCD). Per visualizzare il cubo è quindi sufficiente conoscere l’insieme delle coordinate dei suoi vertici e l’ordine con il quale queste sono connesse tra loro. Lo schermo adottato ha una dimensione di 120 x 120 pixel. Questo significa che, poiché, come noto, la lunghezza della diagonale di un cubo è data da
![]()
dove l è appunto il lato del cubo, il cubo che potremo visualizzare sullo schermo supportato dalla nostra piattaforma può avere al massimo lato di lunghezza pari a
![]()
pixel. L’esempio di riferimento discusso nell’Application Note che stiamo considerando prevede di poter visualizzare sulle facce di ogni lato del cubo immagini predefinite. Per rappresentare ognuna di queste, è necessario memorizzare per ogni suo pixel la posizione nello spazio 3D e il relativo colore. Con uno schermo di bassa risoluzione, come quello selezionato, è sufficiente rappresentare ogni coordinata della posizione del pixel mediante un singolo byte. In particolare, l’esempio di riferimento che stiamo considerando utilizza un array di char signed (dal momento che le coordinate possono assumere evidentemente anche valori negativi) per definire un generico oggetto 3D; l’array ha dimensione di 3 x npoints, dove npoints è il numero di punti necessari appunto alla rappresentazione dell’oggetto. L’array contiene ordinatamente le coordinate x di tutti punti, quindi quelle y e infine quelle z. Allo stesso modo, per semplicità, viene supposto di codificare l’informazione di colore di ogni pixel su soli 8 bit, riservando 3 bit per l’intensità della componente di rosso, 3 per quella di verde e 2 per quella di blu. In totale, quindi, la rappresentazione dell’immagine di una faccia del cubo richiede al massimo 14,4 Kbyte di memoria dati. Per rappresentare invece in memoria l’immagine 2D (risultante dalla proiezione del cubo 3D) che viene infine visualizzata sullo schermo, è sufficiente definire un vettore di char (questa volta unsigned) di dimensioni pari a quella del display (ovvero 120 x 120 pixel). Ogni elemento del vettore rappresenterà, infatti, il colore del relativo pixel sull’LCD. Nel codice di esempio dell’Application Note discussa, l’array è chiamato RASTER.
RENDERING IN QUATTRO MOSSE
L’esempio di riferimento discusso nell’Application Note che stiamo considerando utilizza il joystick presente a bordo della scheda EVK1101 per selezionare l’asse di rotazione del cubo; utilizzando i pulsanti destro e sinistro è possibile cambiare la selezione corrente tra i valori predefiniti. L’accelerometro, anch’esso disponibile sulla scheda, è utilizzato invece per impostare l’angolo di rotazione, il cui valore, d’altra parte, determina direttamente la velocità con la quale si vede ruotare il cubo sullo schermo. Spostando verso l’alto la scheda si incrementa l’angolo di rotazione, spostandola verso il basso lo si riduce. Il listato 1 riporta un estratto del codice sorgente della funzione main() dell’applicazione di esempio mentre la figura 2 ne ricostruisce in modo semplificato il corrispondente diagramma di flusso.
int main(void)
{
int i = 0; int teta = 0; int MYTSFMATR[9];
// First init of the rotation matrix
mrot_C8_FULL_FFIX(MYTSFMATR, teta, 0x5A82, 0x5A82, 0);
// Initialize LCD_NOKIA resources: GPIO, SPI
lcd_nokia_resources_init();
// Controller initialization routine for LCD controller
lcd_nokia_init();
// Init Joystick Service
DV_JOYSTICK_Init();
// Init Accelerometer Service
DV_ACCELEROMETER_Init();
reset_Raster(RASTER);
for (;;) {
gpio_tgl_gpio_pin(LED1_GPIO);
//Call the Joystick tasks
DV_JOYSTICK_Task();
//Call the Accelerometer tasks
DV_ACCELEROMETER_Task();
//modify rotation axes
switch (rotation_axes_cpt)
{ … }
// Teta Update: Update step between every rotation axes
teta += Ball_speed;
if(teta>=240)
{ teta=0; }
// Display Screen
SEND_RASTER_BUF(RASTER);
// Clear Display Buffer for next compute step
reset_Raster(RASTER);
// Compute 3D Transformation with last MATRIX value
// Input buffer : centers / Output buffer : tmpcenters
transforme_C8_FFIX((OBJ3D_C8_FFIX *)¢ers, (OBJ3D_C8_FFIX
*)&tmpcenters, (int *)MYTSFMATR);
// Compute zBuffer Transformation in order to optimize display
update_faces();
for( i = 0; i < Number_Face_to_print; i++)
{
// Test if it is a face to display so a Picture
if (cube_logoavr32[Face_to_prints[i]])
{
transforme_C8_FFIX(cube_logoavr32[Face_to_prints[i]],
tmpcube_logoavr32[Face_to_prints[i]], MYTSFMATR);
draw_image_raster_bmp(tmpcube_logoavr32[Face_to_prints[i]],
AVR32_COLOR, RASTER);
}
// Else Display Cube Transformation
transforme_C8_FFIX((OBJ3D_C8_FFIX *)&of[Face_to_prints[i]],
(OBJ3D_C8_FFIX *)&tmpof[Face_to_prints[i]], (int *)MYTSFMATR);
draw_image_raster(&tmpof[Face_to_prints[i]], MESH_COLOR, RASTER);
}
}
}
| Listato 1 |
Le funzioni DV_JOYSTICK_Task() e DV_ACCELEROMETER_Task() gestiscono le corrispondenti periferiche di controllo secondo quando descritto in precedenza. Per quanto concerne le funzioni di visualizzazione, invece, come si vede dalla figura 2, il programma esegue (riga 29) dapprima il refresh dell’immagine del cubo sullo schermo, utilizzando l’interfaccia SPI del controller dell’LCD. Quindi (riga 31) ripulisce l’intera immagine in memoria e calcola (riga 34) la nuova posizione dei centri delle facce. Infine confronta questi per determinare le facce che devono essere visualizzate. A questo scopo, come detto, per semplicità, sono previsti solo 7 assi di rotazione predefiniti e questi sono inoltre scelti in modo da semplificare il task di rappresentazione del cubo sullo schermo. E' sufficiente, infatti, calcolare la coordinata z del centro di ogni faccia e confrontare i valori trovati per identificare le tre facce del cubo da rappresentare; questo compito è svolto dalla funzione update_faces(). Se la faccia da visualizzare contiene un'immagine (riga 40) ne viene calcolata la trasformata (riga 42) a seguito della rotazione imposta. Quindi questa viene copiata (riga 43) nel buffer di memoria (l'array RASTER) che rappresenta l'immagine 2D da visualizzare sullo schermo LCD. Poichè il sistema adotta un riferimento cartesiano con asse x normale al piano di visione dell'utente, come detto, la trasformazione dell'immagine 3D in immagine 2D può essere ottenuta mediante semplice proiezione ortografica (per un'introduzione alle diverse tecniche di proiezione 3D si rimanda alla voce [2] indicata nei riferimenti). Dopo aver aggiornato nel buffer video le immagini corrispondenti alle tre facce da visualizzare, il programma procede infine a tracciare le linee che delimitano ognuna di esse. Dapprima calcola (riga 46) i punti trasformati per rotazione dei vertici di ogni faccia, quindi (riga 47) traccia le linee mediante un semplice algoritmo di rasterizzazione DDA (Digital Differential Analyzer), descritto ad esempio in [3].
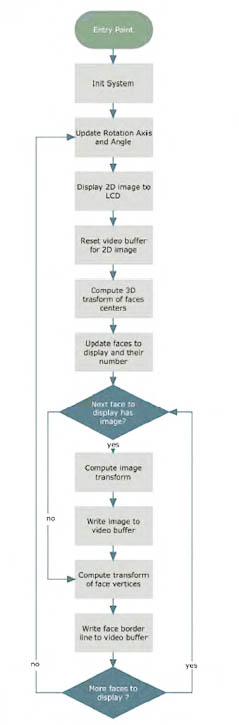
Figura 2: diagramma di flusso del programma di rendering




