Leggendo l’articolo “Generatore di corrente costante con LM317” e i relativi commenti mi sono venute in mente tutte quelle reminescenze sulla logica combinatoria e così ho ben pensato di scrivere due righe sulle “Mappe di Karnaugh”, utilissimo strumento nella progettazione di circuiti in logica combinatoria ma che aimè è caduto quasi del tutto in disuso dopo l’avvento dei microcontrollori a basso costo.
Perché le mappe di Karnaug?
Partendo dal presupposto che siamo tutti a conoscenza della logica binaria e dei relativi operatori (AND, OR e NOT), lo scopo delle mappe di Karnaugh è quello di ridurre al minimo una funzione logica a partire dalla tabella della verità del nostro sistema. Se per esempio il nostro sistema che vogliamo costruire deve rispettare la seguente tabella della verità:
andando ad adottare per ogni “1” dell’uscita una “AND” con gli ingressi negati se il suo valore è uguale a “0” e diretti se uguale a “1”, la funzione che implementa quella tabella logica sarà:
Y = A’B’ + AB’
In realtà, come possiamo vedere dalla tabella di verità stessa, l’uscita è semplicemente l’ingresso “B” negato:
Y = B’
Questa operazione di semplificazione (in questo caso è sufficientemente intuitiva ma quando il sistema ha 3 o 4 variabili di ingresso la tabella di verità si complica e non sempre questa operazione di semplificazione risulta immediata) può essere realizzata con facilità tramite le mappe di Karnaugh.
Come si costruiscono le mappe di Karnaugh?
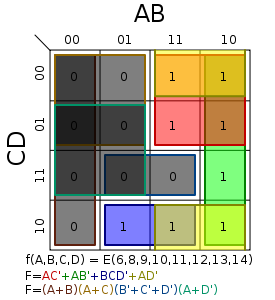
Le mappe di Karnaugh sono costruite mediante la rappresentazione grafica a tabella la quale dovrà contenere un numero di celle pari al numero di combinazione della tabella della verità e in ogni cella verrà inserito il valore assunto dalla “Y” (ossia l’uscita del nostro sistema). A questo punto non resta che raggruppare il massimo numero (che deve essere una potenza di 2) di termini adiacenti che hanno lo stesso valore e quindi formulare opportunamente l’operazione logica considerando solo le variabili che non cambiano di valore all’interno del raggruppamento in considerazione. Le variabili di ingresso del nostro sistema dovranno essere sistemate ai lati della mappa di Karnaugh e le combinazioni dei bit devono avere distanza di Hamming pari a “1”. Detto a parole sembra complicato ma in realtà non è così e lo si può capire se si considera il seguente esempio rappresentato dalla seguente tabella di verità (questa volta è più complessa della precedente):
Come detto in precedenza la mappa di Karnaugh dovrà avere un numero di celle pari al numero di combinazioni che in questo caso è pari a 16, quindi dovrà essere composta da due lati 4x4:
Il raggruppamento deve essere eseguito considerando il massimo raggruppamento possibile di “1” o di “0” adiacenti facendo attenzione però che il numero di elementi raggruppati sia una potenza di 2 (1, 2, 4, …). Sono considerati elementi adiacenti anche quelli della prima e dell’ultima riga o colonna (intuitivamente si può considerare la mappa di Karnuagh come se fosse un “toro”, in cui l’ultima riga o colonna è adiacente con la prima). Ogni raggruppamento produrrà delle “AND” logiche sugli ingressi “AND” nel caso del raggruppamento degli “1” oppure delle “OR” logiche sempre sugli ingressi nel caso di raggruppamento degli “0”; queste operazioni così ottenute dovranno essere sommate tra di loro (OR) se nel caso di raggruppamento degli “1” o moltiplicate tra di loro (AND) nel caso di raggruppamento degli “0”. In fine dovranno essere scelti solo gli ingressi che non cambiano il loro valore all’interno del raggruppamento, considerandoli: nel caso di raggruppamento degli “1” diretti se il valore che non cambia è “1” e inversi se il valore che non cambia è “0”; nel caso di raggruppamento degli “0” inversi se il valore che non cambia è “1” e diretti se il valore che non cambia è “0”. Nel nostro caso sono stati raggruppati gli “1” e la funzione logica che ne risulta viene ricavata nel seguente modo:
Raggruppamento 1: la variabile “A” all’interno del raggruppamento rimane al valore “1” quindi andrà nell’equazione finale; la variabile “B” all’interno del raggruppamento cambia valore e quindi verrà scartata; la variabile “C” all’interno del raggruppamento rimane al valore “0” quindi andrà nell’equazione finale come negata; la variabile “D” all’interno del raggruppamento cambia valore e quindi verrà scartata. Questo raggruppamento produrrà la seguente equazione: AC’.
Raggruppamento 2: la variabile “A” all’interno del raggruppamento rimane al valore “1” quindi andrà nell’equazione finale; la variabile “B” all’interno del raggruppamento cambia valore e quindi verrà scartata; la variabile “C” all’interno del raggruppamento cambia valore e quindi verrà scartata; la variabile “D” all’interno del raggruppamento rimane al valore “0” quindi andrà nell’equazione finale come negata. Questo raggruppamento produrrà la seguente equazione: AD’.
Raggruppamento 3: la variabile “A” all’interno del raggruppamento cambia valore e quindi verrà scartata; la variabile “B” all’interno del raggruppamento rimane al valore “1” quindi andrà nell’equazione finale; la variabile “C” all’interno del raggruppamento cambia valore e quindi verrà scartata; la variabile “D” all’interno del raggruppamento rimane al valore “0” quindi andrà nell’equazione finale come negata. Questo raggruppamento produrrà la seguente equazione: BD’.
Raggruppamento 4: essendo un raggruppamento unitario tutte e 4 le variabili non cambiano valore e quindi l’equazione prodotta da questo raggruppamento sarà A’B’CD. L’equazione finale sarà data dalla somma delle 4 equazioni ottenute e sarà:
Y = AC’ + AD’ + BD’ + A’B’CD
La funzione così ottenuta si dice minima ossia è quella funzione che fornisce l’uscita desiderata con il minor numero di termini e quindi richiede il minor numero di porte logiche. Se fosse stato eseguito il raggruppamento per gli “0” piuttosto che per gli “1” l’equazione finale sarebbe stata:
Y = (A’ + C’ + D’) (A + B’ + D’) (A + B + C) (A + B + D)
Se scriviamo la mappa di Karnaugh per l’esempio fatto inizialmente, vediamo subito che l’equazione del sistema è proprio uguale a Y = B’. Per sistemi con un numero di variabili di ingresso maggiore di 4 la mappa di Karnuagh risulta difficile da usare in quanto è necessaria una rappresentazione tridimensionale oppure si considerano due mappe di Karnaug uguali ma con la differenza che la prima ha la quinta variabile settata ad “0” e la seconda ad “1”; nel momento del raggruppamento se ci sono raggruppamenti tra le due tabelle la quinta variabile verrà scartata, altrimenti deve essere considerata opportunamente. Lo stesso procedimento vale anche per 6 o più variabile, condizione che però rende sempre più complicata l’applicazione della mappa di Karnaug.


Una piccola nota, che mi sono dimenticato di aggiungere all’articolo, riguarda i teoremi di De Morgan che possono essere sintetizzati dalle seguenti uguaglianze:
(AB)’ = A’ + B’
(A + B)’ = A’B’
grazie a queste due equazioni combinate assieme ad un po’ di abilità nelle operazioni logiche, è possibile trasformare le “somme di prodotti” ricavabili dalle mappe di Karnaugh raccogliendo gli “1”, in prodotti di somme ricavabili sempre dalla mappe di Karnaugh raccogliendo gli “0”.
Siccome questi due teoremi sono duali, posso sfruttarli per eseguire la trasformazione inversa ossia posso trasformare i prodotti di somme ricavabili sempre dalla mappe di Karnaugh raccogliendo gli “0” in “somme di prodotti” ricavabili dalle mappe di Karnaugh raccogliendo gli “1”.
ormai e’ tutto automatizzato: esistono degli EDA di vari vendors che, da una descrizione ad alto livello che puo’ essere un linguaggio tipo verilog, vhdl, system c o anche diagrammi di flusso e tabelle di verità, generano una interconnessione di porte logiche. Sicuramente alla base di questi tools ci sono algoritmi che usano la teoria dell’algebra di Boole, ma non bisogna piu’ giocare con le mappe di Karnaugh che rimangono un utile strumento didattico. Questo non vuol dire che incito a non sapere la teoria, ma volevo solo sottolineare che esistono questi tools per la sintesi di reti sia combinatorie che sequenziali. Come molti altri che ne permettono la simulazione funzionale. Comunque articolo conciso, ma efficace.