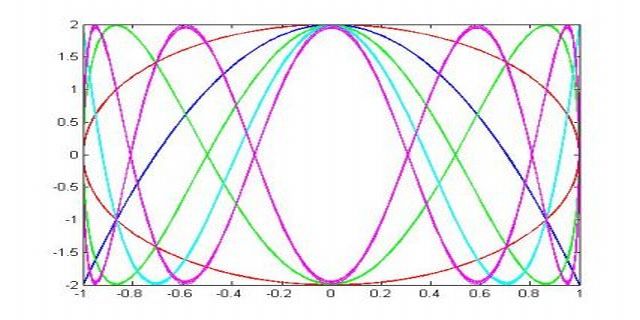
Tra le molte funzionalità che MATLAB offre vi è sicuramente una semplice quanto potente gestione della grafica. Per rimanere in ambito elettronico, in questo articolo mostriamo come disegnare le figure di Lissajous, come particolare applicazione delle proprietà grafiche di MATLAB. Chi si occupa di elettronica, soprattutto di misure ed elaborazioni di segnali, ha probabilmente avuto a che fare con queste “misteriose” figure generate su un oscilloscopio, utili a dedurre il rapporto tra le frequenze, o anche la fase relativa, di segnali sinusoidali. Cercheremo, allora, di dare una visione più generale di queste curve, vedremo qualche possibile applicazione ed infine mostreremo come utilizzare MATLAB per visualizzarle.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 1436 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.
Ti potrebbe interessare anche:
#5 Schede di sviluppo per soluzioni audio
Progettiamo i nostri filtri con FilterPro della Texas Instruments
Linee guida per la progettazione di PCB nelle applicazioni a microonde e millimetriche
Progetto di un robot di Telepresenza con l’ESP32-CAM – Parte 4
Propulsione e Potenza nello Spazio
Dopo tanto tempo che lo avevamo annunciato, finalmente questo articolo è uscito 🙂
Tra la normale organizzazione di questa rivista e qualche imprevisto, è ora disponibile per tutti voi.
Io ci tengo tanto a ringraziare personalmente l’autore perchè l’idea di come è nato questo articolo è stupenda: si tratta di uno dei nostri lettori ed utenti più attivi e coscienziosi.
Lui è la dimostrazione di come faccia questa comunità ad essere sempre così viva, vivace ed attiva.
Ha fatto un’esperienza, si è proposto per condividerla con noi, alcuni hanno mostrato interesse, altri meno, si è decido di pubblicarla e dargli il giusto spazio ed ora, che l’ha voluta condividere con tutti noi, è online.
Un fulgido esempio di cosa sia l’Open Source e di come questa comunità ne faccia un baluardo.
Grazie.
Ottimo lavoro!
Ne approfitterò per chiedere subito se intende pubblicare altro su MATLAB 😉
E suggerisco a tutti voi di far domande e richieste 🙂
L’uso della matematica nella progettazione elettronica è fondamentale e quindi MATLAB, come rappresentazione semplificata delle funzioni matematiche non deve essere sottovalutato anche in questo settore.
A me è stato molto utile nel calcolo della parzializzazione dell’onda sinusoidale in un progetto di una centrale di automazione cancelli con frizione elettronica. Le regolazione della potenza è stata abbastanza semplice grazie a Matlab. Poi l’ho utilizzato nella gestione dei movimenti di una poltrona per le first class dell’AIRBUS A380 in quel caso la situazione è stata molto più complessa in quanto ho dovuto ricorrere alla cinematica inversa.
Anche nelle applicazioni Real-Time Matlab assume un ruolo fondamentale grazie a Simulink, un tool integrato in Matlab che consente di realizzare applicazioni real-time. In questi ultimi anni Mathworks ha trovato il modo per avvicinarsi al mondo dei Field Progammable Gate Array proprio attraverso Simulink. Grande importanza sta assumendo l’elaborazione di segnali numerici, e la richiesta di velocità di elaborazione sempre maggiori ha portato alla necessità di superare i tempi richiesti dai software per eseguire le routine, e ci si è orientati verso l’utilizzo di FPGA. In questo Mathworks ha fatto un passo importante: Simulink con generazione automatica di codice VHDL. Questo rappresenta una svolta per tutti coloro che hanno sempre utilizzato Simulink, ma anche per chi ha sempre utilizzato il VHDL per disegnare FPGA.
Buongiorno a tutti, ottima idea di segnalare qualche esercizio su matlab, ma sinceramente, visto che si parla di opensource, strizzerei l’occhio anche a scilab o simili!!
Sulla sua osservazione ci sarebbe tanto da dire.
Innanzi tutto il concetto di OpenSource, e della possibilità, o utilità, o “coerenza” di questo sito riguardo la pubblicazione di post relativi ad alle applicazioni che si possono fare con MATLAB (che, appunto, non è opensource) è stato già ampiamente discusso in calce ad altri post simili (precedentemente i miei) ma le riporto le mie considerazioni, che mi hanno spinto a *condividere* le *mie* conoscenze:
1. Quello che legge nell’articolo, prima della prima riga di codice, è del tutto generale e prescinde dal software usato per realizzarlo in pratica, quindi va bene anche con SCILAB (tra l’altro i comandi sono molto simili ed esistono addirittura dei programmi per la conversione del codice, ma non so quanto siano affidabili).
2. Io so usare MATLAB e condivido in maniera aperta (OPEN!) con chi è interessato, il *mio* modo di risolvere dei problemi con MATLAB (anche banali, se vogliamo, ma non credo che descrivere come implementare un simulatore real-time di un sistema di trazione ferroviaria con generazione automatica di codice per FPGA possa essere di interesse di tutti)
3 MATLAB è presente in quasi tutti i corsi universitari di Ingegneria dei sistemi o controlli, quindi degli esempi applicativi posso essere utili agli studenti
4 MATLAB dispone di una comunità “aperta” (sul sito della mathworks) dove chiunque può condividere dei file o suggerire soluzioni a problemi altrui
5 con MATLAB è possibile sviluppare applicazioni OPEN SOURCE, infatti esistono delle librerie (open e free) per interagire con ARDUINO e programmarlo (non so se esiste un equivalente con SCILAB)
Se me lo concede, le propongo dei contro-esempi: forse in questo sito non si può descrivere come fare una misura con un oscilloscopio, visto che lo schema dello stesso non è “open”? Oppure (e se sbaglio accetto umilmente le correzioni) non mi sembra che il core dei microcontrollori (ad esempio ARM), cioè l’oggetto da usare, sia open, eppure si insegna lo stesso come programmarli; semmai sono open le schede che usano questi componenti.
In sintesi: open è il contenuto, non il contenitore!
E per finire, se c’è qualcuno che conosce SCILAB o OCTAVE è chiaramente inviato a condividere le sue conoscenze con noi. Io non tempo da dedicare allo studio di un ulteriore ambiente di lavoro, ma leggere qualche articolo ed imparare qualcosa non mi dispiacerebbe. Io, compatibilmente con il mio tempo libero, cercherò di produrre ulteriori articoli, sperando che gli argomenti (indipendentemente dalla piattaforma) possano essere utili ed interessanti per i lettori.
La mia non voleva affatto esser una critica. Ma venendo dal mondo universitario appunto dove un po si bazzica con matlab, era il modo di dare un input anche verso altri programmi, che come ha sottolineato, alcuni sono molto ben integrabili con MATLAB. Fermo restando che, per quanto sia buono un programma come OCTAVE o SCILAB, ho avuto modo di trovarmi alcuni problemi come l’affidabilità sul troncamento o piccolezze del genere! Ovviamente leggo con molta attenzione i Vostri post, i progetti che vengono presentate.