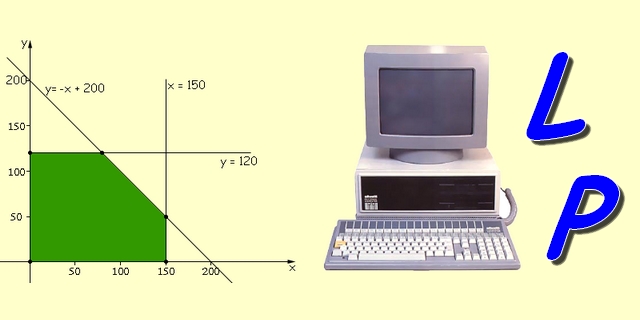
Scopriamo il funzionamento di un semplice ed utile programma, finalizzato alla risoluzione dei problemi di ottimizzazione, connessi alla ricerca dell’ottimo, per minimizzare e massimizzare i risultati. Aziende, compagnie di voli, scuole, agenzie di trasporti e laboratori utilizzano in maniera intensiva la programmazione lineare, per sfruttare al meglio le proprie risorse al minor costo possibile.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 1052 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.








Ciao, ho letto con interesse questo ed altri articoli di altri autori riguardanti la programmazione matematica e vi faccio i complimenti per la chiarezza nell’esposizione.
Volevo sapere se fosse possibile usare il GNU Linear Programming Kit (o simili) per ottimizzare la scelta dei componenti per la realizzazione di progetti elettronici.
Considerando che le variabili in gioco sono molte (prezzo unitario, numero di componenti minimo dell’ordine, spese di spedizione, variazioni di prezzo in base agli articoli in stock, affidabilità del distributore, etc…), immagino che questa per il progettista sia una abilità che si acquisisce con l’esperienza piuttosto che una competenza che si può acquisire in “modo teorico”.
Essendo alle prime armi nella progettazione elettronica,e quindi con poca esperienza, mi chiedevo se ci fosse qualche tool che sia di aiuto in questo senso.
Salve e grazie del commento.
La formalizzazione di un problema in un obiettivo è spesso estremamente complesso. Pertanto, qualsiasi tool si utilizzi, occorre avere le idee estremamente chiare su come impostare il problema e le sue variabili, nonché i limiti, le condizioni e altro.
Il mio consiglio è quello di utilizzare (almeno all’inizio) il programma che ho proposto, impostando inizialmente un problema estremamente semplice (nel suo caso inserisca, ad esempio, solo il numero di componenti ed i costi).
Man mano che visualizza i risultati, provvederà poi a complicare le cose, aggiungendo nuovi parametri e nuove variabili.
PS.
Sto preparando un software per risolvere questa tipologia di problemi, tramite metodo Montecarlo….
Giovanni
Ti dico sinceramente che cosa penso: la cosa migliore è imparare partendo da progetti molto semplici e fare proprio questi ragionamenti su tutti i componenti.
Man mano che guadagni pratica sei anche più in grado di guardare al numero di componenti o al tipo di componenti con occhio critico.
Penso che sicuramente ci sia un modo per fare questo genere di valutazioni in maniera automatizzata ma nulla può sostituire l’esperienza ed il valore inestimabile della pratica. 🙂
Fatti guidare dalla logica all’inizio piuttosto che da un software! 🙂
Detto questo,però, sono sicuro che l’autore potrà essere molto più utile e preciso di me 🙂