Studio dell'Oscillatore a ponte di Wien
Oscillatore a ponte di Wien: introduzione
L' articolo è strutturato per permettere il confronto diretto tra i vari oscillatori dei prossimi articoli. Lo scopo di questo articolo è quello di analizzare, con modellazione matematica, simulazione circuitale e successiva implementazione, un circuito oscillante molto semplice e noto, chiamato Oscillatore a ponte di Wien.
La trattazione di questo oscillatore rimane comunque molto semplificata, ma volutamente dato che si vuole fornire le basi per capire il funzionamento e le principali caratteristiche. L'elaborato si sviluppa in diversi passi:
-
- La caratterizzazione matematica porterà a trovare i valori dei componenti da utilizzare rispettando le specifiche date.
- La simulazione mediante ALTIUM DXP 2006 permetterà di analizzarne le caratteristiche del transitorio e del regime sinusoidale.
- Il confronto tra la simulazione ed il circuito fisicamente realizzato.
- L'implementazione del circuito stampato.
Questo oscillatore fa parte della categoria di oscillatori Armonici o più propriamente quasi sinusoidali.
Questo oscillatore basa il suo funzionamento sul circuito a ponte di Wien elaborato da Max Wien nel 1891. All'epoca di Wien non erano ancora stati inventati dispositivi attivi, in grado cioè di amplificare, e l'oscillatore non poté essere realizzato. [Tratto da Wikipedia]
Come sarà possibile osservare pero' quest'oscillatore non presenta delle belle caratteristiche per un reale utilizzo pratico, ma analizzarlo consente di capire le basi di oscillatori utilizzati in molti campi dell'elettronica che basano il loro principio proprio su questo oscillatore.
Analisi Matematica dell'oscillatore a ponte di Wien
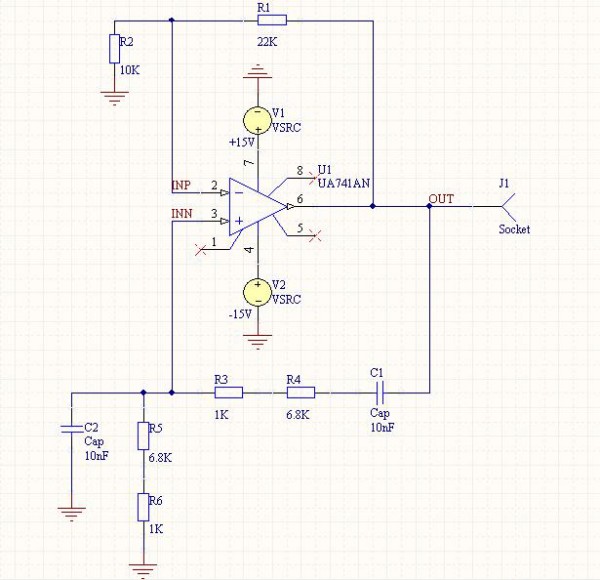
L'Illustrazione 1 riporta lo schema circuitale dell'oscillatore di Wien, dal quale si può constatare la semplicità nella costruzione. Il circuito fa uso di un amplificatore operazionale, il generico UA741, impostato in configurazione NON INVERTENTE e presenta, sul ramo di retroazione, OUT-INN, una rete RC che permette di avere un'oscillazione del segnale.
Non ci sono ulteriori differenze rispetto ad un amplificatore in configurazione invertente, viene alimentato con tensione duale [-15 , +15] V e presenta una serie di resistenze per rammentare che non tutti i valori sono reperibili in commercio.
Generalmente un amplificatore, che sia in configurazione non invertente che invertente, presenta una retroazione di segno negativo che permette di non fare divergere l'uscita, invece oscillatore sfrutta il principio per il quale il rischio di racchiudere l'amplificatore in un anello di retroazione sul quale sono presenti componenti non lineari, per qualche frequenza, può portare la retroazione a passare da negativa a positiva.
In queste condizioni il solo rumore nel circuito dato ad esempio dalla presenza di rumore termico o dalle non idealità dei vari componenti, se amplificato, innesca un'oscillazione che risulta essere divergente.
Per invertire il segno della retroazione del sistema, quello che si fa è sfasare il segnale in uscita di 180°, ponendo in anello chiuso, tra OUT-INN, una rete RC. Questa rete oltre a permettere lo sfasamento del segnale, definisce anche la frequenza di risonanza dell'oscillatore data dalla seguente relazione:

Quindi dalla Formula 1, imponendo una frequenza di oscillazione da noi scelta ![]() ed un valore di capacità facilmente reperibile, si ricava la resistenza appropriata:
ed un valore di capacità facilmente reperibile, si ricava la resistenza appropriata:

Il valore trovato in Formula 2 però non è presente come valore standard reperibile sul mercato, dunque per approssimarlo al meglio sono state realizzate due serie di resistenze (R3+R4) e (R5+R6).
Passo successivo è il dimensionamento delle due resistenze che compongono la retroazione negativa e stabiliscono il guadagno dello stadio di amplificazione.
La condizione da rispettare per fissare il valore di tali resistenze è quella per la quale l'oscillazione è autosostenuta, che si ha quando il guadagno di anello e' unitario. Altra condizione da soddisfare è relativa all'innesco dell'oscillazione che, come detto precedentemente, è soddisfatta amplificando il rumore di conseguenza ponendo un guadagno di anello leggermente superiore a 1.
Quindi nel caso ideale si dovrebbe prima porre un guadagno leggermente superiore a 1 per innescare l'oscillazione e successivamente porlo pari a 1 per autosostenere l'oscillazione senza amplificare l'onda in uscita e di conseguenza non facendo entrare in gioco le distorsioni date dalla saturazione dell'amplificatore operazionale.
In realtà, con questo circuito, non è possibile avere un guadagno unitario costante e quindi ciò che si fa per soddisfare la condizione più forte, cioè l'innesco, è porre il guadagno superiore a quello unitario.
Ovviamente risulta il guadagno non sarà prossimo al quello unitario dato che potremmo benissimo trovarci ad avere i calcoli esatti ma una retroazione negativa che quindi smorza la retroazione, per questo un guadagno non troppo elevati, per esempio pari a 3, va più che bene, come viene mostrato di seguito:

una giusta scelta del valore di R1 è
![]()
questo perché facilmente reperibile e perché così facendo in guadagno non risulta molto elevato e di conseguenza la distorsione, data dalla saturazione dell'amplificatore, non incide molto sull'onda in uscita.
Simulazione dell'oscillatore a ponte di Wien
Passiamo ora ad osservare il comportamento del circuito oscillante simulandone il comportamento tramite il programma ALTIUM DXP 2006. Nelle simulazioni si è ritenuto interessante osservare il comportamento dell'oscillatore nel transitorio, nel regime stazionario sinusoidale, in frequenza per poter vedere la frequenza di oscillazione e l'incidenza delle armoniche, ed infine una breve e semplice simulazione tramite Monte Carlo Analysis per osservare il comportamento usando componenti con tolleranze.
Analisi Transitoria
Parametri per la simulazione :

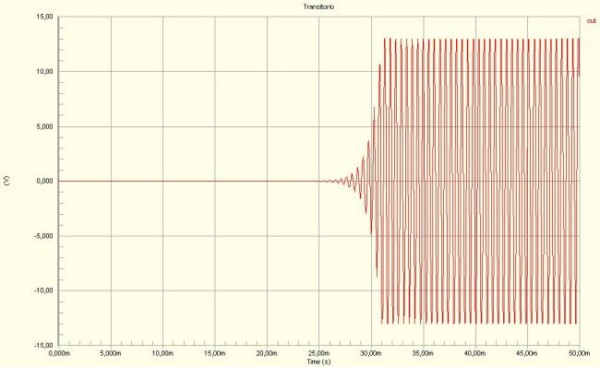
Primo passo dell'analisi dell'oscillatore è la simulazione del comportamento del sistema su un tempo relativamente lungo per poter così osservare la dinamica complessiva data dalla risposta al transitorio e la risposta a regime.
Dall'Illustrazione 2 dopo all'incirca 20ms il rumore diventa apprezzabile per innescare l'oscillazione e portarla a divergere esponenzialmente per poi saturare al valore di tensione di massima dinamica dell'operazionale.
Fase di divergenza
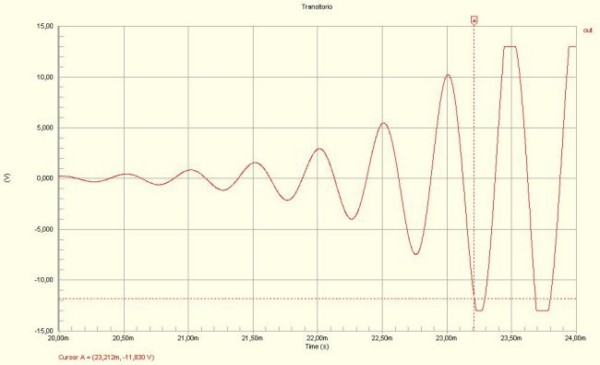
Illustrazione 3: Innesco e divergenza dell'oscillazione
Parametri per la simulazione :

Riportiamo tramite questa simulazione la parete del funzionamento di un oscillatore che non è di facile visione nell'analisi del circuito reale, e cioè la fase di transizione, dall'uscita nulla all'uscita a regime.
Il segnale diverge in maniera esponenziale e considerando il punto in cui l'uscita raggiunge il 90% dell'intera dinamica 11,830 [V], si può osservare che il tempo che si impiega per raggiungere la saturazione 3,21ms.
L'Illustrazione 3 fa vedere proprio come la sinusoide di piccola ampiezza venga, grazie al guadagno di anello superiore a 3, amplificata, diverga ed infine saturi alla tensione di massima dinamica.
Analisi a “Regime”
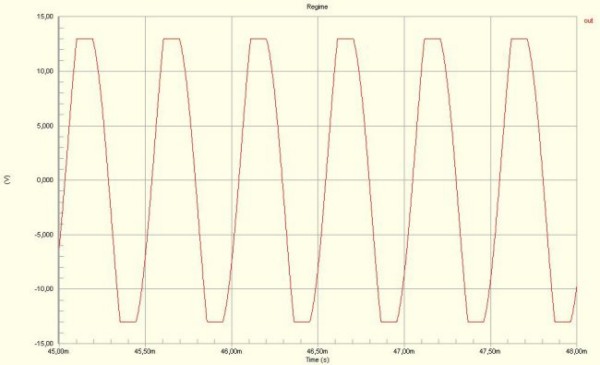
llustrazione 4: Uscita a "REGIME"

In realtà questo sistema non presenterebbe un regime perché si tratta di un Sistema INSTABILE, ma siccome la dinamica del segnale di uscita resta limitata al massimo negli intorni della tensione di alimentazione dell'amplificatore, si può definire il regime quando il segnale in uscita satura.
La forma d'onda in uscita presenta un andamento che si avvicina ad una sinusoide con i picchi tagliati. Dallo studio del datasheet dell'amplificatore operazionale utilizzato UA741 si è constatato che:
-
1.L'uscita può assumere massimo un valore di V
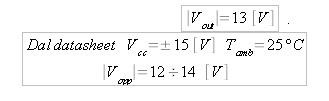
2.L'andamento non sinusoidale non è dovuto all'effetto di Slew Rate.

Spettro del segnale
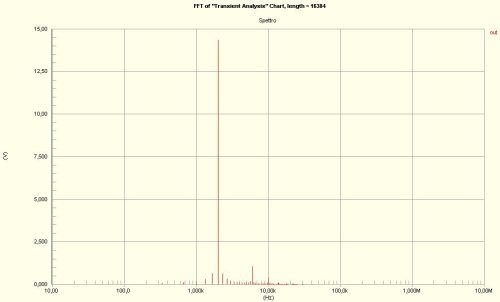
Illustrazione 5: Spettro del segnale in uscita
Parametri per la simulazione:
Tempo di Inizio: 45ms
Tempo di fine: 48ms
Passo di analisi: 0,1μs
N° campioni: 16384
Per effettuare quest'analisi si è ritenuta una buona risoluzione quella di usare un passo di analisi pari a 1μs dato che:

Ed inoltre prendendo una finestra da 3ms il calcolo della FFT risulta essere bene approssimato dato che:
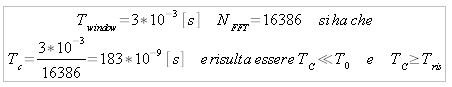
L'analisi dello spettro del segnale ci porta ad osservare che, la frequenza di oscillazione si attesta su quella data da specifica.
Armoniche della frequenza di risonanza
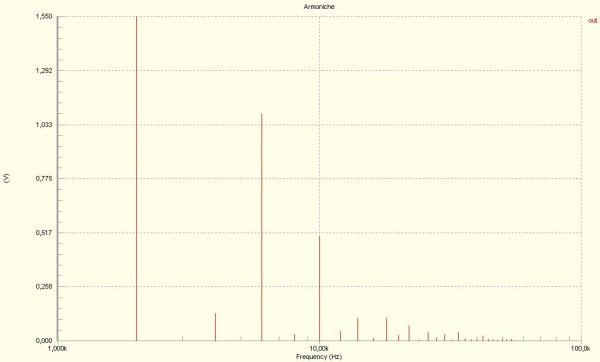
Illustrazione 6: Armoniche della frequenza di risonanza 2,001 [kHz]
Parametri per la simulazione:
Tempo di Inizio: 45ms
Tempo di fine: 48ms
Passo di analisi: 0,1μs
Freq. Centrale: 2001Hz
Una volta trovata la frequenza fondamentale mediante il calcolo della FFT, è possibile effettuare il calcolo della trasformata di Fourie nella frequenza centrale ed osservare le armoniche presenti.
Come si nota le armoniche pari sono più alte delle armoniche dispari.
Da questo grafico si nota come a livello di spettro sia sporco il segnale in uscita e per questo l'utilizzo pratico per molti scopi non e' indicato.
Alcune armoniche che possono essere incidenti sono:
-
1.(Prima) 4,002 [kHz] con ampiezza 100 [mV]
2.(Seconda) 6,003 [kHz] con ampiezza 1,100 [V]
3.(Quarta) 10,005 [kHz] con ampiezza 500 [mV]
4.(Sesta) 12,006 [kHz] con ampiezza 110 [mV]
5.(Ottava) 14,007 [kHz] con ampiezza 120 [mV]
Transitorio Monte Carlo Analysis
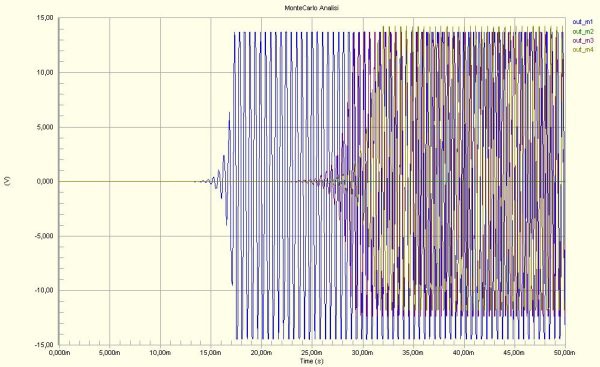
Illustrazione 7: Risposta transitoria con metodo Monte Carlo
Parametri per la simulazione :
Tempo di Inizio: 0s
Tempo di fine: 50ms
Passo di analisi: 10μs
Tolleranze componenti: 10% all
Distribuzione: uniforme
N° test: 4
Il metodo Monte Carlo applicato all'analisi circuitale mi permette di poter analizzare il comportamento de sistema al variare dei valori nominali dei vari componenti sia attivi che passivi. In questo modo è possibile controllare la robustezza del circuito alla presenza di tolleranze nei componenti.
Dall'Illustrazione 7 si può osservare come varia il tempo di risposta e l'ampiezza dell'oscillazione nel considerare componenti con tolleranze. E' interessante osservare come in alcune simulazioni si verifichi uno sbilanciamento della forma d'onda dovuto alle tolleranze, molto eccessive, sulle tensioni di alimentazione.
Spettro Monte Carlo Analysis
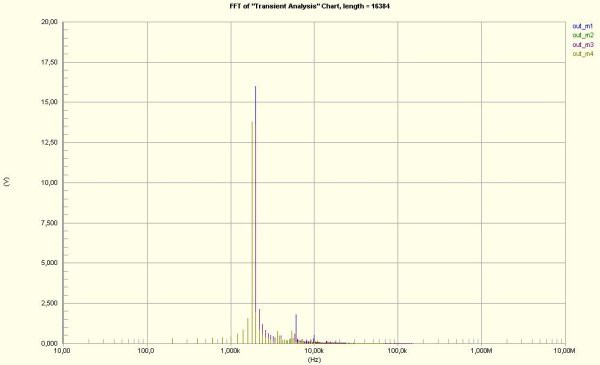
Illustrazione 8: Spettri dell'analisi Monte Carlo
Lo spettro mette in evidenza una particolarità rispetto al caso ideale, ed è la seguente: Con tolleranze del 10% sui componenti della rete di retroazione positiva, ovvero tolleranze sui resistori e condensatori, la frequenza di risonanza può sensibilmente variare arrivando a toccare anche i 200 Hz di differenza.
Prova sperimentale
Successivamente allo studio delle caratteristiche del sistema mediante simulatori, passando alla realizzazione pratica si sono potuti constatare tutte, o quasi, le caratteristiche precedentemente analizzate, ed in particolare:
-
1.Sinusoide in uscita tosata al valore di alimentazione dell'operazionale.
2.Frequenza di oscillazione pari a 2kHz come da specifiche.
3.Aumentando il guadagno dell'amplificatore R2 >>22 la sinusoide in uscita diventa approssimabile ad un onda quadra con periodo pari a 2kHz.
4.Ponendo un guadagno inferiore o uguale a 3 con R2 <20 in uscita l'oscillazione non presente.
Realizzazione PCB
Di seguito sono riportate le viste dei pcb realizzati mediante l'ausilio del convertitore Schematico-PCB di ALTIUM DXP. Data la semplicità delle schede, si è preferito realizzarle su singola faccia con uno spessore di pista di 3 mm.
Altro particolare interessante le piste di massa sono collegate al poligono che circonda la scheda.
Per quanto riguarda i connettori per le alimentazioni, la piazzola che identifica il pin positivo dell'alimentatore ha forma quadrata.
Per realizzarla fisicamente sono stati trasformati i file CAM in GERBER FILE richiesti per l'uso della fresa.
Qui' sotto è riportato il listato dei componenti presenti sulla scheda.

Copyright (c) 2007 Antonio Litterio Cinzia Nicoletti Alessio Rolleri.
E' garantito il permesso di copiare, distribuire e/o modificare questo documento seguendo i termini della Licenza per Documentazione Libera GNU, Versione 1.1 o ogni versione successiva pubblicata dalla Free Software Foundation; con le Sezioni Non Modificabili nessuna, con i Testi Copertina SIMULAZIONE E IMPLEMENTAZIONE DI UN OSCILLATORE A PONTE DI WIEN, e con NESSUN Testo di Retro Copertina. Una copia della licenza è acclusa nella sezione intitolata "Licenza per Documentazione Libera GNU".
Repost: 4 Feb 2009