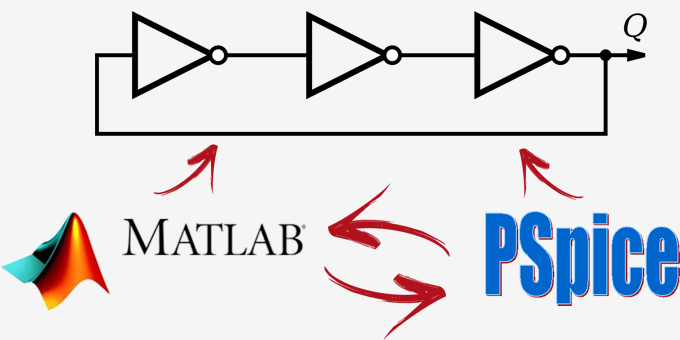
Nella realtà tutti i sistemi fisici sono non lineari e approssimativamente lineari solo per piccoli segnali. Spesso risulta inevitabile considerare una non linearità in un sistema di controllo; non linearità presente nel processo da controllare oppure nella strumentazione. In altri casi si pone una non linearità nel controllore al fine di ricavarne un vantaggio sia in termini tecnici che economici. I dispositivi elettronici più comuni sono caratterizzati da comportamenti (fortemente) non lineari. In caso di non linearità statica ed a simmetria dispari è possibile impiegare il metodo della funzione descrittiva per lo studio dei suddetti sistemi. Un metodo non rigoroso, ma semplice, intuitivo e soddisfacente in molteplici campi applicativi. Scopo dell'articolo, dunque, è mostrare il metodo per poi applicarlo allo studio di un Ring Oscillator con tre stadi di inversione in tecnologia CMOS. Metodo utile ed efficace per la sintesi e l'analisi di generici oscillatori.
Introduzione
Un sistema lineare SISO (Single Input Single Output) strettamente proprio con funzione di trasferimento Γ(s), può essere descritto anche dalla sua relazione minima:
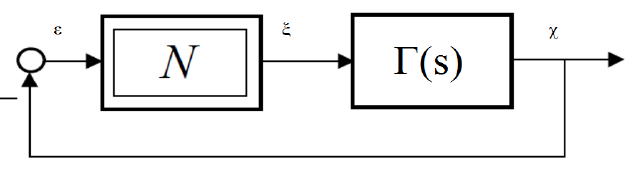
rappresentato in Figura 1 nella sua forma canonica:
Si consideri l'elemento non lineare N, costituito da una funzione ad un sol valore
che soddisfa la condizione
Dunque, l'equazione di stato complessiva è
poiché
Pertanto η=0 è uno stato di equilibrio, visto il rispetto della condizione φ=0.
Diviene indispensabile introdurre - per comprendere quanto sarà illustrato nel seguito - il concetto di stabilità, facente riferimento alla stabilità asintotica, che ha come regione di attrazione l'intero insieme di stato.
Si supponga che lo stato iniziale del sistema assuma un qualunque valore e di domandarsi se il movimento dello stato che ne consegue tenda o meno, in ogni caso, allo stato nullo. Inoltre, si ipotizzi che la funzione ξ(t)=φ(ε(t)) sia parzialmente incerta, ovvero di essa si sa solo appartenere ad una particolare classe funzionale (Φ[k1, k2]) che contiene le funzioni φ che soddisfano
Pertanto la funzione φ(ε) - le dipendenze temporali sono state rimosse per alleggerire la notazione - è compresa tra le due rette passanti per l'origine aventi come equazioni
Si può dunque fornire la definizione di stabilità.
DEF 1: Il sistema canonico è assolutamente stabile nel settore [k1, k2] se lo stato di equilibrio η=0 è globalmente stabile qualunque sia la funzione φ appartenente alla classe Φ[k1, k2].
In questa definizione si entra nel merito della sola parte lineare del sistema, mentre per quella non lineare φ(ε) si ipotizza l'appartenenza ad una classe di funzioni. Tale definizione è sempre valida se non diversamente specificato il settore di riferimento, in quel caso la definizione di stabilità perde di significato.
Per quanto concerne la stabilità assoluta, non ci sono condizioni necessarie e sufficienti. Nel seguito una condizione necessaria ed una sufficiente strettamente legate tra loro.
Le condizioni necessarie di stabilità assoluta si ottengono imponendo la stabilità globale dello stato nullo per una classe di funzioni φ più ristretta di Φ[k1, k2], in particolare si fa riferimento alle funzioni lineari:
In questo modo il sistema non lineare si riduce ad un sistema lineare con k che sostituisce l'elemento non lineare N. Per il nuovo sistema la stabilità globale dello stato di equilibrio corrisponde all'asintotica stabilità dell'intero sistema.
Per poter enunciarne la definizione è necessario dapprima introdurre la nozione di segmento ρ[k1, k2] come l'insieme dei numeri reali -1/k con k1≤k≤k2 e k≠0, poiché se k1=0 oppure k2=0 il segmento diventa una semiretta oppure se k1<0 e k2>0 il segmento degenera in due semirette. Detto questo, è possibile definire
DEF 2: Condizione necessaria affinché il sistema canonico - inizio della trattazione - sia assolutamente stabile nel settore [k1, k2] è che il numero di giri percorsi in senso antiorario dal diagramma di Nyquist di Γ(s) attorno al segmento ρ[k1, k2] sia ben definito e risulti pari al numero di poli a parte reale positiva di Γ(s).
Determinare condizioni sufficienti di stabilità assoluta è molto difficile a causa delle non linearità. Infatti, non è possibile ricondurre lo studio di sistemi non lineari a quello di alcun sistema lineare. Per meglio comprendere il problema, nel seguito si riporta il criterio del cerchio (una estensione della parte sufficiente del criterio di Nyquist).
Occorre partire dalla nozione di cerchio σ[k1, k2], definita come la regione del piano complesso che contiene il segmento ρ[k1, k2] delimitata dalla circonferenza che ha centro sull'asse reale e passa per i punti -1/k1 e -1/k2. Si noti che se ρ[k1, k2] è una semiretta, σ[k1, k2] sarà un semipiano mentre ρ[k1, k2] è costituito da due semirette, σ[k1, k2] sarà l'intero piano complesso con l'esclusione dei punti interni alla circonferenza che delimitano la regione.
Condizione sufficiente affinché il sistema canonico sia assolutamente stabile nel settore [k1, k2] è che il numero di giri percorsi in senso antiorario dal diagramma di Nyquist di Γ(s) attorno al cerchio σ[k1, k2] sia ben definito e risulti uguale al numero di poli a parte reale positiva di Γ(s). La presenza di un'intersezione tra il diagramma polare di Γ(jω) ed il cerchio σ[k1, k2] non consente di dire nulla riguardo l'esistenza di stabilità assoluta, assumendo ovviamente che la condizione necessaria di cui sopra sia rispettata.
Funzione descrittiva
Si supponga che l'elemento non lineare N sia sollecitato da un ingresso sinusoidale
con E e ω reali e positivi.
Si consideri l'uscita periodica di periodo T=2π/ω, se il sistema è descritto dalla relazione ξ(t)=φ(ε) allora l'uscita periodica esiste ed è data da
Al contrario, se la caratteristica di N è a più valori, servendosi del medesimo ingresso le uscite saranno multiple; si supponga, allora, che tra queste ve ne sia sola una, periodica per alcuni valori di E. Si escludano i casi in cui le uscite siano periodiche costanti, in quanto si tratta di casi privi di interesse. Se l'uscita del blocco è non lineare, si può sviluppare la corrispondente serie di Fourier (qualcosa sulla trasformata e la serie è presente in un precedente articolo) e quindi scrivere:
Si prendano solo gli n dispari dello sviluppo in serie in quanto l'elemento non lineare N ha una simmetria dispari. Inoltre, la sua non linearità è di tipo algebrico (non dinamico), vuol dire che l'uscita dell'elemento non lineare non dipende dalla pulsazione dell'ingresso che l'ha generata ma è determinata univocamente dalla relativa caratteristica statica (ovvero la non linearità non è descritta da un'equazione differenziale).
Quanto appena esposto traspare nella precedente relazione guardando il coefficiente della serie di Fourier che non dipende dalla pulsazione dell'ingresso ma solo dall'ampiezza E. Se N è una funzione ad un solo valore, i coefficienti Ξ2n+1 sono reali perché φ(E cos(ωt)) è una funzione pari. Quindi, è possibile definire la funzione descrittiva N come:
La funzione descrive l'elemento non lineare per calcolare la prima armonica della sua uscita periodica generata dall'ingresso cosinusoidale. Estende, in questo caso, il concetto di risposta in frequenza di un sistema lineare stazionario. In generale la funzione descrittiva è complessa:
Il metodo
Si assuma che ξ(t) possieda il seguente sviluppo in serie di Fourier:
Se la funzione di trasferimento del processo Γ(s) non ha poli nell'origine, l'uscita χ(t) del sistema canonico avrà la seguente forma:
Se è rispettata la seguente relazione:
allora l'uscita del sistema canonico χ(t) sarà costituita, approssimativamente, dalla prima armonica. La condizione appena espressa rappresenta l'ipotesi dell'azione filtrante, non verificabile in maniera diretta sulle equazioni del problema ma, se non verificata, il metodo della funzione descrittiva perde di significato.
Una giustificazione dell'ipotesi dell'azione filtrante è data dalle seguenti condizioni:
- L'ampiezza delle armoniche di ordine superiore al primo è di solito molto minore di quella fondamentale
- La parte lineare del sistema Γ(s) in genere si comporta come un filtro passa-basso, pertanto si riduce l'ampiezza delle armoniche di ordine superiore al primo.
Quanto detto finora rende il metodo della funzione descrittiva un metodo euristico. La condizione dell'ipotesi dell'azione filtrante non vuol dire supporre che il movimento periodico di ξ sia puramente sinusoidale, ma vuole mettere in evidenza che se Γ(jω) è di tipo passa-basso, allora il movimento dell'uscita del sistema canonico χ(t) è approssimativamente sinusoidale. La condizione dell'azione filtrante deve essere soddisfatta in maniera congiunta da Γ(s) e ξ(t).
Se l'azione filtrante vale al limite, si ottiene:
Data la libertà nel posizionare l'origine dell'asse temporale, lo si può porre in modo tale da rendere vero che:
Allora ε(t) avrà la forma
L'ipotesi di azione filtrante implica che l'ingresso del blocco non lineare N sia una sinusoide, affinché esso possa essere descritto dalla funzione descrittiva. Perché l'oscillazione sia compatibile con il sistema canonico, deve rispettare tutte le condizioni dettate dagli elementi che costituiscono quest'ultimo, quindi si ricava:
Con la condizione:
Deve risultare:
Quindi se Γ(s) non ha poli a parte reale nulla, data l'ipotesi dell'azione filtrante, allora il sistema canonico ammette un'oscillazione avente forma:
Sotto l'ipotesi in cui E (segnato) ed ω (segnato) sono soluzioni dell'equazione di cui sopra. Questa è detta equazione pseudocaratteristica per via della sua somiglianza con l'equazione caratteristica di un sistema retroazionato lineare. La quantità Γ(ω)D(E) sostituisce la risposta in frequenza d'anello che è estesa a funzioni non lineari tramite la funzione descrittiva.
Si è interessati al caso in cui D(E)≠0, per cui si può porre:
E si ottiene:
Ci si rende conto del fatto che ogni soluzione data dalla coppia (E, ω) di quest'ultima relazione, corrisponde ad un'intersezione tra il diagramma polare di Γ(jω), al variare di ω, e la rappresentazione nel piano complesso Λ(E) al variare di E, dove E rappresenta l'ampiezza dell'ingresso puramente sinusoidale ed ω la sua pulsazione. La rappresentazione nel piano complesso di Λ(E) prende il nome di luogo dei punti critici. Ci si attende che i diagrammi di Γ(jω) e di Λ(E) continuino ad intersecarsi anche in presenza di piccole perturbazioni dei sistemi.
Per definire la stabilità dei sistemi canonici che ammettono oscillazioni permanenti ci si riferisce ad una tecnica euristica, rimanendo nell'ambito della funzione descrittiva. Supponendo che il sistema ammetta oscillazioni per la coppia (E, ω), che è soluzione dell'equazione pseudocaratteristica, la sua risposta è detta asintoticamente stabile in presenza di movimenti di ε che differiscono di poco dal movimento nominale e tendono a coincidere con esso in maniera asintotica (ammettendo uno sfasamento temporale).
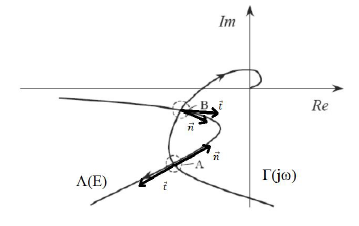
Si definiscono due vettori: t, tangente al diagramma dei punti critici di Λ(E) e orientato nel verso delle E crescenti; n, normale al diagramma polare di Γ(jω) ed orientato verso destra percorrendo il suddetto diagramma nel verso delle ω crescenti. Pertanto l'oscillazione di equazione ε(t)= E cos(ωt) è asintoticamente stabile se e solo se il prodotto scalare tra i vettori t ed n è negativo:![]()
Quindi la stabilità dipende dal fatto che i due vettori t ed n formino o meno un angolo di 90°. Questo metodo, in quanto euristico, è soggetto ad errori in casi critici. In Figura 2 si vedono due intersezioni tra il diagramma polare di Γ(jω) ed il luogo dei punti critici di Λ(E) corrispondenti a due possibili soluzioni del problema, quindi due possibili coppie (EA, ωA) ed (EB, ωB).
Applicando la definizione di stabilità appena enunciata, si può notare che solo l'oscillazione corrispondente al punto A è asintoticamente stabile poiché l'angolo formato dai due vettori è maggiore di 90°.
Invertitore CMOS
L'invertitore è un dispositivo molto importante in quanto è il nucleo di tutti i sistemi digitali, pertanto, analizzando il suo comportamento, si riesce facilmente a studiare e progettare circuiti digitali più complessi. Di seguito sono mostrate le proprietà statiche e dinamiche dell'invertitore CMOS (una particolare implementazione dell'invertitore).
In un nostro precedente articolo potrete trovare anche una breve sintesi delle differenze che intercorrono tra i CCD ed i CMOS.
Comportamento statico
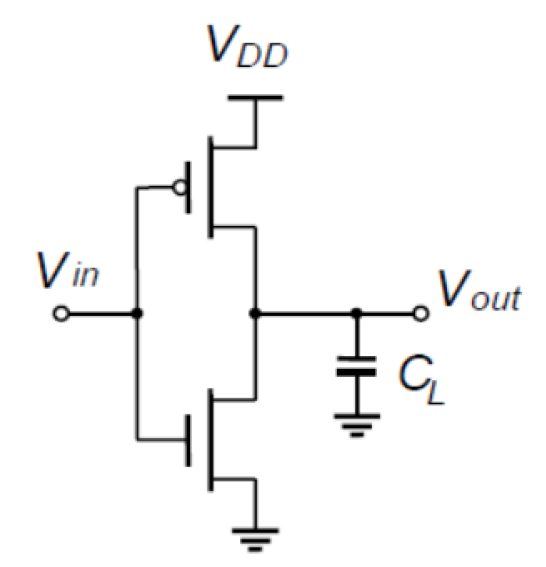
Lo schema circuitale dell'invertitore CMOS è mostrato in Figura 3:
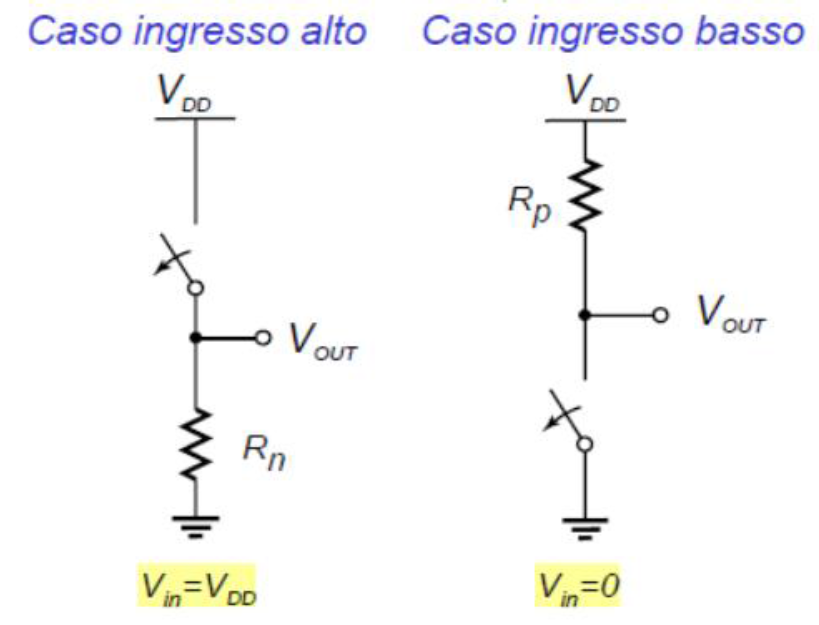
Per analizzarne il comportamento statico si usa, in prima approssimazione, il modello dell'interruttore del transistor NMOS (o PMOS). Il transistor può essere visto come un interruttore con una resistenza infinita quando è aperto (si avrà |VGS|<|VT|) ed una resistenza finita quando è chiuso (|VGS|>|VT|).
Se in ingresso all'invertitore si ha il valore logico alto (VDD), l'NMOS sarà in conduzione mentre il PMOS sarà interdetto, pertanto in uscita si avrà il livello logico basso. Al contrario, se in ingresso si ha il valore logico basso (0V), l'NMOS sarà interdetto ed il PMOS sarà in conduzione, quindi all'uscita si avrà il valore logico alto (VDD). Quindi questo circuito realizza la funzione logica NOT.
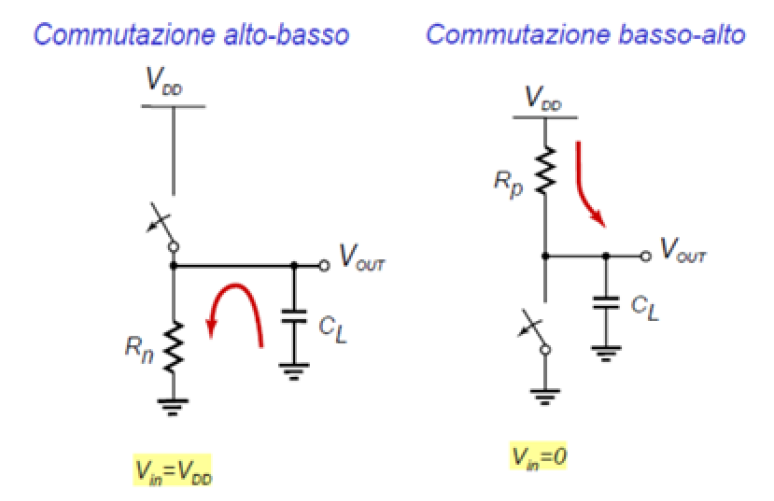
In condizioni stazionarie, a regime esiste sempre un cammino diretto tra uscita e massa come mostrato in Figura 4:
Come accennato in precedenza, i valori logici alto e basso corrispondono alla tensione di alimentazione (VDD) e 0V. Questa proprietà contraddistingue le porte logiche dette "non a rapporto", cioè quei dispositivi i cui livelli logici non dipendono dal rapporto delle dimensioni dei transistor che li compongono. Le porte logiche "a rapporto" invece, sono chiamate così perché i valori logici dipendono dal rapporto delle dimensioni dei transistor.
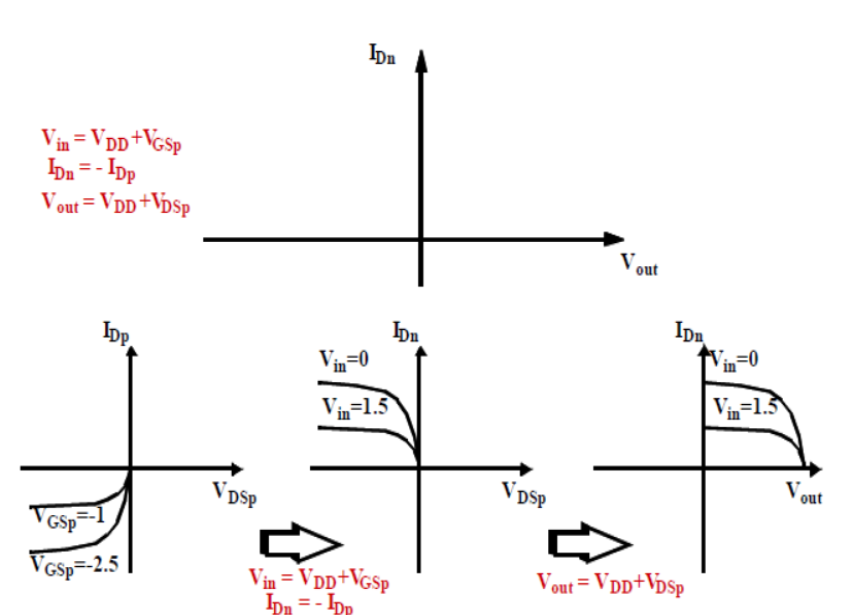
La caratteristica ingresso uscita del CMOS può essere ricavata graficamente tramite il metodo della curva di carico, cioè tracciando le curve corrente-tensione dell'NMOS e del PMOS sullo stesso grafico. Per farlo si rappresentano, nello stesso sistema di coordinate, le correnti di drain dei due transistor per poi traslare nel nuovo sistema di riferimento la caratteristica corrente - tensione del PMOS attraverso le seguenti relazioni:
In questo modo si ottiene la curva di carico del PMOS invertita rispetto all'asse x e traslata verso destra di VDD, come esposto in Figura 5:
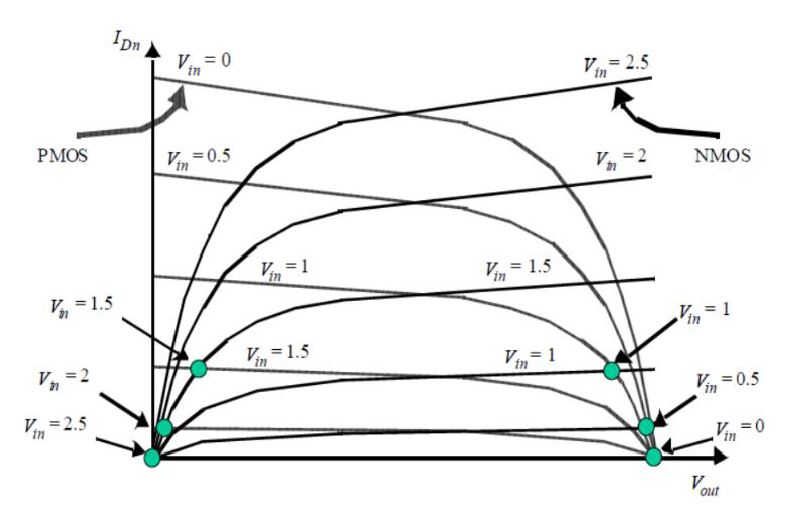
Nei grafici in Figura 5 si è assunto VDD=2.5V e |Vt|=0.5V. Sovrapponendo le curve di carico dell'NMOS si ottiene il grafico di Figura 6.
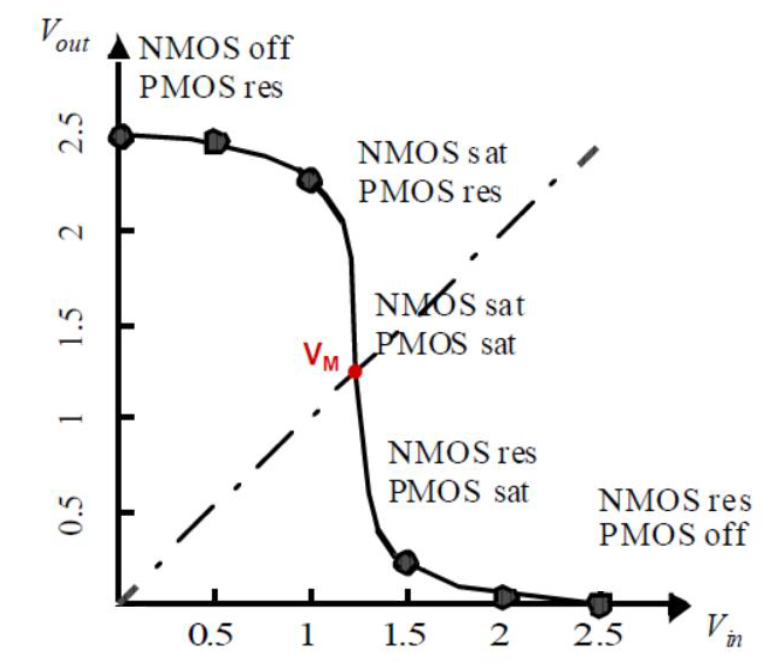
Per avere un valido punto di lavoro le correnti dei due dispositivi devono essere uguali, guardando il grafico (Figura 5) questo vuol dire che il punto operativo deve trovarsi in corrispondenza dell'intersezione delle curve di carico del PMOS e dell'NMOS. Si osserva che tutti questi punti di intersezione si trovano o in corrispondenza del valore logico alto o del valore logico basso. Quindi si deduce che la caratteristica di trasferimento ingresso-uscita dell'invertitore ha una regione di transizione molto stretta, tale effetto è dovuto all'elevato guadagno del circuito che si presenta quando entrambi i transistor sono accesi in saturazione. In presenza di un punto di lavoro nella regione, una piccola variazione dell'ingresso provocherà un'ampia variazione dell'uscita. Pertanto si otterrà la caratteristica ingresso-uscita del CMOS mostrata in Figura 7.
Comportamento dinamico
Operando un'analisi qualitativa del comportamento dinamico di un invertitore CMOS si ha che la risposta dinamica è principalmente dominata dalla capacità CL vista tra l'uscita della porta e la massa. Si compone di vari contributi capacitivi parassiti:
- capacità parassite di drain dei due transistor
- capacità di gate-drain
- capacità delle piste di interconnessione
- capacità di ingresso, di eventuali porte logiche che l'invertitore pilota
Supponendo che l'ingresso commuti istantaneamente.
Guardando ancora una volta il modello ad interruttori dell'invertitore si può avere un'idea del suo transitorio.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3940 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.


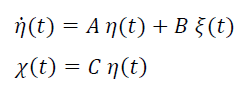
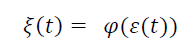
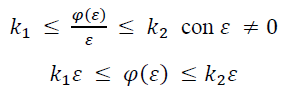
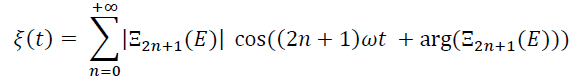

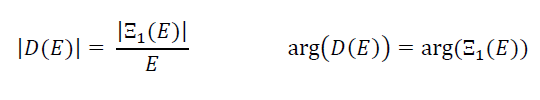

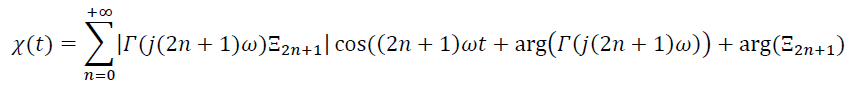
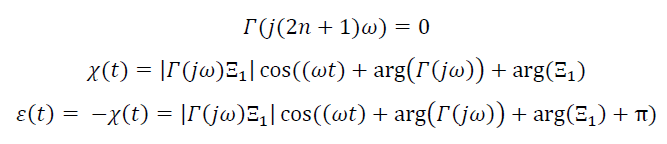
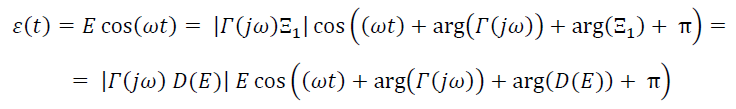

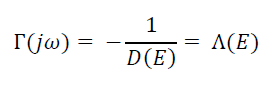
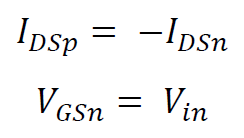
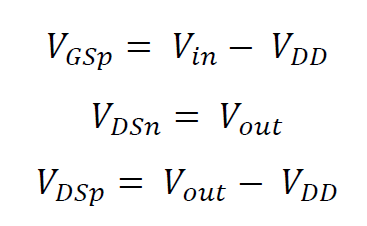






Un articolo che dimostra chiaramente come i concetti di matematica avanzata, per quanto complessi, da spiegare e ovviamente da comprendere, siano ben radicati nella nostra vita di tutti i giorni, dato che, come accade in questo caso, le applicazioni riguardano componenti fondamentali per tutti gli odierni circuiti elettronici, compresi quelli che costituiscono l’hardware dei nostri smartphone ad esempio.