Nell'articolo saranno esaminati alcuni metodi per il calcolo di questa importante funzione, seguiti anche da numerosi esempi pratici per comprenderne a fondo il funzionamento, in modo da effettuarne successivamente la relativa implementazione nel sistema. Sarà data molta importanza alla possibilità di realizzazione di algoritmi per l'utilizzo meccanizzato delle procedure su elaboratori elettronici.
Con la tecnologia attuale, il calcolo del logaritmo di un numero è cosa semplice. Basta disporre di una calcolatrice scientifica o di un computer, ed il gioco è fatto. Qualche decennio fa si utilizzavano le tavole logaritmiche, che consistevano in una successione molto grande di dati precalcolati, con cui era anche semplice calcolare il logaritmo di un numero. Eppure ci sono dei casi in cui si deve effettuare il calcolo del logaritmo senza effettivamente disporre della sua funzione diretta, ossia occorre calcolarlo "a mano" con l’ausilio delle quattro operazioni fondamentali, più qualcuna aggiuntiva, come l’elevamento a potenza o la radice quadrata. Questo avviene, ad esempio, se si deve implementare la funzione in un sistema sprovvisto di calcolo del logaritmo diretto, come ad esempio un linguaggio di programmazione semplice, oppure in un sistema embedded o a microcontrollore.
Metodo diretto
Il metodo più semplice ed immediato è quello di utilizzare le funzioni appropriate nelle calcolatrici e nei linguaggi di programmazione. La maggior parte dei sistemi mettono a disposizione le funzioni per il rapido calcolo, soprattutto in base 10 e in base E. Con le equazioni riportate nella nomenclatura è tuttavia possibile calcolare il logaritmo in qualsiasi base, con una semplice divisione.
Formula di Borchardt
Si tratta di una elegante e comoda formula, per lo più immediata, utile quando i valori su cui trovare il logaritmo naturale sono bassi. La funzione è infatti abbastanza precisa per valori di x fino a 20, ma essa comincia a divergere e a perdere significato utile, quando le quantità cominciano a salire. La formula è la seguente:
Si può implementare su qualsiasi linguaggio di programmazione poiché, come si osserva, essa prevede solo la sottrazione, l’addizione, la divisione, la moltiplicazione e l’elevamento a potenza. Occorre però, come detto, utilizzare piccoli valori noti.
Espansione delle Serie
Molte funzioni reali, tra cui quella del logaritmo naturale, sono sviluppabili attraverso le serie di Mac Laurin. In questa trattazione interessa solamente quella per calcolare il logaritmo neperiano di un qualunque numero. L’unico problema dell’espansione delle serie, specialmente di questo tipo, è dato dalla lentezza intrinseca del metodo, in quanto essa converge molto lentamente e, per alcuni casi, vengono coinvolti risultati parziali molto grandi. Inoltre il dominio di convergenza risulta alquanto limitato.
Metodo di avvicinamento
Questo metodo si attua tramite un algoritmo. La sua filosofia sta nel rintracciare il valore del logaritmo di un numero mediante avvicinamento. Normalmente, il valore simulato parte da zero e incrementa di uno specifico passo, fino a raggiungere il risultato. Più piccolo è il passo e più preciso risulterà il risultato finale, anche se occorrerà maggiore tempo per la sua conclusione. Di seguito è mostrato il listato di programma, scritto in linguaggio C, che offre una velocità maggiore di ogni altro linguaggio:
#include <stdio.h>
#include <math.h>
void main() {
float n,logaritmo,base,elevazione;
n=98765;
logaritmo=0;
base=10;
while (1) {
elevazione=pow(base,logaritmo);
if(elevazione>n)
break;
logaritmo+=0.001;
}
printf("Il logaritmo e' %f\n",logaritmo);
}
Se occorrono valori diversi per l’operando o per la base, basta semplicemente modificare rispettivamente i valori della variabile "n" e "base".
Metodo dicotomico
Anche questo metodo si risolve tramite un algoritmo. Il tempo di ricerca è sicuramente inferiore a quello precedente, in quanto il valore del logaritmo è cercato con una strategia più intelligente. In pratica, il rintracciamento del valore non avviene sequenzialmente. Vengono invece posti due limiti (uno inferiore e uno superiore, inizialmente impostati a valori estremi) ed il risultato viene cercato nel punto centrale tra essi, ossia nella media aritmetica dei due limiti. I due limiti si avvicinano sino a trovare il risultato, a seconda che il calcolo di verifica sia maggiore o minore di quello cercato. Di seguito è mostrato il listato di programma, scritto in linguaggio C, che offre una velocità maggiore di ogni altro linguaggio:
#include <stdio.h>
#include <math.h>
void main() {
float n,minimo,massimo;
float base,mezzo,tentativo;
n=1234567;
minimo=0;
massimo=n;
base=10;
while (1) {
mezzo=(minimo+massimo)/2;
tentativo=pow(base,mezzo);
if(tentativo>n)
massimo=mezzo;
if(tentativo<n)
minimo=mezzo;
printf("Il logaritmo e' %f\n",mezzo);
}
}
Impostato in questo modo, il programma non termina mai, ma visualizza, passo dopo passo, il valore del logaritmo che si va avvicinando a quello reale, ad ogni iterazione del programma.
Metodo formula inversa
Per la risoluzione a formula inversa, è necessario risolvere il sistema seguente:
Metodo delle elevazioni
Si tratta di un metodo semplice e geniale che può essere eseguito anche tramite una calcolatrice non molto sofisticata e che può essere implementato in un algoritmo per qualunque linguaggio di programmazione, sprovvisto della funzione per il calcolo del logaritmo. Per attuare il metodo è sufficiente eseguire alcune elevazioni e alcuni conteggi.
Con un esempio pratico viene spiegato il metodo. Si debba calcolare il logaritmo di 150 in base 10.
Si divida 150 per 10 fino a quando il risultato è maggiore di 10. Si totalizzino quindi il numero delle divisioni. Il conteggio costituirà la parte intera del risultato.
150 : 10 = 15 (1°)
15 : 10 = 1,5 (2°)
Non potendo effettuare più divisioni, il risultato intero sarà 2, ossia il numero di divisioni. Adesso si possono calcolare le cifre decimali, con una precisione pressoché infinita.
Si proceda in questo modo: si elevi a 10 il risultato finale (1,5) e si proceda a dividere per 10 fino a quando la divisione lo consenta. Allo stesso modo si totalizzino il numero di divisioni. Tale risultato costituirà la prima cifra decimale:
1,5^ 10 = 57,66503906
57,66503906 : 10 = 5,766503906 (1°)
Non potendo effettuare più divisioni, la prima cifra decimale sarà 1, ossia il numero di divisioni.
Adesso si può calcolare la seconda cifra decimale. Si proceda in questo modo: si elevi a 10 il risultato finale (5,766503906) e si proceda a dividere per 10 fino a quando la divisione lo consenta. Allo stesso modo si totalizzino il numero di divisioni. Tale risultato costituirà la seconda cifra decimale:
5,766503906 ^ 10 = 40656117,75
40656117,75 : 10 = 4065611,775 (1°)
4065611,775 : 10 = 406561,1775 (2°)
406561,1775 : 10 = 40656,11775 (3°)
40656,11775 : 10 = 4065,611775 (4°)
4065,611775 : 10 = 406,5611775 (5°)
406,5611775 : 10 = 40,65611775 (6°)
40,65611775 : 10 = 4,065611775 (7°)
Procedendo in questo modo si possono calcolare tante cifre decimali, con una normale calcolatrice. Raccogliendo il numero di divisioni effettuate il risultato è il seguente:
LOG(150)=2,17…….
Si spera che questa piccola raccolta contribuisca allo studio e all’approfondimento dei metodi e degli algoritmi per il calcolo dei logaritmi.
Si invitano i lettori a porre domande, suggerimenti o a fornire, eventualmente, altri metodi noti o meno, per il calcolo del logaritmo.

Ti potrebbe interessare anche:

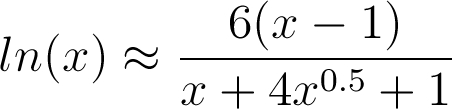
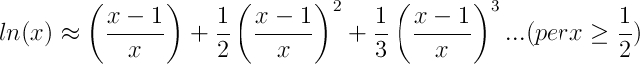
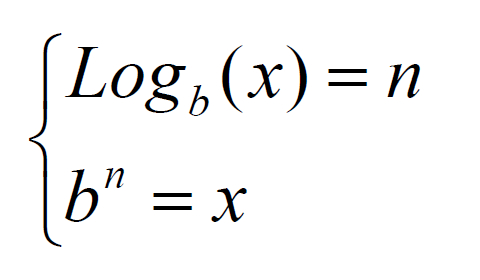







Resto sempre affascinato da quanto, nella matematica, tutto quadri alla perfezione.
Esiste una strada (se non di più) per arrivare ad ogni risultato ed ognuna di esse è più o meno interessante/tortuosa/elaborata.
Parafrasando Galileo Galilei, la matematica è davvero il linguaggio di Dio.
Purtroppo non conosco altri metodi ma avrei volentieri contribuito a completare questa raccolta.
Non potrei essere più d’accordo di così 🙂
Non mi vengono in mente altri metodi ma ho modificato leggermente il tuo programma per fare risolvere al programma tutti i logaritmi che voglio senza fissarlo dall’interno al numero n da te scelto.
#include <stdio.h>
#include <math.h>
#include <conio.h>
int main() {
float n,logaritmo,base,elevazione;
printf(“Inserisci n\t”);
scanf(“%f”,&n);
// n=98765;
logaritmo=0;
base=10;
while (1) {
elevazione=pow(base,logaritmo);
if(elevazione>n)
break;
logaritmo+=0.001;
}
printf(“Il logaritmo e’ %f\n”,logaritmo);
getch();
}</conio.h></math.h></stdio.h>