
Parlando di crittografia, ci sono due sistemi di autenticazione: un primo metodo "simmetrico", che fa affidamento a chiavi condivise tra l'host e chi deve autenticare, ed uno "asimmetrico", che si basa su un gioco tra chiavi pubbliche e private condivise sfruttando il sistema di riconoscimento ECDSA (Elliptic Curve Digital Signature Algorithm). In sistemi aperti, nei quali parti terze hanno la necessità di autenticarsi, la gestione e la protezione delle chiavi di accesso è un argomento molto delicato. Proprio in questo contesto il sistema "asimmetrico" assicura una maggior flessibilità attraverso un sistema di gestione delle chiavi di sicurezza (pubbliche e private), sfruttando il principio della Crittografia a Curva Ellittica. L'uso della crittografia ECDSA a chiave pubblica riduce notevolmente i costi dei sistemi e nello stesso tempo la complessità digitale della conservazione delle chiavi.
Introduzione
Tipicamente l'autenticazione dei sistemi richiede l'uso di algoritmi simmetrici (come per esempio "l'algoritmo di hash") che richiedono una chiave segreta. Ad oggi, però, la gestione e la protezione di queste chiavi sta cambiando e si sta sempre più puntando su sistemi che usano una logica basata sulla curva crittografica ellittica o ECC (Elliptic Curve Cryptography). Con questa tecnica tutti i dispositivi connessi usano una coppia di chiavi, una privata ed una pubblica, aventi caratteristiche diverse: quella privata è usata per generare un messaggio mentre quella pubblica è usata per verificarne l'autenticità.
Curva ellittica
L'ellisse, in matematica, è definita dall'equazione di secondo grado in x e y con coefficienti che esprimono la forma della curva nel piano cartesiano. La curva ellittica crittografica, invece, usa un'equazione di terzo grado. Esistono due tipi di curve ellittiche crittografiche per quanto riguarda l'ECC: una pseudo-casuale, i cui coefficienti sono generati da una funzione di hash, e altri tipi di curve, dove i coefficienti sono scelti opportunamente per ottimizzarne l'efficienza. Le curve pseudo casuali possono essere definite al di sopra del campo finito GF(p) e del campo binario GF(2m). Il campo finito GF(p) contiene al suo interno un numero p di elementi, che sono integrati modulo p. La curva ellittica, in questo caso, ha la seguente equazione:
Il campo binario GF(2m), invece, è un tipo di campo che contiene 2m elementi, che rappresentano il numero di bit della stringa di lunghezza m. La curva ellittica, in questo caso, ha la seguente equazione:
Tuttavia ci sono un numero illimitato di possibili curve che possono soddisfare l'equazione ma solo un piccolo numero è significativo per questo tipo di crittografia. Ognuna è definita dal nome e dall'insieme dei suoi parametri (come per esempio il modulo primo p, il primo ordine n, i coefficienti a e b e le coordinate G(x,y) della curva).
Generazione delle chiavi
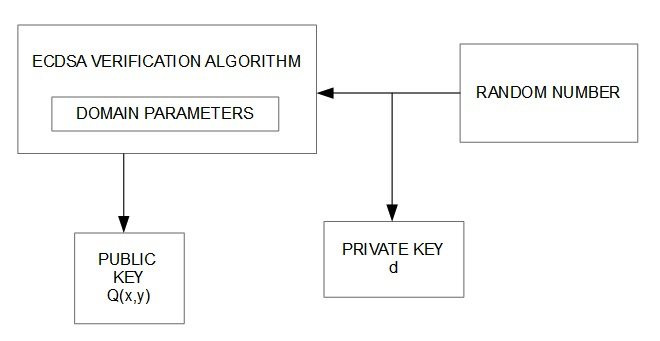
Prima che un sistema, con autenticazione tramite ECDSA, possa funzionare è necessario che si conosca la sua chiave privata; la chiave pubblica, infatti, deriva direttamente dall'unione di quella privata e da alcuni parametri. Entrambe le chiavi sono contenute nella memoria del sistema di autenticazione e, come è facilmente intuibile dai nomi, quella privata non è accessibile dall'esterno mentre quella pubblica, in contrasto, può essere letta liberamente da tutti. In Figura 1 è mostrato il processo di generazione per entrambe le chiavi.
Per prima cosa viene generato un numero casuale che, una volta finito il suo compito, trasmette il valore numerico ad un altro sistema atto a generare la chiave pubblica. Questo numero casuale diventa il valore della chiave privata, ed è un numero scalare d. Quindi viene [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2114 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.


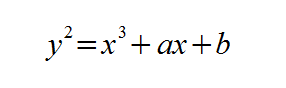
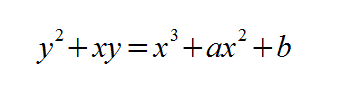






La crittografia ECDSA permette di ridurre i costi di gestione delle chiavi rispetto ad altre soluzioni, trovando di fatto spazio nei sistemi embedded. Può esprimere il senso della matematica che viene in aiuto nell’elettronica, mettendo a disposizione una scelta decisamente efficace per la protezione dei dati.