a L.C. colei che riempie i miei pensieri senza una logica

Il matematico George Boole, nella sua opera “L'Analisi matematica della logica”(1847) e quella divulgativa “Le leggi del pensiero” (1854) raggiunse due importanti risultati: da un lato, si realizzava il sogno di Raimondo Lullo (Ars Magna,1274 ) e Leibniz (Ars Combinatoria,1666) di ridurre il ragionamento al calcolo, dall'altro, in un solo colpo si scopriva che la logica proposizionale di Crisippo e quella sillogistica di Aristotele erano due aspetti della stessa realtà. La logica classica veniva così ridotta ad un semplice calcolo di sottrazioni, addizioni e moltiplicazioni e riprendendo il gioco dei numeri binari bastava sostituire il vero con 1 ed il falso con 0.

Porte Logiche

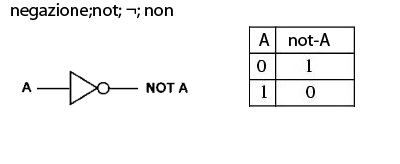
La negazione di una proposizione  la si poteva  considerare come una sottrazione  (1-1=0 , 1-0=1) e se le scelte ammissibili erano solo due la negazione non può far altro che trasformare il vero in falso e viceversa ed una doppia negazione in una affermazione (¬ ¬p= p).
In elettronica la negazione è rappresentabile con la porta  Not, in logica   con il simbolo ¬  e nel linguaggio naturale con l'espressione  non.

La disgiunzione inclusiva diventa una  semplice somma e la disgiunzione  di due proposizioni p o q  risultava falsa solo se entrambe sono false (0+0=0)  , vera se almeno una delle due preposizioni è vera (1+0=1;0+1=1;1+1=1). Invece la disgiunzione esclusiva è vera solo se uno dei disgiunti è vero , (1+0=1;0+1=1) dunque escludendo che lo siano entrambi  (0+0=0; 1+1=0).
Crisippo amava raccontare che persino il suo cane lo intuisse, tanto che quando rincorreva una lepre e giungeva a un bivio, sapeva  quale strada la preda avesse imboccato semplicemente annusando il primo sentiero e, se non ne sentiva l'odore , si lanciava sull'altro sentiero, senza bisogno di annusarlo.
In elettronica la disgiunzione  inclusiva diviene la porta Or , quella esclusiva Xor ,  in logica si usa prettamente il simbolo inclusivo ∨ .
Nel linguaggio naturale la disgiunzione, a seconda del senso o del contesto della proposizione, può  acquisire due significati distinti: l'inclusivo  vel latino  , da cui il simbolo ∨,  ad esempio: “Emanuele ascolta la radio o guarda la televisione” ed uno esclusivo aut: “Emanuele o ascolta la radio o guarda la televisione”.

Infine la congiunzione   diventa una semplice moltiplicazione e la congiunzione di due proposizioni p e q (es:piove e fa freddo) era vera solo se entrambe erano vere (1x1=1) invece falsa se una delle due era vera (1x0=0, 0x1=0, 0x0=0).
Congiunzione rappresentabile in elettronica con la porta And, in logica con il simbolo ⋀    e nel linguaggio naturale  con e

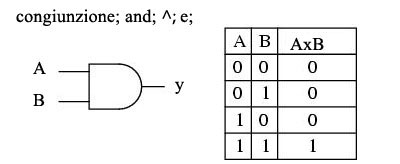
Infine riprendendo la tesi di Shannon la negazione  si poteva considerare come un interruttore in parallelo con la lampadina, la congiunzione come due interruttori disposti in serie e la disgiunzione si poteva infine considerare come due interruttori disposti in parallelo.

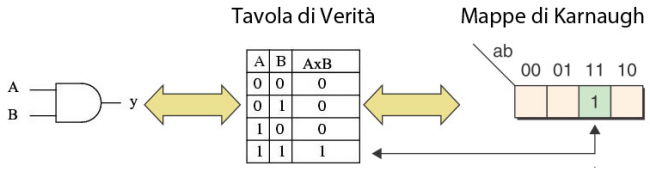
Tavole di Verità

Le definizioni sinora date possono essere tutte descritte attraverso le tavole di verità, che oltre a darci le matrici dei connettivi possono essere usate per il  calcolo logico.
Le tavole furono usate da Boole (1847) , Frege (1879) e Peirce (1880), ma divennero famose solo a partire dal 1921 con Ludwig Wittgenstein nel Tractatus logico-philosophicus (TLP).
Il rapporto che lega congiunzione e disgiunzione  si deve al matematico Augustus De Morgan (Logica Formale,1847) che scoprì che   la tavola di verità di  p ⋀ q è uguale  a ¬ ( ¬ p ∨  q ¬) e  che quella di  p ∨ q a ¬ ( ¬ p ⋀  ¬q ).
Leggi già note allo scolastico Guglielmo di Ockham nella “Summa Logicae” e da Walter Burleigh nel “De Puritate”.

Le tavole di verità però sono solo uno dei tanti tentativi   di risolvere meccanicamente questioni logiche mediante  figure geometriche, ad esempio nell'antichità troviamo l'utilizzo  di cerchi o ellissi  per visualizzare i sillogismi aristotelici.
Nel 1686 Leibniz , nelle “Difficultates Quaedam Logicae”,  fu il primo ad accorgersi attraverso i cerchi che la logica sillogistica non era altro che un semplice calcolo sugli insiemi. Il passo successivo lo fece Boole interpretando la sottrazione come gli elementi che non fanno parte di A, la somma come l'unione degli elementi che fanno parte di A o B  ed invece il prodotto come l'intersezione di A e B.
La rappresentazione di Leibniz venne ripresa nel 1761 dai diagrammi del matematico Eulero nelle “Lettere a una principessa tedesca” , nel 1881 da John Venn ed infine nel 1896 da Lewis Carroll  in due opere dal medesimo titolo “Logica Simbolica”.
Invece i primi diagrammi basati su quadrati o rettangoli vennero introdotti nel 1881 dal filosofo Allan Marquand e riprese nel 1953  dall'ingegnere Maurice Karnaugh.

I tre principi aristotelici

George Boole ebbe il merito di trasformare  la logica in algebra non andando però al di là   di  Aristotele da cui  ne eredita i tre  principi. Nella logica classica possiamo esprimere nel seguente modo il principio d'identità: p → p  secondo cui ogni cosa è uguale a se stessa.
Il principio di non contraddizione  “è il più fermo di tutti i principi” perché “è impossibile per lo stesso attributo appartenere o non appartenere allo stesso soggetto dallo stesso punto di vista”. (Metafisica, libro IV,Aristotele).
Una stessa formula non può quindi essere sia vera sia falsa e possiamo scriverlo così ¬(p ⋀  ¬p) e nella forma sillogistica significa  che allo stesso tempo niente può stare dentro e fuori da un cerchio.
In occidente questo principio caratterizzerà  la logica dell'essere di Parmenide e di Aristotele contrapponendosi a quella del divenire di Eraclito e di Hegel.
Altro principio  è quello del terzo escluso  (p ∨ ¬ p) cioè “non è possibile che ci siano alternative a una contraddizione, ed è necessario affermarne una e negare l'altra”(Metafisica, libro IV,Aristotele). In forma sillogistica è rappresentabile  come una cosa può stare fuori o dentro di un cerchio.In sostanza  equivale al principio di bivalenza del  logico polacco  Jan Łukasiewicz cioè ” una proposizione può essere vera o falsa”.
Anche se questo comporta dei problemi per “i futuri contingenti” cioè nel domandarci se le proposizioni che esprimono fatti inerenti al futuro ,che possono quindi sia accadere che non, posseggano già nel presente un valore logico  determinato .
Problema che non era sfuggito nemmeno ad Aristotele che ne fa menzione nel nono capitolo dell'Interpretazione riferendosi se “Domani ci sarà una battaglia navale”, ma alla fine la questione si risolse dando ragione alla scuola stoica di Crisippo.
Gli atteggiamenti a favore o contro il principio di bivalenza rispecchiano  diverse visioni del libero arbitrio , ad esempio Epicuro,secondo una testimonianza di Cicerone (De Fato),  ne rifiutò la validità per salvaguardarlo invece gli stoici  essendo fatalisti lo accolsero e lo difesero senza remore .

Logica polivalente

Se la logica classica aveva assimilato il principio di non contraddizione  e del terzo escluso possiamo rintracciarne una loro negazione nella forma di “coincidenza degli opposti”  nella filosofia della religione in Niccolò Cusano (1401-1464), della storia in Friedrich Hegel (1770-1831) e politica in Karl Marx (1818-1883).
Invece in logica una delle prime alternative  fu proposta dal matematico olandese   Luitzen E. J. Brouwer (1881-1966) che  pubblicò “L'inaffidabilità dei principi logici” (1908) osservando che  se volessimo estendere la  validità della logica classica dal finito all'infinito  il principio del terzo escluso (p ∨ ¬ p) e della doppia negazione (¬ ¬p= p) sarebbero poco affidabili.
Una prima formulazione di logica polivalente però risale al 1920 da parte del matematico polacco Jan Łukasiewicz (1878-1956)  che propose  un terzo valore, oltre al vero ed al falso,  che tenesse conto di proposizioni circa “eventi contingenti” del tipo:”a Natale sarò a Varsavia ”.
Riprendendo l'argomentazione di Łukasiewicz: la proposizione considerata non è oggi né vera né falsa e deve possedere un terzo valore, diverso da “0” o falsità e da “1” o verità. Possiamo denotare questo valore con “1/2”. Esso è proprio “il possibile”, che si affianca al “vero” e al “falso” come terzo valore. [...]il sistema trivalente della logica proposizionale deve la sua origine a questa linea di pensiero.

Ridefinendo le tavole di verità otterremo che nella congiunzione considererò il più piccolo fra p e q ad esempio se p=1 e q=1/2  allora  p ⋀ q sarà uguale ad 1/2. Invece  il più grande nella disgiunzione fra  p e q così che se p=0 e q=1/2, allora il valore di  p ∨ q sarà 1/2.Inoltre volendo sostituire i valori con  1 e 0  notiamo che valgono le stesse regole della logica classica. La logica trivalente del matematico polacco non sarà altro che un anticipazione della logica Fuzzy del matematico iraniano Lofti Zadeh.
Da qui in poi continua Alessandra De Angelis con il suo articolo provocatorio  sul “Perché la logica Fuzzy è stato un fallimento” .

Bibliografia
B.Russell, Storia della filosofia occidentale,Tea,Milano, 2006
F.Berto, La logica da zero a Godel, LaTerza,Roma,2008
N. Kretzmann, La logica nel medioevo,Jaca Books, Milano,1999
Bobzien S., Determinism and freedom in Stoic philosophy, Oxford, Clarendon Press, 1998
B.Kosko, Il fuzzy-Pensiero,Baldini&Castoldi,Milano,1995
A.Pizzaleo, Logica Fuzzy, Castelvecchi,Roma,2004

Sitografia
A. De Angelis,Ludwig Wittgenstein: i computer parlano la nostra stessa lingua?, EOS, 2012
A. De Angelis,Perché la logica Fuzzy è stato un fallimento, EOS, 2012
L.Dori, Mappe di Karnaugh, EOS,2011

Andres Reyes

Integrational Mind Labs (Iml)
Coordinatore sezione Junior
http://integrationalmindlabs.it/
Come aderire:
http://integrationalmindlabs.it/iml-adesioni.html

Articoli Correlati

Perché la logica Fuzzy è stata un fallimento

Perchè il nostro cervello non può essere un computer?