Con questo articolo ho cercato di illustrare, nella maniera più chiara e sintetica possibile, i risultati di alcune ricerche finalizzate a minimizzare il consumo di propellente in una missione lunare. Tali studi hanno condotto alla scoperta di alcune traiettorie che sono, in un certo senso, delle "scorciatoie" che non fanno risparmiare tempo ma carburante ad un veicolo spaziale diretto verso la Luna.

Introduzione

Un veicolo spaziale, per modificare la sua traiettoria, deve eseguire quelle che si chiamano manovre impulsive o manovre orbitali, ossia deve azionare il proprio sistema di propulsione, il quale genera una spinta che modifica repentinamente la velocità del veicolo portandolo su una nuova traiettoria. Ad ogni manovra impulsiva corrisponde quindi una certa variazione di velocità, detta anche impulso, che è pari a

dove

e

sono le velocità del veicolo, rispettivamente, prima e dopo la manovra, all'interno di un sistema di riferimento cartesiano xyz concentrico e solidale con il corpo celeste che, col proprio campo gravitazionale, influenza maggiormente il suo moto.

Un esempio è la tecnica di Hohmann, che consente di effettuare il trasferimento di un satellite tra due orbite circolari complanari tramite un’orbita ellittica il cui perigeo si trovi sull’orbita di partenza e l’apogeo su quella di arrivo. Il trasferimento orbitale avviene in due fasi: dapprima viene incrementata la velocità del satellite, in modo che esso passi dall’orbita circolare iniziale a quella ellittica di trasferimento; in seguito, un secondo incremento di velocità viene fornito al satellite all’apogeo dell’orbita ellittica, in modo da circolarizzarla a quella quota, ottenendo così l’orbita circolare finale desiderata.

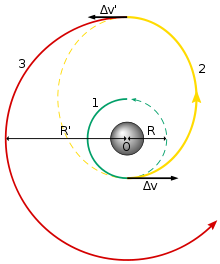
La somma dei ΔV associati alle varie manovre impulsive che il veicolo deve effettuare costituisce il ΔV totale necessario per poter compiere l'intero percorso previsto dalla missione spaziale. Noto quest’ultimo, la quantità di propellente di cui necessita il velivolo si ricava dall’equazione di Tsiolkovsky:

dove:

mp = massa del propellente;

m = massa del veicolo privo di propellente;

v = velocità (rispetto al veicolo) con la quale vengono espulsi i gas prodotti dalla combustione del propellente.

Un aspetto fondamentale della progettazione di qualsiasi missione spaziale è costituito dalla minimizzazione della quantità di propellente di cui deve essere dotato il velivolo, ovvero dalla minimizzazione del ΔV totale.

Le traiettorie di Sweetser e il calcolo del ΔV minimo

Nel 1991, il matematico Theodore H. Sweetser, ricercatore del Jet Propulsion Laboratory, calcolò il ΔV totale minimo teorico necessario per realizzare un trasferimento lunare. Il suo lavoro faceva parte della progettazione di una missione lunare della NASA che consisteva nel trasferire una sonda, chiamata Lunar Observer, da un’orbita circolare terrestre di 167 km di altitudine ad un’orbita circolare lunare di 100 km di altitudine.

Sweetser dimostrò che sarebbe occorso un impulso totale minimo pari a 3,721 km/s. La sua teoria, sviluppata approssimando il problema di un trasferimento Terra-Luna con il problema ristretto dei tre corpi (Terra, Luna, veicolo), è principalmente basata sull’analisi delle variazioni della costante di Jacobi, causate dalle manovre impulsive del veicolo spaziale (la formula che esprime questa costante è uno dei risultati ottenuti da Jacobi, nella prima metà del 19° secolo, studiando tale problema). Essa fornisce due condizioni necessarie affinché il ΔV totale di una missione lunare sia quello minimo teorico:

1. il veicolo deve transitare, con velocità rotazionale nulla, per il punto lagrangiano interno del sistema Terra-Luna;
2. le manovre devono essere eseguite nei punti in cui è massima la velocità rotazionale e in modo tale che l’impulso sia parallelo e concorde con essa.                                  

La teoria di Sweetser è illustrata dettagliatamente in un mio articolo che potete trovare a questo indirizzo.

Sweetser e i suoi collaboratori (S. M. Marsh, H. J. Pernicka e D. P. Scarberry) tentarono di individuare traiettorie lunari caratterizzate da un ΔV il più possibile prossimo a quello minimo teorico da egli calcolato. Utilizzando le due condizioni precitate, i 4 ricercatori hanno ottenuto, integrando numericamente le equazioni del moto del problema ristretto dei tre corpi, alcune traiettorie che richiedono un ΔV prossimo a quello minimo, anche se, purtroppo, esigono tempi di volo eccessivamente lunghi che le rendono poco convenienti ed, in particolare, assolutamente inadatte a missioni lunari con equipaggio.

La migliore traiettoria da essi trovata, progettata appositamente per un trasferimento identico a quello della sonda Lunar Observer, richiederebbe un ΔV totale pari a 3,823 km/s, 9 manovre impulsive e un tempo di volo di 292,02 giorni. È illustrata nei due grafici sottostanti; quello a sinistra rappresenta la traiettoria nel sistema sinodico e l’altro nel sistema siderale. Si può notare che essa è complanare al piano dell’orbita della Luna attorno alla Terra.

Il grafico a sinistra è raffigurato più chiaramente nella seguente immagine:

Pernicka e Scarberry, in seguito, perfezionarono il lavoro scoprendo che l’eccentricità dell’orbita lunare può essere sfruttata per ridurre i tempi di volo.

Questa tipologia di trasferimento lunare, inoltre, induce a prendere in considerazione la possibiltà di realizzare in futuro missioni lunari consistenti nel lanciare veicoli verso la Luna da una stazione spaziale collocata nel punto lagrangiano. In tal caso, occorrerebbe un impulso pari solamente a 0,1 m/s per spedire il veicolo verso la Luna. Inoltre, non ci sarebbe alcuna restrizione riguardante le finestre di lancio; in parole povere, ogni lancio potrebbe essere effettuato in qualsiasi momento.

Le traiettorie di Belbruno attraverso le Weak Stability Boundaries   

La teoria delle Weak Stability Boundaries (WSB) venne sviluppata nel 1986 da Edward Belbruno, ricercatore del Geometry Center nel Minnesota. Le WSB sono quelle regioni dello spazio interplanetario nelle quali gli effetti dei campi gravitazionali della Terra, del Sole e della Luna su un corpo di massa trascurabile, quale è un veicolo spaziale, tendono a bilanciarsi. In una tale condizione, è sufficiente un piccolo impulso impartito nella giusta direzione per fare in modo che il veicolo venga catturato dal campo gravitazionale del corpo celeste verso il quale lo si vuole inviare. Per questo motivo, secondo Belbruno ed il suo collega J. K. Miller, le WSB possono essere utilizzate per minimizzare il ΔV totale di una missione lunare.

Il trasferimento lunare ideato da Belbruno e Miller consiste nello spedire il veicolo direttamente verso la Luna, ma solo per fare in modo che riceva da essa un gravity assist che lo spinga verso una WSB posta a circa 1,5 milioni di km dalla Terra, dove l’attrazione gravitazionale solare tende a bilanciare quella del sistema Terra-Luna. All’interno della WSB va eseguita una piccola manovra impulsiva che consenta al velivolo di percorrere una traiettoria tale che venga catturato dal campo gravitazionale della Luna e inserito automaticamente in un’orbita lunare.

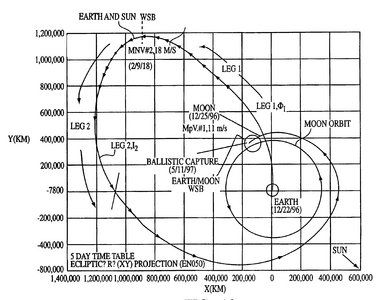
Traiettorie di questo tipo sono state calcolate da Belbruno e Miller integrando all’indietro nel tempo le equazioni del moto relative al problema ristretto dei 4 corpi (Terra, Sole, Luna, veicolo). Tale calcolo inizia determinando le condizioni che permettono la cattura del velivolo da parte del campo gravitazionale lunare; si prosegue poi attraverso l’integrazione all’indietro nel tempo fino al raggiungimento della Terra. Le uniche manovre richieste sono quella di iniezione dalla Terra e quella correttiva realizzata all’interno della WSB. Per questo motivo, il ΔV totale necessario per effettuare un trasferimento lunare utilizzando questo tipo di traiettoria è relativamente basso.

È stato calcolato che, per realizzare la missione del Lunar Observer usando la traiettoria di Belbruno e Miller, sarebbe occorso un impulso totale pari a 3,838 km/s, poco più del ΔV minimo calcolato da Sweetser.

Tale tecnica di trasferimento è stata applicata con successo alla sonda giapponese Hiten, che giunse in prossimità della Luna il 2 Ottobre del 1991.

Glossario  

Finestra di lancio - intervallo di tempo durante il quale un veicolo spaziale può essere lanciato. 

Gravity assist  o fionda gravitazionale  - tecnica di volo spaziale che utilizza il campo gravitazionale di un corpo celeste per modificare il percorso e la velocità del veicolo.

Problema degli n corpi  - studio del moto di n corpi soggetti unicamente alla loro mutua forza di attrazione gravitazionale. Si definisce ristretto  quando la massa e le dimensioni di uno di essi sono trascurabili rispetto a quelle degli altri.

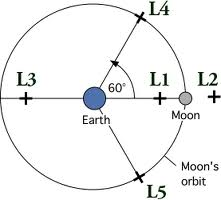
Punti lagrangiani  - punti dello spazio interplanetario dove le forze gravitazionali di 2 corpi celesti, di cui uno è un satellite dell’altro, si bilanciano.

Sistema siderale  - sistema di riferimento cartesiano appartenente al piano nel quale si svolge il moto della Luna attorno alla Terra, la cui origine coincide col baricentro del sistema Terra-Luna.

Sistema sinodico  - sistema di riferimento cartesiano con le stesse caratteristiche del sistema siderale e l’asse x passante per i centri della Terra e della Luna (orientato verso quest’ultima).

Velocità rotazionale  - velocità rispetto al sistema sinodico.