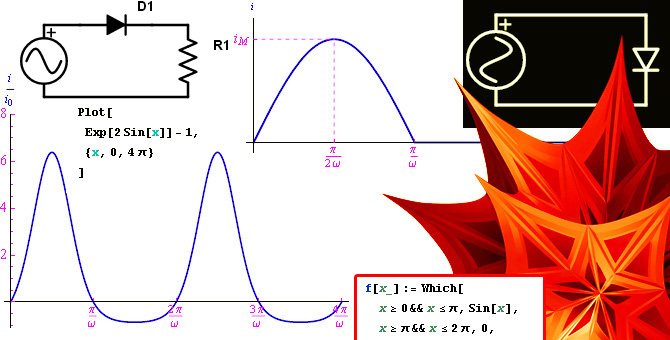
L'Analisi matematica unita all'utilizzo di software di calcolo simbolico/numerico, offre la possibilità di simulare il comportamento circuitale di componenti elettrici tipici, in particolare i componenti non lineari come ad esempio, il diodo a giunzione p-n. Tale paradigma permette il raggiungimento di risultati che sfuggono all'analisi convenzionale che schematizza il componente - nel caso specifico del diodo - attraverso un modello lineare a tratti. Ad esempio, considerazioni di natura analitica unite all'utilizzo di alcuni teoremi di Analisi matematica, permettono di stabilire il range dei valori del carico resistivo di un raddrizzatore a semplice semionda. Per la componente computazionale ci siamo affidati al software Mathematica che implementa la possibilità di integrare simbolicamente equazioni differenziali non lineari, utilizzando alcune funzioni speciali della fisica-matematica.
Introduzione e sintesi degli argomenti
Lo scopo principale del presente articolo è un'assiomatizzazione dell'analisi circuitale di reti elettriche contenenti componenti tipici (resistori, induttori, etc.), con particolare riguardo al diodo a giunzione p-n. Nelle sezioni 2 e 3 passeremo in rassegna le principali proprietà dei componenti elettrici di tipo resistivo, ovvero di quei componenti per i quali esiste una relazione funzionale tra la differenza di potenziale e l'intensità di corrente, definendo alcune grandezze caratteristiche (conduttanza e resistenza differenziale). Verrà quindi discussa la regolarità della funzione che lega la corrente alla tensione, introducendo poi la nozione di tensione di offset, una potenziale discontinuità della derivata della predetta funzione (come effettivamente accade per il modello linearizzato del diodo a giunzione).
Nella sezione 4 - dedicata al comportamento di un circuito raddrizzatore - partendo da condizioni molto generali e richiedendo la continuità della derivata della funzione tensione-corrente (o della sua inversa), giungeremo a un'espressione che è proprio quella del diodo a giunzione. Nel paragrafo 5 mostreremo l'esistenza di un parametro caratteristico del diodo legato a quelli già noti, dalla seguente relazione:
dove le grandezze a numeratore verranno definite in seguito. Per ora osserviamo che VT è una grandezza con le dimensioni di una differenza di potenziale, mentre i0 è la corrente di saturazione inversa. Ebbene la grandezza RT che ha le dimensioni di una resistenza, determina l'effetto raddrizzatore del diodo. Infatti se la resistenza di carico è maggiore (di vari ordini di grandezza) di RT, il diodo risulta "trasparente" alla tensione alternata applicata all'ingresso del circuito raddrizzatore. Nel limite opposto, cioè se la resistenza di carico è nettamente inferiore a RT, si ha un buon effetto raddrizzatore.
Caratteristica tensione-corrente
Assegnato un sistema di assi cartesiani ortogonali, riportiamo in ascisse i valori della tensione v ai capi di un componente di tipo resistivo e in ordinata i valori della corrente i. Variando v e misurando la corrente, vediamo che il punto (v,i) si sposta nel suddetto piano cartesiano descrivendo una curva di equazione:
denominata caratteristica tensione-corrente del componente assegnato.
Osservazione: Indichiamo le differenze di potenziale (d.d.p.) ai capi di un componente con una lettera minuscola del tipo v, a volte dotata di un apice che rappresenta il componente assegnato. Ad esempio, vR denota la d.d.p. ai capi di un resistore, vL la d.d.p. ai capi di un induttore, e così via. Le forze elettromotrici sono invece indicate con lettere maiuscole come, ad esempio, V.
Riguardo alla regolarità della funzione (2) appare ragionevole richiedere la sua continuità nel campo reale R. Infatti, non avrebbe senso considerare una i(v) con punti di discontinuità di prima specie se non addirittura di seconda specie (singolarità). D'altra parte la continuità da sola non basta, nel senso che ci aspettiamo una curva i=i(v) "liscia", per cui imponiamo la derivabilità che, come è noto, garantisce l'esistenza della retta tangente in ogni punto della predetta curva. Questa condizione è vitale in quanto ci permetterà di definire la conduttanza differenziale. Generalizzando ci riferiamo alle cosiddette funzioni di classe Cp su R, ovvero alle funzioni continue in R e dotate di derivate continue fino a un ordine assegnato p. Tale locuzione è simboleggiata da:
ove Cp(R) denota l'insieme delle funzioni reali di una variabile reale che siano continue su tutto R assieme alle derivate fino all'ordine p.
Osservazione: Indicheremo la derivata rispetto al tempo t o rispetto a una variabile del tipo v, con la notazione apicale di Lagrange, cosicchè:
Una richiesta fondamentale è la monotonia in senso stretto della funzione (2).
Condizione 1:
Condizione necessaria affinchè la (2) rappresenti un componente fisicamente realizzabile, è che i(v) sia strettamente crescente in R, ovvero:
In virtù di tale condizione non esiste alcun componente elettrico con caratteristica tensione-corrente come quella riportata in figura 1.
![Figura 1. La funzione i(v) è strettamente decrescente nell'intervallo [v1,v2]: aumentando la differenza di potenziale, la corrente diminuisce.](https://it.emcelettronica.com/wp-content/uploads/2016/07/v_strettamente_crescente1.gif)
Figura 1: La funzione i(v) è strettamente decrescente nell'intervallo [v1,v2]: aumentando la differenza di potenziale, la corrente diminuisce.
Conduttanza differenziale e resistenza differenziale
La rapidità con cui la corrente i aumenta al crescere di v è misurata dalla derivata di i(v):
che si chiama conduttanza differenziale del componente assegnato, ed è la pendenza della curva tensione-corrente. La richiesta che i(v) sia strettamente crescente si traduce in
Un componente si dice circuito aperto se la (2) è la funzione identicamente nulla:
![]()
Cioè per un qualunque circuito aperto, la conduttanza è la funzione identicamente nulla. Esistono alcuni componenti che con buona approssimazione si comportano come circuiti aperti a tratti, nel senso che hanno una conduttanza non nulla solo per un particolare range di valori della differenza di potenziale. Come vedremo in seguito, questo è il caso dei raddrizzatori ideali.
Evidentemente:
Tuttavia è possibile indebolire tale condizione includendo al più le discontinuità di prima specie di g(v), ovvero i punti angolosi della curva i=i(v). Infatti, esistono componenti elettrici con una caratteristica tensione-corrente del tipo:
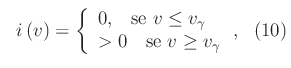
dove vγ è la cosiddetta tensione di offset. In generale, il punto (vγ,0) è di raccordo per la funzione i(v) e per la sua derivata prima, come nell'esempio seguente:
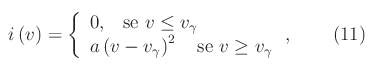
Qui a>0 è un coefficiente che fissa le giuste dimensioni della grandezza i(v), il cui grafico è riportato in figura 2.
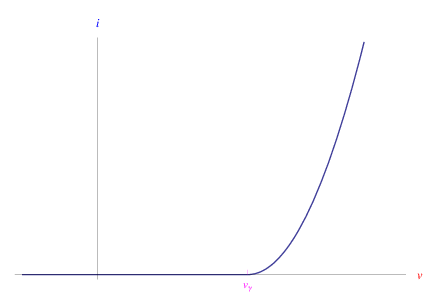
Figura 2: Caratteristica tensione-corrente di un componente con tensione di offset. Il punto corrispondente è di raccordo per la funzione i(v) e per la derivata prima i'(v).
In altri casi, invece, la caratteristica tensione-corrente può avere un punto angoloso in (vγ,0). Ciò si verifica nel modello linearizzato del diodo a [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3016 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.



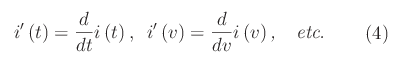
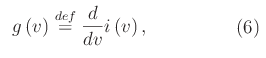
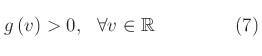





E’ veramente interessante come attraverso una matematica grafica-descrittiva è possibile risalire alla definizione e funzionamento di molti componenti. In fase di design è oltretutto molto utile per tener in considerazione alcuni fenomeni parassiti.
L’articolo è interessante, presenta molti spunti di riflessione e soprattutto mostra ancora una volta la potenza e l’utilità della matematica nello studio dei circuiti elettronici, ma ho alcune perplessità legate al voler “ricostruire” la realtà in maniera assiomatica. Un modello è una astrazione della realtà e la rappresenta nei limiti dell’utilizzo e delle approssimazioni richieste. Voler derivare la realtà a partire dalle proprietà delle funzioni che la descrivono può portare a conclusioni “non realistiche”: ad esempio per la “condizione 1” il diodo tunnel non dovrebbe esistere! (magari premettere una definizione di “componente resistivo” basata su questa condizione avrebbe ristretto il campo di indagine senza incorrere in questa conseguenza).
Un’altra considerazione riguarda la scelta della funzione approssimante che non è necessariamente la logaritmica: sapendo di voler descrivere la caratteristica di un diodo è chiaramente la migliore approssimazione ma si può agevolmente definire il componente “raddrizzatore” con altre semplici funzioni.
Dal punto di vista matematico ho notato, purtroppo, una svista: l’equazione (22) non può “suggerire” nulla perché “non esiste”(la divisione per zero non è definita e non va confusa con una operazione di limite!). Infatti la (20) è valida solo per i’ non nulla: la vera definizione di resistenza differenziale è la (14) che consente di ragionare in termini di operazioni al limite ed arrivare alle conclusioni esposte in (23).
Grazie per il commento. La i(t) non avrà mai un valore esattamente zero, idealmente si, come dice anche l’autore, ma sicuramente sarà un intorno di tale valore (poi qui in realtà dipende dalla bontà del circuito). Quindi la divisione non sarà mai per un numero esattamente pari a zero. In ogni caso nella 23 l’autore esprime proprio il fatto che la r tende all’infinito e quindi la i(t) sta tendendo ad un valore limite pari a zero. Le considerazioni fatte dalla 22 fino alla 24 sono interessanti perché comunque fa vedere un nesso tra la matematica e la funzione del raddrizzatore.
In fisica quantistica ci sono tanti modelli che fanno ancora fatica ad esprimersi nella realtà, l’importante è stabilire le approssimazioni e i fattori di non idealità.
Ho letto solo ora questo commento e rispondo velocemente (vista l’ora tarda).
La (14) e la (22) sono equivalenti. Precisamente, nella (22) si tiene conto della dipendenza temporale di tensione e corrente, per cui esce fuori una funzione composta. La divisione per zero simboleggia, in realtà, un’operazione di passaggio al limite.
Riguardo alla funzione approssimante, una funzione logaritmica non è poi così complicata.
Gianluca Angelone ha scritto:
“L’articolo è interessante, presenta molti spunti di riflessione e soprattutto mostra ancora una volta la potenza e l’utilità della matematica nello studio dei circuiti elettronici, ma ho alcune perplessità legate al voler “ricostruire” la realtà in maniera assiomatica. Un modello è una astrazione della realtà e la rappresenta nei limiti dell’utilizzo e delle approssimazioni richieste. Voler derivare la realtà a partire dalle proprietà delle funzioni che la descrivono può portare a conclusioni “non realistiche”: ad esempio per la “condizione 1” il diodo tunnel non dovrebbe esistere! (magari premettere una definizione di “componente resistivo” basata su questa condizione avrebbe ristretto il campo di indagine senza incorrere in questa conseguenza).”
L’idea di quest’articolo è nata dopo aver dato un’occhiata alla cosiddetta “formulazione assiomatica della termodinamica” che, ovviamente, non c’entra nulla con l’elettronica. Però è interessante l’idea di assiomatizzazione e ho provato ad applicarla all’elettronica con riferimento al diodo a giunzione, in modo da ricostruire le proprietà fondamentali di questo componente. Questa è solo la prima parte dell’articolo. La seconda parte è ancora più lunga e devo sistemarla.
@Gianluca Angelone,
sono d’accordo sulla questione del diodo tunnel: avrei dovuto “restringere” la condizione. Quindi ti ringrazio per la segnalazione.
Riguaro alle altre questioni: la resistenza differenziale è
r(i)=dv/di, dove v(i) è la caduta di tensione ai capi di X.
È chiaro che se applico una d.d.p. variabile nel tempo v(t), avrò una corrente i(t), per cui la formula precedente può essere formalmente scritta come:
r(t)=(dv/dt)*(dt/di) = v'(t)/i'(t), dove l’apice indica la derivata rispetto al tempo. Ho scelto questa strada non per complicare le cose, ma per l’esempio del raddrizzatore ideale sottoposto a un segnale di prova v(t)=V_M*sin(w*t). Questo circuito si comporta come un circuito aperto per tutti i tempi t tali che v(t)0, si ha che per t->0, r(t)->oo. Ma in tutti gli altri istanti t>0, la r(t) assume valori finiti. Nell’articolo originale che poi ho ridotto, mi ci ero arrovellato su questa questione, anche perché ho cercato di assiomatizzare i due casi estremi:
1) X è un corto circuito: v diverso da zero, i=oo
2) X è un circuito aperto: v diverso da zero, i=0.
Il caso 1 è facilmente trattabile: la resistenza elettrica è identicamente nulla. Nel caso 2, invece, la resistenza elettrica è la reciproca della funzione identicamente nulla. È ovvio che tale funzione non esiste nel senso ordinario del termine. Però esiste nel senso delle distribuzioni. Precisamente, è la generalizzazione al continuo di un pettine di Dirac, ovvero di una combinazione lineare di delte di Dirac centrate in istanti assegnati. A ciò si può arrivare nel seguente modo. Immaginiamo un componente X per il quale v(i)=costante*sqrt(i). Lasciamo sospesa la questione: che cavolo di componente è? Esiste? Il nostro è solo un esperimento concettuale che ci permette di capire i meccanismi matematici dietro determinati processi fisici. Se ora immaginiamo di applicare una d.d.p. linearmente crescente v(t)=b*t, dove b>0 è una costante, eseguendo i calcoli si ottiene
r(t)=A/t dove A>0
che è proprio l’andamento visto sopra. Generalizziamo:
r(t)=Sum[A_k/|t-t_k|,{k,0,N}],
cioè la sommatoria di N termini A_k/|t-t_k|. Qui in ogni t_k il componente X è un circuito aperto, giacché r(t) “esplode in singolarità”. Generalizziamo ulteriormente: voglio che X sia un corto circuito per ogni t_k e un circuito aperto per ogni t diverso da t_k. Cioè la r(t) deve divergere per t=t_k e annullarsi per t diverso da t_k. Ma questo altro non è che una combinazione lineare di delte di Dirac ciascuna centrata in t_k. E si chiama pettine di Dirac di ordine N. Quindi:
r(t)=Sum[A_k/delta(t-t_k),{k,0,N}]
Senza perdita di generalità supponiamo che gli istanti t_k siano dati da
t_k=k*(T/N),
dove T>0 è un istante assegnato sufficientemente lungo. Allora riscrivo la resistenza differenziale di questo strano componente X:
r_N(t)=Sum[A_k/deltak*(T/N),{k,0,N}]
Proviamo ad eseguire l’operazione di passaggio al limite per N->+oo. Ciò significa che per un assegnato 0<T+oo]
È chiaro che un oggetto matematico del genere è la generalizzazione al continuo di un pettine di Dirac di ordine N. Formalmente rappresenta una funzione r(t) INFINITA in ogni istante t appartenente a [0,T].
Conclusione: il componente X è un CIRCUITO APERTO.
ps. Queste considerazioni le avevo inizialmente sviluppate, ma poi non le ho inserite nella stesura definitiva perchè mi avrebbero portato fuori tema. Possiamo quindi dire che un circuito aperto ha un comportamento patologico se analizzato in termini puramente matematici.
Correggo una formula:
r(t)=Limit[Sum[A_k/delta(t-k*(T/N)),{k,0,N}],N->+oo]
magari si legge meglio qui http://tinyurl.com/zymwl3m