In un precedente articolo abbiamo trattato ARDUINO e i sensori di temperatura. I sensori sono i componenti fondamentali di un sistema di controllo e l’intento era di arrivare ad implementare un completo sistema di regolazione con ARDUINO. Questa seconda parte tratta la teoria della regolazione. Una parte successiva descriverà il software su ARDUINO che realizza la regolazione di un generico processo ,permettendo di selezionare la tipologia più opportuna a prescindere dalla variabile da controllare.
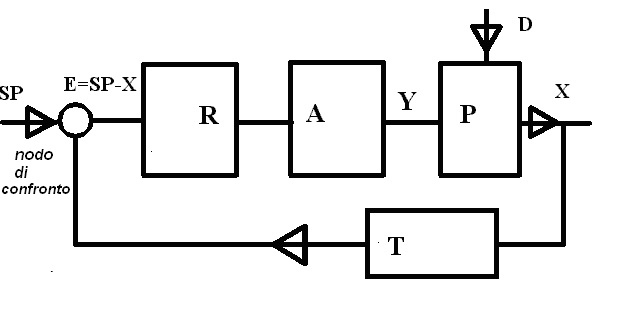
Un sistema di controllo puo' essere schematizzato a blocchi come in figura 1. Un generico processo P è contraddistinto da una grandezza regolata X. La grandezza regolata X è nello schema a blocchi della figura 1 la grandezza d'uscita del processo, che è conseguenza delle condizioni operative che si realizzano all’interno del processo stesso. Questa grandezza viene rilevata dal trasduttore T e perviene al nodo di confronto in cui viene determinata la differenza fra il valore rilevato ed il suo valore di setpoint (il valore della grandezza X impostato nel processo). Il trasduttore rappresenta complessivamente sia l’elemento sensibile che l’insieme dei componenti che convertono questa variazione in un segnale “comprensibile “ alla logica di controllo (tipicamente un segnale elettrico). Il regolatore costituisce l’elemento intelligente che confronta il segnale d’ingresso con il suo valore di setpoint ed agisce sul processo, tramite l’attuatore, attraverso una grandezza regolante che chiameremo Y . L’attuatore può essere un semplice interruttore il cui stato è tipicamente on-off commutando l’accensione o lo spegnimento di una qualsiasi apparecchiatura elettrica. Può essere una valvola, ed in questo caso la grandezza regolante è la sua corsa che ne definisce il grado di apertura. Questo caso corrisponde ad un attuatore modulante, in grado di realizzare una potenza variabile da un valore minimo ad uno massimo. Ammettiamo che il sistema sia inizialmente in una situazione di equilibrio in cui X0 è il valore di setpoint della grandezza regolata e Y0 il corrispettivo valore della grandezza regolante. Un generico disturbo D altera la grandezza regolata X e, di conseguenza, il regolatore cercherà di ripristinare le condizioni impostate di setpoint. Il termine disturbo è significativo di qualunque situazione operativa in grado di alterare la grandezza regolata, senza che possa essere previsto a priori la relazione fra l’entità del disturbo e la variazione della grandezza regolata.
Applicando queste considerazioni alla climatizzazione (riscaldamento) di un ambiente, possiamo affermare che la temperatura dell’ambiente è la grandezza regolata X. Questa varia in funzione dell'equilibrio termico fra la potenza termica introdotta WR e la potenza termica dispersa WD verso l’ ambiente esterno a temperatura inferiore. L'attuatore è il generico elemento scaldante che fornisce la potenza termica WR, che è la grandezza regolante Y. La temperatura esterna è identificabile come il disturbo D che altera l’equilibrio fra WR e WD e quindi la temperatura dell’ambiente. Il primo presupposto della regolazione è la conoscenza dei processi. Una stretta correlazione sussiste fra il tipo di processo e il tipo di regolazione. In un precedente articolo abbiamo trattato ARDUINO e i sensori di temperatura. I sensori sono i componenti fondamentali di un sistema di controllo e l’intento era di arrivare ad implementare un completo sistema di regolazione con ARDUINO. Questa seconda parte tratta la teoria della regolazione. Una parte successivan descriverà il software su ARDUINO che realizza la regolazione di un generico processo, permettendo di selezionare la tipologia più opportuna a prescindere dalla variabile da controllare.
La teoria della regolazione
Figura 1:schematizzazione dei sistemi di controllo
LA REGOLAZIONE ON-OFF
La più semplice, ed anche la più comune delle regolazioni è quella denominata ON-OFF (FIGURA 2). In questo caso l’organo regolante, l’attuatore, puo’ assumere solo 2 stati: acceso(ON) o spento (OFF). E’ comune che questa regolazione venga effettuata, ad esempio, con un termostato. Le condizioni operative sono così definite (si considera un processo di riscaldamento):
-
tSP =temperatura di setpoint (la temperatura voluta ed impostata sul regolatore)
-
∆ =differenziale di temperatura ossia l’intervallo di temperatura fra lo stato di spegnimento(OFF) e quello di accensione(ON)
Quando la temperatura è in salita, l'elemento scaldante viene spento quando t> tSP +∆/2
Quando la temperatura è in discesa (elemento scaldante disattivato), l'elemento scaldante viene riattivato quando t< tSP -∆/2.
Le fasi sono quindi 3:
-
Una fase iniziale in cui la temperatura sale da tiniz a tSP + ∆/2, e l'elemento scaldante è attivo
-
Una fase di raffreddamento in cui l'elemento scaldante è spento e la temperatura si abbassa da tSP +∆/2 a tSP - ∆/2
-
Una successiva fase di riscaldamento in cui l'elemento scaldante è acceso e la temperatura si rialza da tSP -∆/2 a tSP + ∆/2
Nei tempi successivi si alternano le fasi 2 e 3.
A regolare i tempi saranno le costanti caratteristiche del sistema. La costante di tempo CT=MC/KS regola il tempo di raffreddamento tC e quello di riscaldamento tH mentre il rapporto W/KS regola il solo tempo di riscaldamento tH, che è quindi il solo ad essere influenzato dalla potenza termica scaldante W.
Un aumento della potenza termica W comporta un tempo tH minore, mentre un aumento della costante di tempo comporta sia un maggior tempo tH che tC. Un aumento del differenziale comporta un aumento di entrambi i tempi tH e tC e una minore frequenza di intervento del termostato, viceversa una diminuzione.
Con questo tipo di funzionamento la temperatura t sarà uguale a quella di setpoint solo quando la curva della temperatura tocca la linea t=TSP .
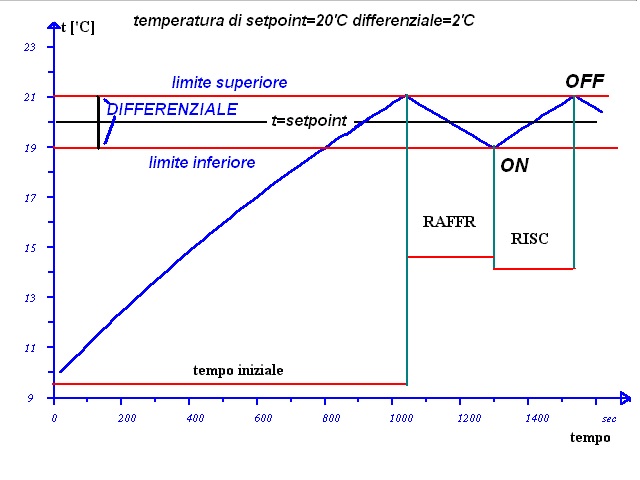
Figura 2: la temperatura in funzione del tempo nella regolazione ON-OFF
LA REGOLAZIONE PROPORZIONALE
Nella regolazione proporzionale tra l'azione regolante, il cui valore chiameremo y ed il valore della variabile regolata, che chiameremo x, sussiste il legame:
Y-Y0=KP(x-x0)
Dove KP è una costante di proporzionalità, x0 il valore di setpoint della variabile regolata, y0 il corrispondente valore della variabile regolante. Il campo di variazione della variabile regolata viene denominato banda proporzionale BP, mentre il campo di variazione della variabile regolante Y viene denominato banda d’azione.
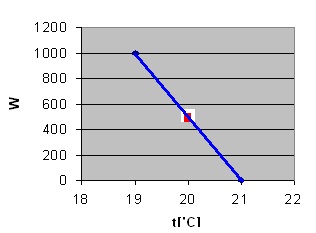
Figura 3: grafico della potenza termica in funzione della temperatura ambiente per l’ azione proporzionale
Con riferimento alla figura 3 la banda proporzionale BP è in questo caso 2°C, ±1°C rispetto al setpoint=20°C(setpoint al centro della banda proporzionale). La banda d’azione è 1000 watt, corrispondente alla variazione di potenza termica, tra i valori estremi della banda proporzionale t=20+1°C =21°C (0 watt) e t= 20-1°C=19°C (1000 watt). Più spesso la banda d’azione si esprime in percentuale rispetto al valore massimo e quindi la variabile Y varierebbe da 0 al 100%. Ad un aumento della variabile regolata corrisponde una diminuzione della variabile regolante: è l’azione cosiddetta normale. Viceversa, il regolatore è ad azione invertita (come potrebbe essere ad esempio nel caso del condizionamento estivo). La figura 4 rappresenta entrambi i casi.
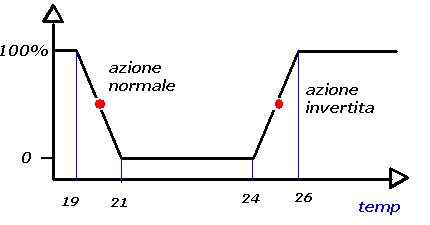
Figura 4: azione normale (riscaldamento invernale) e invertita (condizionamento estivo)
Il regolatore R confronta la temperatura di setpoint tsp impostata con la temperatura del processo t e modula la potenza termica scaldante per il processo. La retta visualizza la corrispondenza fra la grandezza regolante (la potenza termica) e la grandezza regolata (la temperatura). Nella posizione di setpoint la potenza termica W è 500 watt, corrispondente ad una temperatura esterna di 7,5 °C. Se le condizioni di equilibrio del sistema vengono alterate, ad esempio per una diminuzione della temperatura esterna, la potenza termica dispersa aumenta con conseguente diminuzione della temperatura ambiente. La nuova condizione di equilibrio non potrà più sussistere per il valore di temperatura di setpoint ma dovrà spostarsi, secondo la retta della figura 1 verso sinistra, con un aumento della potenza termica. La tabella 1 riporta le condizioni che si verificano, al variare della temperatura esterna, con due diversi valori di banda proporzionale. Lo scostamento permanente della variabile regolata , denominato OFFSET, è tanto minore quanto minore è la banda proporzionale.
Con banda proporzionale=2°C
test[°C]
tamb[°C]
Potenza termica
[watt]
-5
19,07
960
7,5
20
500
20
20,93
37
Con banda proporzionale=1°C
Test['C]
Tamb['C]
Potenza termica[watt]
-5
19,52
981
7,5
20
500
20
20,48
20
Tabella 1: valori di temperatura e potenza termica nella regolazione proporzionale al variare della temperatura esterna
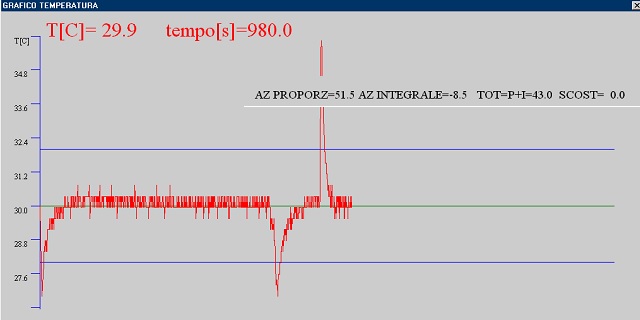
Nell’immagine di presentazione il grafico della temperatura con azione proporzionale+integrale. BP=4°C setpoint=32°C , tempo integrale 1 minuto. Si noti l’effetto dei due disturbi( uno con abbassamento della temperatura e l’altro con innalzamento)
L’ AZIONE INTEGRALE
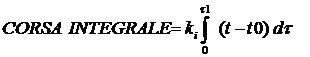
dove (t-t0) è lo scostamento, dt l'intervallo di tempo, kI una costante, t il tempo generico. Nell'esempio il valore di kI è di 0,003 . L'integrale fra il tempo zero ed il tempo t dello scostamento è uguale all'area sottesa la curva che rappresenta l'andamento dello scostamento stesso in funzione del tempo. L'azione integrale, attraverso una costante kI è pertanto proporzionale a questa area che rappresenta in pratica l’errore .
Riprendiamo l'esempio e adottiamo ora una regolazione PI con i valori di:
-
BP=2°C
-
setpoint=20°C
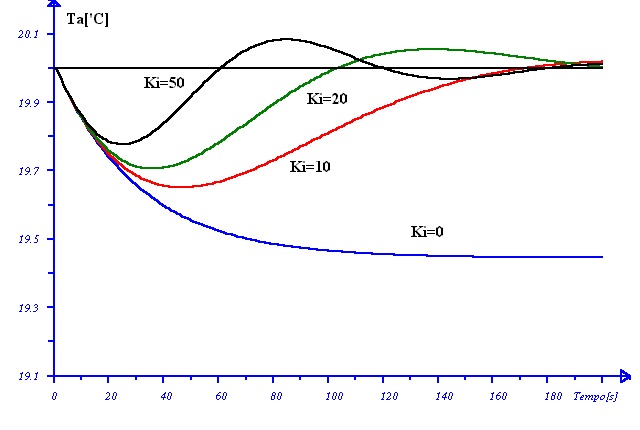
Figura 5: andamento della temperatura per diversi valori di Ki.
Supponiamo che la temperatura esterna test vari bruscamente da 7,5 a 0°C. La figura 5 rappresenta l'andamento della temperatura del corpo nei casi in cui la costante integrale Ki abbia i valori indicati in figura. Quando Ki=0 l'azione integrale è nulla e quindi ricadiamo nella sola azione proporzionale: vi è uno scostamento permanente dal setpoint. All'aumentare di Ki gli scostamenti massimi diminuiscono e aumentano le oscillazioni, in ogni caso la temperatura tende a tornare al valore di setpoint. In questo esempio la potenza termica disponibile WMAX è pari alla potenza termica dispersa WD con un salto termico di 25°. Quindi, nelle condizioni sopra citate (salto termico 20°C) essendo WMAX>WD la temperatura del corpo può salire oltre i 20°C. Quando la potenza termica dispersa aumenta la temperatura del corpo, essendo W<Wd diminuisce. L’azione proporzionale interviene aumentando la potenza W. Essendo comunque WD>W la temperatura diminuisce. In funzione del tempo cresce l’azione integrale, che si somma all’azione proporzionale. In corrispondenza del valore minimo della temperatura raggiunta dal corpo, la somma delle 2 azioni uguaglia la potenza termica dispersa. Essendo ora t<20°C si ha W>WD e la temperatura aumenta fino a raggiungere asintoticamente il valore di setpoint. Nella tabella 2 sono riportati i dati della figura 6 che è relativo al caso ki=50 della figura 5.
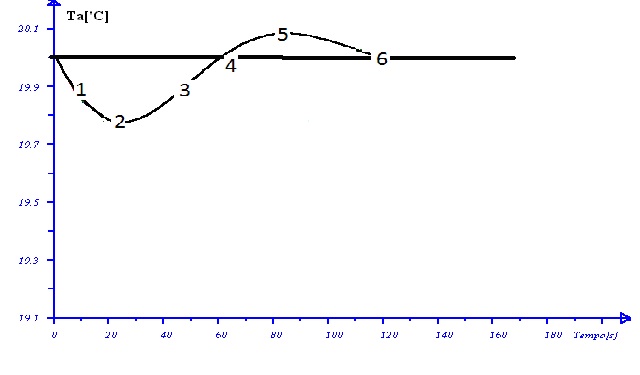
Figura 6: temperatura in funzione del tempo con azione PI
L’AZIONE DERIVATIVA
L'azione derivativa aggiunge un'ulteriore azione di controllo. Con riferimento all'esempio 2, regolazione di livello, l’azione derivativa sarebbe data da:
azione derivativa = Kd dh/dt
Cioè proporzionale alla velocità di variazione del livello. L'azione derivativa, che è teoricamente immediata, anticipa la variazione della variabile controllata determinando quindi una diminuzione dell'ampiezza degli scostamenti rispetto alla regolazione integrale.
punto
Tempo
secondi
temperatura °C
scostamento
area
area tot
az integrale
az proporz
az totale
1
9
19,90
0,10
-0,49
-0,49
0,41
55,22
55,63
2
23
19,78
0,22
-2,30
-2,79
2,32
61,09
63,41
3
44
19,88
0,12
-3,45
-6,24
5,20
55,87
61,07
4
61
20,00
0,00
-1,01
-7,25
6,04
50,00
56,04
5
86
20,09
-0,09
1,14
-6,10
5,09
45,43
50,52
6
117
20,00
0,00
1,43
-4,68
3,90
50,00
53,90
Tabella 2: le aree totali sono quelle sottese dalla curva di figura 6 relativamente alla retta di equazione t=20°C.
CONCLUSIONI
Nel prossimo articolo implementeremo la teoria della regolazione di cui abbiamo discusso oggi su ARDUINO, sviluppando un controllore universale, in cui è possibile selezionare il tipo di regolazione on off, ad uno o due stadi, proporzionale, proporzionale integrale, ed i parametri (setpoint, banda proporzionale etc). Riprendendo l'articolo precedente, attraverso Processing, il PC potrà comunicare con Arduino e visualizzare il grafico temperatura-tempo.


Trovo interessante un articolo che tratta in maniera pratica la teoria della regolazione, ed approfitto per aggiungere alcune considerazioni.
In riferimento al controllore ON-OFF, anche se si tratta di gergo, per completezza si può dire che il “differenziale” si chiama anche “isteresi” e questo tipo di controllore è detto anche controllore ad isteresi.
In figura 2, sembra che la temperatura immediatamente inizi a scendere appena si spegne la sorgente. Forse può essere una buona approssimazione per una pompa di calore, ma in un sistema di riscaldamento “classico” anche se si spegne la caldaia, i termosifoni continuano ad introdurre energia nel sistema e quindi la temperatura continua a salire per qualche tempo prima di invertire la pendenza.
Si fa riferimento, per il prossimo articolo, a controllori a “due stadi” proporzionali integrali. Forse sono troppo legato al gergo ma parlare di “stadi” mi fa pensare a sistemi in “cascata” (o serie) mentre qui le azioni si sommano (in parallelo).
Vorrei soffermarmi sull’azione derivativa. Non è citata negli sviluppi futuri, spero sia una svista perché sarebbe più completo parlare di un PID (di cui il PI è un caso particolare con Kd=0).
Non capisco dove sia l’esempio 2. In ogni caso si intuisce, ma sarebbe il caso di dirlo esplicitamente, che l’azione derivativa agisce sulla derivata dell’uscita e non dell’errore, come per gli altri controlli in retroazione. Questo per limitare l’azione di controllo ed evitare una possibile sollecitazione eccessiva degli attuatori.
mi piace di più il termine differenziale che esprime meglio l’azione on-off sull’intervallo di temperatura. La repentina discesa della temperatura dipende dal tipo di sistema (ordine 0 od 1).Il grafico è valido per sistemi con una sola massa concentrata.
gli stadi si riferiscono all’azione in cascata su più attuatori e non alle azioni di regolazione. L’esempio 2 è una regolazione di livello. Nell’articolo si parla di azione D come dh/dt e quindi proprio di derivata
Salve volevo chiederle se ha poi più realizzato il codice implementativo in arduino.
Che dh/dt sia una derivata è lapalissiano! Il punto è che, volendo presentare una teoria della regolazione a chi non la conosce (altrimenti non si scriverebbe un articolo!) , andrebbero puntualizzate alcune cose.
In particolare l’altezza in un regolatore di livello rappresenta l’uscita (variabile controllata), e dh/dt è la derivata dell’uscita e non dell’errore. Come già detto nell’altro commento, sarebbe stato utile spiegare perché l’azione derivativa agisce sull’uscita e non sull’errore, ovvero perché non è d(h-h0)/dt, se h0 è riferimento. Ribadisco che anche se vogliamo un riferimento costante (la cui derivata è nulla) in realtà c’è una discontinuità all’accensione e questo (a meno di non filtrare il riferimento) provoca una forte sollecitazione agli attuatori (matematicamente sarebbe un impulso). A maggior ragione il problema si presenta nel caso in cui si voglia variare il riferimento in maniera discreta, ad esempio tramite una manopola a scatti, dove ad ogni variazione c’è la presenza dell’impulso nel segnale di controllo.
Un’ultima nota, se si dice “Con riferimento all’esempio 2” (articolo determinativo) si rimanda a qualcosa di già introdotto, ovvero l’esempio deve essere stato descritto in precedenza, da qui la mia domanda nel commento. Infine la “regolazione di livello” non è un concetto “universale” o “univoco”, quindi qualche parola in più per descrivere il sistema (ad esempio si può controllare la portata in ingresso, quella in uscita o entrambe, ecc.) con qualche dato numerico ed un grafico per mostrare l’effetto dell’azione derivativa, come fatto nel resto dell’articolo per le azioni P ed I nel caso di un sistema termico sarebbe stato utile ed avrebbe reso l’articolo più leggibile.
l’articolo non può essere esaustivo per la complessità del tema trattato , che meriterebbe più di qualche pagina.Come docente di automazione impiego almeno 1 mese per spiegare questi argomenti
l’articolo sulla implementazione è già stato inviato, provi a chiedere ai responsabili se verrà pubblicato o meno
L’articolo è in fase di revisione.
Salve volevo chiederci se l’articolo con il codice implementativo è stato pubblicato..
Ecco l’articolo con allegato il codice
http://it.emcelettronica.com/la-regolazione-di-temperatura-con-arduino