Implementare la FFT con Python

Per rendere più veloce il calcolo della trasformata DFT, l'algoritmo FFT venne sviluppato da James Cooley e John Tukey. Questo algoritmo è considerato uno degli algoritmi più importanti del 20° secolo. La trasformata DFT impiega N*N moltiplicazioni complesse per fornire i risultati, mentre l'algoritmo FFT impiega solo (N/2)*logN moltiplicazioni. Tale riduzione nel numero delle operazioni richieste diventa un vantaggio significativo quando il numero dei campioni è elevato. In questo articolo faremo un'analisi dell'algoritmo FFT e vedremo come implementarlo da zero utilizzando il linguaggio di programmazione Python.

Introduzione

La classica trasformata di Fourier permette di ottenere una rappresentazione nel dominio delle frequenze di un qualsiasi segnale. Per poter usufruire di questo strumento matematico su un calcolatore elettronico occorre una versione a tempo discreto, la cosiddetta DFT. Ma, anche se utilizzabile in teoria su un calcolatore, la DFT si dimostra inefficiente nella pratica, a causa dell'eccessivo carico computazionale. La FFT è un potente strumento che rende l'analisi spettrale mediante DFT, computazionalmente possibile. A causa dell'importanza della FFT in tanti campi, Python contiene molti strumenti standard e wrapper per calcolarla. Sia NumPy che SciPy hanno wrapper della libreria FFTPACK estremamente ben collaudati, che si trovano rispettivamente nei sottomoduli numpy.fft e scipy.fftpack. La FFT più veloce dovrebbe trovarsi nel pacchetto FFTW, disponibile anche in Python tramite il pacchetto PyFFTW. Per il momento, tuttavia, lasciamo da parte queste implementazioni. In questo articolo invece andremo ad analizzare le caratteristiche dell'algoritmo FFT e di come implementarlo da zero mediante il linguaggio di programmazione Python. Per chi avesse poca esperienza con Python, utilizzeremo uno strumento utilissimo per la didattica, ovvero Colaboratory.

Colaboratory o, in breve, "Colab", permette a chiunque di scrivere ed eseguire codice Python nel proprio browser con i seguenti vantaggi:

Nessuna configurazione necessaria
Accesso gratuito alle GPU
Condivisione semplificata

Per poter seguire il file passo-passo ed osservare i risultati prodotti, basterà entrare nel proprio account Google e cliccare sul seguente LINK.

L'algoritmo FFT

Ciò che consente alla FFT di essere computazionalmente efficiente è il fatto di sfruttare le simmetrie presenti nella DFT. Se si riesce a dimostrare analiticamente che una parte di un problema è semplicemente correlata ad un'altra, si può calcolare il sotto-risultato solo una volta e risparmiare quel costo computazionale. Supponiamo che x(n) sia una N-sequenza, ovvero soddisfi la condizione x(n)=0 per ogni n<0 e n≥N, allora definiamo X(k) come la Trasformata Discreta di Fourier (DFT).

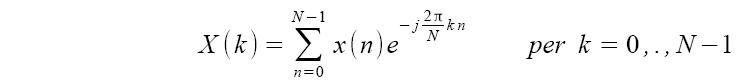X(k) è anch'essa una N-sequenza.

Una semplice implementazione della FFT procede con la separazione della sequenza di dati di input x (n) in due parti: elementi pari ed elementi dispari indicizzati. Allora, la X(k) diventa:

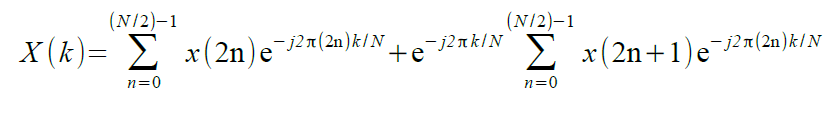Ponendo W_N = e^(-j2π/N) per rappresentare il fattore di fase costante con N, avremo che l'equazione si può riscrivere come:

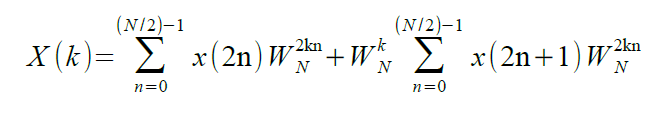Per non appesantire la lettura non dimostreremo la seguente affermazione, ovvero che W²_N = W_N/2, allora X(k) diviene:

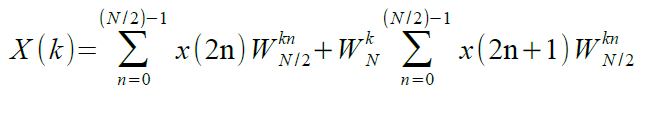Inoltre, si potrebbe dimostrare, ma non lo faremo, che X(k+N/2) è dato da:

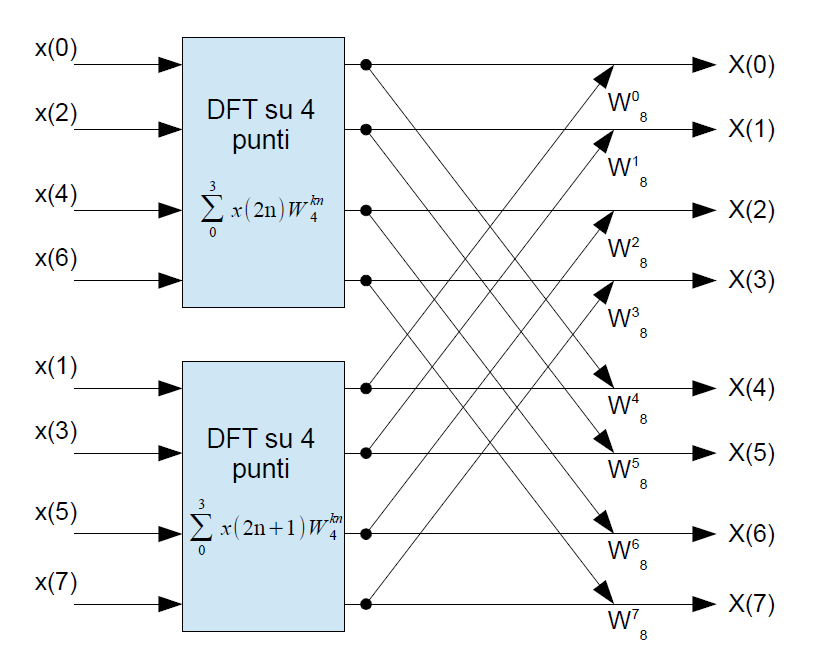
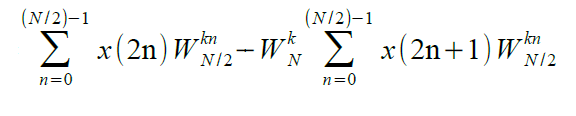Comparando le equazioni di X(k) e X(k+N/2) si evince che l'unica differenza tra le due sta nel segno del fattore W^k_N. Possiamo allora affermare che per una DFT su N punti, basta eseguire 2 DFT su N/2 punti per ottenere le prime N/2 uscite e riutilizzarle, operando solo sul fattore W, per ottenere le ultime N/2 uscite. Per N = 8 possiamo visualizzare graficamente, come in Figura 1, le considerazioni fatte.

Figura 1: Rappresentazione grafica della simmetria presente nella DFT su 8 punti

A questo punto, possiamo andare oltre e pensare di suddividere le due DFT su 4 punti in quattro DFT su 2 punti. Analogamente a quanto fatto in precedenza, segmentiamo gli ingressi delle DFT a 4 punti nelle loro componenti pari e dispari. Procedendo in questo modo iterativamente si arriva al punto di avere DFT a 2 punti in cui non è possibile realizzare ulteriori risparmi computazionali. Questo è il motivo per cui il numero di punti su cui effettuare la FFT è limitato ad essere una potenza di 2. Alla fine il carico computazionale passerà da N*N moltiplicazioni richieste per la DFT alle (N/2)logN moltiplicazioni richieste dalla FFT. Che, per N=8, significa passare da 64 a 12 operazioni. La FFT non è un'approssimazione di una DFT, ma è la DFT con un numero ridotto di operazioni aritmetiche necessarie. Quindi, la sua corretta esecuzione non comporta perdite di accuratezza rispetto alla DFT.

Calcolare la DFT in Python

L'espressione della DFT non è altro che una semplice operazione lineare. Si tratta di una moltiplicazione matrice-vettore del tipo X = M·x dove X è un vettore le cui componenti sono le N DFT X(k), M è una matrice NxN dove il generico elemento M_nk = e^-j2πkn/N, e x è il vettore degli x(n) della N sequenza da analizzare. Con questo in mente possiamo scrivere il codice Python che implementa la DFT, come segue:

#Calcolo della DFT
import numpy as np
import matplotlib.pyplot as plt
def DFT_slow(x):
    x = np.asarray(x, dtype=float) #converte x in un array
    N = x.shape[0]                 #estrae la dimensione di x
    n = np.arange(N)               #crea una successione da 0 a N
    k = n.reshape((N, 1))          #la trasposizione di n
    M = np.exp(-2j * np.pi * k * n / N) #matrice dei fattori esponenziali
    return np.dot(M, x)            #array ottenuto come prodotto scalare

Possiamo controllare il risultato confrontandolo con la funzione FFT integrata di numpy np.fft.fft(x):

#Verifico se DFT_slow() fornisce risultati accurati
x = np.random.random(1024)                 #crea un array di 1024 numeri casuali
np.allclose(DFT_slow(x), np.fft.fft(x))    #restituisce True se i due array sono uguali elemento per elemento

Se gli array calcolati dalle due implementazioni risultano uguali elemento per elemento, allora np.allclose() restituirà TRUE. Solo per confermare la lentezza del nostro algoritmo, possiamo confrontare i tempi di esecuzione di questi due approcci:

%timeit DFT_slow(x)
%timeit np.fft.fft(x)

Il nostro approccio (122 ms) risulta essere oltre 1000 volte più lento rispetto alla funzione integrata di numpy (19,8 μs). Il risultato non sorprende visto che l'implementazione dell'algoritmo è così semplicistica. Ma questo non è il caso peggiore. Per un vettore di input di lunghezza N, il nostro algoritmo lento richiede un numero di operazioni aritmetiche dell'ordine di O[N²], mentre la FFT richiede un numero dell'ordine di O[NlogN]. Ciò significa che per N = 106 elementi, la FFT dovrebbe completare il calcolo in circa 50 ms, mentre il nostro lento algoritmo richiederebbe quasi 20 ore.

Calcolo ricorsivo della FFT

Risulta quindi ovvio che calcolare la DFT in modo classico sia inapplicabile nella pratica. Occorre sfruttare le simmetrie presenti nella trasformata per implementare una versione più veloce: la FFT. La trasformata veloce di Fourier può essere implementata in diversi modi, uno dei quali è quello ricorsivo. L'algoritmo ricorsivo può essere implementato molto rapidamente in Python, riutilizzando il nostro codice per il calcolo della DFT lenta, quando la dimensione del sottoproblema diventa adeguatamente piccola:

def FFT(x):
    """Implementazione ricorsiva della FFT"""
    x = np.asarray(x, dtype=float)
    N = x.shape[0]
    if N % 2 > 0: #valuto il resto
        raise ValueError("size of x must be a power of 2")
    elif N <= 32:  # questa soglia andrebbe ottimizzata
        return DFT_slow(x)
    else:
        X_even = FFT(x[::2])   #viene riapplicato algoritmo sugli elementi pari
        X_odd = FFT(x[1::2])   #viene riapplicato algoritmo sugli elementi dispari
        factor = np.exp(-2j * np.pi * np.arange(N) / N)
        return np.concatenate([X_even + factor[:int(N/2)] * X_odd,
                               X_even + factor[int(N/2):] * X_odd])

In sostanza, vediamo cosa avviene nel codice per l'implementazione ricorsiva della FFT:

Nel primo if viene valutato se N è divisibile per 2. L'algoritmo dà errore se N non è divisibile per 2.
In caso contrario l'algoritmo valuta se N è minore o uguale ad una certa soglia (32). Se si, allora viene applicata la DFT lenta che è anche il risultato della funzione FFT(x).
Se maggiore della soglia, invece, si procede a riapplicare la funzione FFT(x) agli elementi pari e a quelli dispari per poi concatenare il tutto per il risultato finale.

Anche in questo caso effettuiamo una rapida verifica che il nostro algoritmo produca il risultato corretto e compariamo quindi i tempi di esecuzione dei tre approcci: DFT lenta, FFT ricorsiva e FFT integrata in numpy.

x = np.random.random(1024)
np.allclose(FFT(x), np.fft.fft(x))

%timeit DFT_slow(x)
%timeit FFT(x)
%timeit np.fft.fft(x)

Il nuovo algoritmo è più veloce (7,14 ms) della prima versione (122 ms) di oltre un ordine di grandezza. Si noti, però, che non siamo ancora arrivati alla velocità dell'algoritmo FFT integrato in numpy (19,8 μs), e questo è prevedibile. L'algoritmo FFTPACK dietro la FFT di NumPy è un'implementazione in Fortran che ha ricevuto anni di modifiche e ottimizzazioni. Una buona strategia per accelerare il codice quando si lavora con Python/NumPy è vettorializzare i calcoli ripetuti ove possibile. Possiamo farlo e nel frattempo rimuovere le chiamate di funzioni ricorsive e rendere il nostro codice ancora più efficiente.

[...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2061 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.

Introduzione

L'algoritmo FFT

Calcolare la DFT in Python

Calcolo ricorsivo della FFT

Ti potrebbe interessare anche:

Autore:

Andrea Garrapa

Scrivi un commento Annulla risposta