Per poter quantificare la bontà delle prestazioni di un convertitore analogico - digitale (ADC), ci si affida all'analisi di alcuni parametri dinamici. Il calcolo di questi parametri è frutto dell'applicazione sul segnale di uscita del convertitore, di uno strumento matematico noto come Trasformata Rapida di Fourier (FFT). In questo articolo faremo una panoramica sui principali parametri dinamici utilizzati nello studio delle performance di un ADC, e poi vedremo come valutarli grazie alla FFT. In particolare ci soffermeremo su come valutare il rapporto Segnale-Rumore (SNR) in presenza di un'analisi non coerente. Questa rappresenta la peggiore delle situazioni in cui ci si possa trovare quando si vuole quantificare la precisione di un convertitore analogico - digitale. Applicando opportune finestre al segnale è possibile mitigare questo fenomeno. Nell'articolo vedremo quindi quale finestra sia meglio utilizzare per risolvere le problematiche relative a tale contesto.
Parametri dinamici
I parametri dinamici su cui focalizzeremo la nostra analisi sono i seguenti: SNR (Signal to Noise Ratio), SINAD (Signal to Noise and Distortion Ratio), ENOB (Effective Number Of Bits) e THD (Total Harmonic Distortion).
Signal to Noise Ratio (SNR)
Dato un sistema che effettui una qualsiasi operazione su un segnale, si definisce rapporto segnale - rumore come il rapporto tra la potenza del segnale PS e quella del rumore PN introdotta dal sistema:
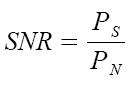 Supponiamo che il sistema in questione sia un ADC con una risoluzione pari a N, e che il segnale d'ingresso sia una sinusoide a fondo scala. Se la quantizzazione del convertitore è di tipo ideale, allora il solo rumore presente in uscita sarà quello di quantizzazione. Quindi definito Δ come l'intervallo di quantizzazione avremo che la potenza del segnale s(t) = (Δ2N/2)sin(2πfst) sarà pari al quadrato del suo valore efficace PS = (Δ2N/2√2)2 , mentre essendo il rumore un processo stocastico di tipo uniforme avrà potenza pari alla sua varianza PN = (Δ/2√3)2. Sostituendo nella formula del SNR ed applicando 10log10 per ottenere il risultato in dB avremo:
Supponiamo che il sistema in questione sia un ADC con una risoluzione pari a N, e che il segnale d'ingresso sia una sinusoide a fondo scala. Se la quantizzazione del convertitore è di tipo ideale, allora il solo rumore presente in uscita sarà quello di quantizzazione. Quindi definito Δ come l'intervallo di quantizzazione avremo che la potenza del segnale s(t) = (Δ2N/2)sin(2πfst) sarà pari al quadrato del suo valore efficace PS = (Δ2N/2√2)2 , mentre essendo il rumore un processo stocastico di tipo uniforme avrà potenza pari alla sua varianza PN = (Δ/2√3)2. Sostituendo nella formula del SNR ed applicando 10log10 per ottenere il risultato in dB avremo:
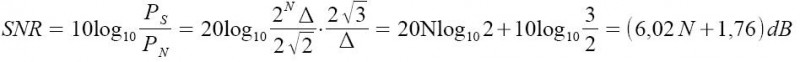 In sostanza abbiamo trovato un limite superiore al rapporto segnale rumore per un ADC di risoluzione N. Un ADC reale non potrà mai avere un SNR maggiore o uguale a questo limite.
In sostanza abbiamo trovato un limite superiore al rapporto segnale rumore per un ADC di risoluzione N. Un ADC reale non potrà mai avere un SNR maggiore o uguale a questo limite.
Total Harmonic Distortion (THD)
La distorsione armonica è quel fenomeno per cui un sistema produce delle frequenze in uscita, che non sono presenti nel segnale d'ingresso. La THD si misura come rapporto tra la somma quadratica delle ampiezze V(jf0) di un certo numero n di armoniche e l'ampiezza della fondamentale V(f0).
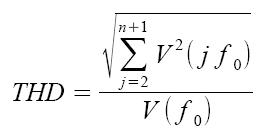 SIgnal to Noise And Distortion (SINAD)
SIgnal to Noise And Distortion (SINAD)
Il SINAD è un ottimo indicatore delle performance dinamiche di un ADC poichè tiene conto di tutte le componenti di rumore e distorsione, ed infatti è ottenuto semplicemente dalla somma di SNR e THD.
![]() Nella sua banalità, questo parametro trova la sua utilità nel calcolo di un altro indicatore dinamico, cioè l'ENOB.
Nella sua banalità, questo parametro trova la sua utilità nel calcolo di un altro indicatore dinamico, cioè l'ENOB.
Effective Number Of Bits (ENOB)
Dato un convertitore analogico digitale con risoluzione N, il parametro ENOB ci dice quale sia l'effettiva risoluzione dell'ADC. L'effettiva risoluzione del convertitore sarà sicuramente inferiore a quella reale, a causa del rumore e delle distorsioni. ENOB si calcola con la seguente formula:
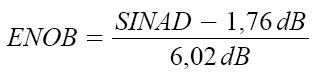 Trasformata Rapida di Fourier (FFT)
Trasformata Rapida di Fourier (FFT)
Per misurare i parametri dinamici definiti nel paragrafo precedente, viene utilizzato uno strumento [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2708 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.








Salve,
A parte puntualizzare l’interessante analisi svolta sull’articolo (conosciuto) tramite la rivista Firmware), volevo segnalare che sulla rivista stessa (ovvero nel suo PDF) la Figura 5 è mancante.
Tendo a pensare sia solamente una questione di spazio editoriale.
Grazie
Paolo Bisighin
Grazie a lei Paolo
Grazie della segnalazione. Provvederemo il prima possibile.