
Dietro ogni criptovaluta esiste sempre un algoritmo di consenso, il cui compito è assicurare che ogni transazione sia correttamente verificata e validata prima di essere inserita nella blockchain. Non esiste a priori un algoritmo perfetto, ognuno ha i suoi particolari pregi, punti di forza e difetti. Scopriamo in questo articolo quali sono le caratteristiche e le differenze tra i due principali algoritmi di consenso e quali altri schemi sono stati portati alla ribalta dalle criptovalute di ultima generazione.
Introduzione
Tutti noi sappiamo che ciascuna transazione inserita nella blockchain (per comodità facciamo riferimento al Bitcoin, la criptovaluta che attualmente detiene la maggiore capitalizzazione) deve essere stata preventivamente verificata e validata. Una volta inserita, la transazione diventa infatti immutabile, impossibile da modificare o contraffare. Questo meccanismo è reso possibile dalla presenza di un algoritmo di consenso, definibile come lo strumento attraverso il quale è possibile trovare un accordo sulla validità di un dato operando all'interno di un sistema distribuito. Gli algoritmi di consenso hanno pertanto il compito di assicurare l'affidabilità in sistemi o reti che coinvolgono nodi multipli; applicati al mondo delle criptovalute, garantiscono la sicurezza e la natura decentralizzata del sistema. Le criptovalute rappresentano infatti un modo decentralizzato per scambiare denaro o servizi utilizzando la rete internet, non esiste alcuna struttura centrale, sia essa una banca o altra istituzione finanziaria o governativa, che possa eseguire un controllo su di esse. Gli algoritmi di consenso sono il cuore della natura decentralizzata delle criptovalute, facilitando il comune accordo tra gli utenti di tutto il mondo su quali siano le regole e come vadano applicate.
Il problema dei generali bizantini
Il problema dei generali bizantini rappresenta uno dei nodi cruciali che ogni sistema distribuito deve affrontare affinché possa operare in modo sicuro ed efficiente. Per un sistema di questo tipo è infatti essenziale la proprietà di tolleranza ai guasti bizantini (indicata anche con il termine BFT, acronimo di Byzantine Fault Tolerance), intendendo con ciò la capacità del sistema stesso di operare correttamente anche in presenza di un guasto causato dal problema dei generali bizantini. Gli effetti prodotti dal problema dei generali bizantini sono meglio osservabili nei sistemi distribuiti (tipicamente nelle reti di computer). In questi scenari accade spesso che il guasto (o l'alterazione voluta) di un componente generi dei conflitti sulle informazioni presenti in parti differenti del sistema, creando una situazione di inconsistenza dei dati. L'inconsistenza, a sua volta, può essere risolta o superata soltanto raggiungendo un consenso condiviso. Questa problematica è stata formalmente espressa nel 1982 nell'articolo "The Byzantine's Generals' Problem" ad opera di Lamport, Shostak, e Pease. Gli autori formularono per la prima volta il problema esponendolo sotto forma di metafora, che ora descriveremo. Si supponga che un gruppo di generali, ciascuno a capo di una divisione dell'esercito bizantino, debba decidere se attaccare o meno una città nemica. I generali possono comunicare tra di loro esclusivamente tramite dei messaggeri. Qualunque sia la decisione presa, occorre che questa sia condivisa da ogni generale, in quanto un attacco non perfettamente coordinato avrebbe conseguenze persino peggiori di una ritirata. Il problema, già di per sè complesso, è ulteriormente aggravato dalla potenziale presenza sia di generali traditori (i quali cercano di impedire un accordo tra i generali fedeli tramite il sabotaggio) che di messaggeri inaffidabili (i quali potrebbero agire intenzionalmente o inconsapevolmente contro la giusta causa). Occorre pertanto trovare una soluzione che soddisfi i seguenti requisiti:
- tutti i generali fedeli devono concordare uno stesso piano di azione
- un numero ristretto di traditori non può impedire ai generali fedeli di mettere in azione il proprio piano.
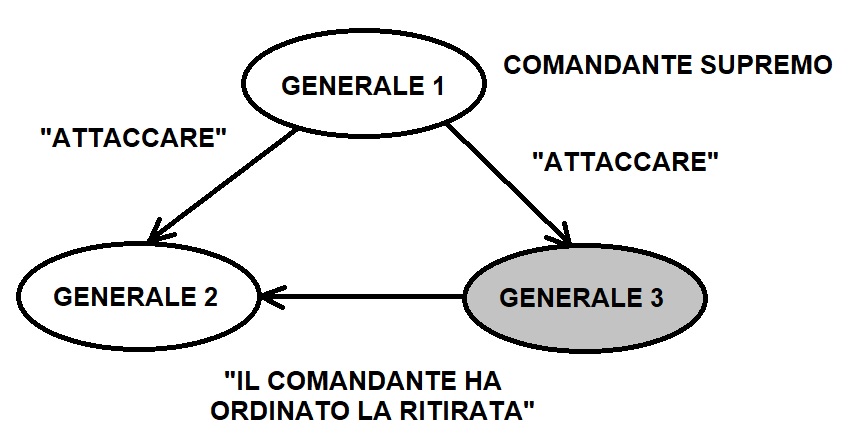
In Figura 1 possiamo osservare la seguente situazione: dei tre generali, il primo ha anche il comando supremo delle forze, mentre il terzo (evidenziato in grigio) è un generale traditore che mente in merito ai comandi ricevuti. Le conseguenze per il generale 2 sono disastrose, in quanto riceve ordini incongruenti tra loro dal comandante e dal generale 3.
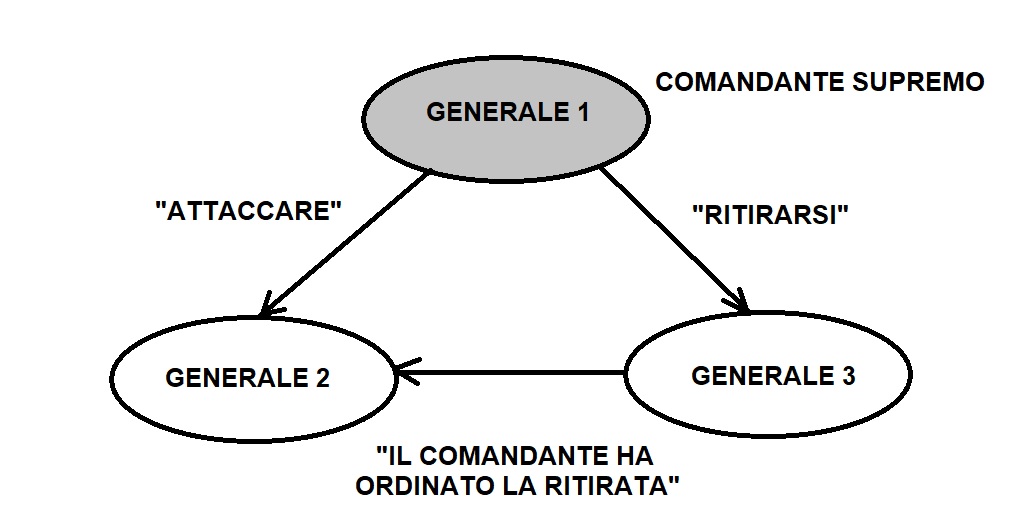
Analoga, anche se più grave dal punto di vista morale, è la situazione rappresentata in Figura 2: in questo caso è il comandante ad essere un traditore e a fornire informazioni discordanti ai generali 2 e 3.
Nonostante il problema dei generali bizantini possa sembrare inizialmente di facile soluzione, un semplice calcolo algebrico dimostra che occorrono almeno 3•n+1 generali fedeli per contrastare l'azione prodotta da n traditori. In altre parole, il problema può essere risolto soltanto se almeno due terzi dei generali sono fedeli; un singolo traditore può da solo sabotare l'operato di due generali fedeli. Il problema dei generali bizantini rientra nella classe più generale di problemi in cui occorra trovare un accordo o soluzione comune in un sistema distribuito. Si tratta in altre parole di un problema di consenso, il quale richiede un algoritmo di consenso per la sua risoluzione. L'obiettivo degli algoritmi di consenso (soprattutto se applicati al contesto delle criptovalute) è quello di assicurare l'affidabilità del sistema trovando un accordo sulla validità dei dati tra un certo numero di agenti o processi. Alcuni di questi agenti o processi potrebbero agire secondo una modalità viziata da guasti, malfunzionamenti o persino da gesti malevoli. L'algoritmo di consenso deve pertanto essere tollerante anche verso questo tipo di evenienza: la consistenza dei dati deve essere anteposta a qualunque altro tipo di considerazione.
La Proof of Work (PoW)
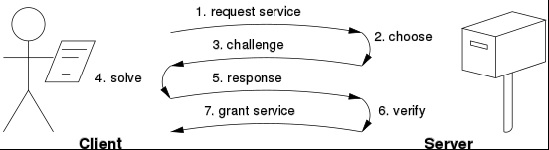
La Proof of Work rappresenta senza ombra di dubbio la prima classe di algoritmi di consenso introdotta nel settore delle criptovalute. Oltre al Bitcoin, l'algoritmo di consenso PoW viene utilizzato su molte criptovalute, tra cui Ethereum, Litecoin, ZCash, Monero e in generale da tutte le monete decentralizzate originate dalla blockchain. Il concetto di PoW è comunque anteriore alla nascita del Bitcoin, essendo stato ipotizzato per la prima volta negli anni '90. Inizialmente questa tecnica venne impiegata per contrastare attacchi informatici di tipo DoS (Denial of Service), spam e ogni altra forma di attacco perpetrato attraverso la rete. La tecnica consisteva nell'obbligare il richiedente di un servizio all'esecuzione di un prova (o calcolo) computazionale, prima di fornirgli il servizio richiesto. L'obiettivo era pertanto quello di scoraggiare gli hacker o comunque evitare un abuso dei servizi disponibili in rete, rendendo questa pratica non più fattibile dal punto di vista dell'efficienza. Al fine di essere efficace, la "prova" doveva avere un livello di complessità sufficientemente alto per chi doveva eseguirla (il richiedente) e nello stesso tempo essere semplice e veloce da verificare (per il fornitore del servizio). Storicamente, uno dei primi sistemi in grado di soddisfare questi requisiti è stato Hashcash, un protocollo PoW sviluppato nel 1997 da Adam Back e basato sull'algoritmo SHA-256. Il principio di funzionamento di questo algoritmo (visualizzato in Figura 3) è molto semplice e si articola sui seguenti passi:
- il richiedente un servizio (client) esegue la richiesta al server
- il server seleziona una proof of work e..
- ..la sottopone al client affinché la risolva
- il client risolve la proof of work e..
- ..invia la risposta al server
- il server verifica che la proof of work sia stata correttamente eseguita
- in caso affermativo, concede al client il servizio richiesto
Nella realtà il numero di PoW sottoposte al client erano molte, dell'ordine di qualche migliaio, ma del resto l'obiettivo principale era quello di limitare gli attacchi DoS e spam alla rete. Per un utente normale questo overhead (stimabile in una frazione di secondo) non rappresenta un grosso problema; viceversa, per un hacker che vuole inviare milioni di messaggi spam in rete rappresenta un ostacolo e un ritardo non trascurabili. La PoW utilizzata dal Bitcoin è simile all'Hashcash, essendo entrambe basate sulla funzione di hash SHA-256. Lo SHA-256 può essere immaginato come una macchina che riceve in ingresso una stringa di caratteri di lunghezza arbitraria e genera in uscita una stringa di lunghezza fissa pari a 256 bit, una sorta di "impronta digitale" associata ai dati in ingresso. Il comportamento della funzione di hash è deterministico: fissato un determinato ingresso, l'uscita corrispondente (hash) sarà sempre la stessa e facilmente verificabile da chiunque utilizzi lo stesso algoritmo. Nel caso del Bitcoin, sappiamo che la PoW viene eseguita dai miner, gli utenti che svolgono il ruolo di validare le transazioni della blockchain, ricevendo in cambio un compenso nella criptovaluta stessa. La PoW viene eseguita dai miner [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2798 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.








La nuova tecnologia delle criptovalute sta facendo passi da giganti ed è veramente difficile aggiornarsi al riguardo. In questo articolo sono stati esposti con estrema semplicità gli algoritmi per la sicurezza nel campo finanziario e alcuni esempi molto significativi. Colpisce subito il problema dei generali bizantini; molti di noi ci saremo posti sicuramente il problema di come si possa concordare un affare a distanza senza avere delle fregature. Adesso, so dare un nome al problema.
Conoscevo già la funzione SHA-256, se non sbaglio, implementabile in PHP; mi ha colpito invece l’algoritmo POS, troppo nuovo per i miei canali di informazione da docente (purtroppo) .
Ho trovato anche molto interessante il DBFT, soprattutto per come è stato illustrato, nei singoli passaggi.
Quali siano i migliori? difficile da dire perchè concettualmente diversi. Le regole della crittografia in generale, avrebbero valutato sicuramente i costi e i tempi per violare un algoritmo.
Ottime info. Un misto tra tecnologia moderna e richiami di storia. Interessante,
Davvero interessante;
avevo letto qualcosa solo sulla PoW, perché legata ad Ethereum e ricordavo in qualche modo come una caratteristica ‘pesante’ l’ingente uso di risorse che richiede; grazie al tuo lavoro apprendo qualcosa in più della più leggera Pos (ma ne avevo sentito parlare) e soprattuto della DBFT, per me assoluta novità.
Saluti.