La diffusione di microcontrollori a basso costo con funzionalità di DSP (Digital Signal Processing) rende disponibili degli apparati in grado di implementare l’elaborazione digitale dei segnali, e in particolare  il filtraggio secondo tecniche digitali. In quest’articolo vedremo un’introduzione alle tipologie di filtri utilizzate in pratica, con particolare riferimento all’implementazione dei filtri passa-basso digitali IIR. Le nozioni di base che saranno esposte sono tuttavia applicabili anche per le altre tipologie di filtri. Per evidenziare un caso pratico d’implementazione infine, saranno esposte brevemente le funzionalità della DSP Library per i DSC delle famiglie dsPIC di Microchip.

Metodologie di filtraggio digitale

Un punto di partenza nella progettazione di un filtro digitale consiste generalmente nella determinazione delle caratteristiche richieste da un filtro analogico corrispondente. Sappiamo che possiamo suddividere le diverse tipologie di filtri in base alla loro risposta in frequenza, distingueremo così tra:

» filtri passa-basso (low pass): riducono tutte le componenti del segnale con frequenze al di sopra di un dato valore;

» filtri passa-alto (high pass): riducono le frequenze al di sotto di un dato valore;

» filtri passa-banda (band pass): riducono le frequenze al di fuori di un certo intervallo;

» filtri elimina-banda (notch): riducono le frequenze comprese in un certo intervallo. Per semplicità, ci riferiremo nel seguito ai soli filtri passa-basso. Le caratteristiche desiderate del filtro sono espresse tramite un insieme di parametri:

» Rp: oscillazione massima (o ripple) in banda passante che possiamo tollerare;

» As: attenuazione minima in banda attenuata che vogliamo ottenere;

» ωp: la pulsazione più elevata della banda passante;

» ωs: la pulsazione dalla quale inizia la banda attenuata.

La banda compresa tra ωp  e ωs è detta banda di transizione. In figura 1 è riportata la risposta in frequenza normalizzata (rispetto al valore a una certa frequenza f0) di un filtro passa-basso.

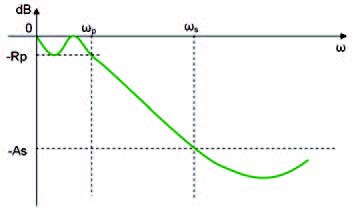
Figura 1: risposta in frequenza normalizzata di un filtro passa-basso.

Le tecniche di filtraggio digitale permettono generalmente di realizzare dei sistemi cosiddetti di tipo LTI (Lineari Tempo Invariante). La risposta di un sistema LTI tempo discreto (cioè campionato) a un qualsiasi segnale in ingresso è determinata dalla sua risposta all’impulso h(n). In effetti le due tipologie di filtri digitali, FIR e IIR, si distinguono per la particolare forma della risposta all’impulso. Vediamo di seguito un confronto qualitativo tra filtri di tipo FIR e IIR.

Filtri FIR (Finite Impulse Response):

» hanno una risposta all’impulso finita (cioè composta da un numero finito di termini) e simmetrica rispetto a un qualche istante di tempo t0;

» permettono di realizzare filtri con risposta di fase lineare, requisito che può essere necessario in alcune tipologie di applicazioni, ad esempio nei sistemi di trasmissione vocale;

» richiedono un maggior numero di coefficienti e quindi un maggiore peso computazionale rispetto ai filtri IIR.

La progettazione dei filtri FIR fa uso di particolari finestre per limitare  il numero di coefficienti della risposta all’impulso, così possiamo trovare diverse metodologie a seconda del tipo di finestra, tra cui Hamming, Hanning, Bartlett (o Triangolare), Rettangolare, Blackman e Kaiser, una delle più efficienti. Tali finestre si distinguono principalmente per avere dei profili di transizione più o meno regolari, così da diminuire le oscillazioni in banda passante e in banda attenuata.

Filtri  IIR (Infinite Impulse  Response):

» presentano un risposta all’impulso infinita;

» la risposta di fase non è lineare, danno quindi luogo a una distorsione di fase;

» hanno dei corrispettivi diretti nei filtri analogici quindi la progettazione può essere più semplice per chi è già esperto nell’utilizzo dei filtri analogici;

» richiedono un minor numero di coefficienti e quindi un minore peso computazionale rispetto ai filtri FIR.

Nel seguito approfondiremo le caratteristiche e la progettazione di un filtro IIR.

Filtri  digitali  IIR: caratteristiche e progettazione

Come accennato, i filtri digitali IIR hanno dei corrispettivi diretti nei filtri analogici, quindi una parte della progettazione consiste nel progettare un filtro analogico che abbia una risposta corrispondente alle specifiche del filtro digitale. Vediamo nello specifico come procedere nel progetto di un filtro digitale IIR. Sebbene esistano numerosi tool software che automatizzano (almeno in parte) questo processo, è sicuramente più utile vedere come procedere, per così dire, manualmente. Potremo così capire meglio come le caratteristiche del filtro si legano agli algoritmi che lo implementano. Il progetto di un filtro IIR passa generalmente attraverso una serie di fasi:

■ 1-determinazione delle specifiche del filtro;

■ 2-traduzione delle stesse nel modello di filtro analogico prescelto;

■ 3-progetto del filtro analogico;

■ 4-conversione del filtro analogico nel tempo discreto;

■ 5-realizzazione  circuitale  (da cui l’algoritmo) del filtro IIR.

Osserviamo innanzitutto come le caratteristiche di un filtro analogico sono espresse tramite la sua risposta in frequenza, o meglio tramite la funzione di trasferimento nel dominio della variabile complessa s. Quindi avremo che la risposta Y(s) al segnale di ingresso X(s) sarà:

dove H(s) è la funzione di trasferimento del filtro. Nella progettazione dei filtri, la funzione di trasferimento è in genere espressa tramite un rapporto di due polinomi:

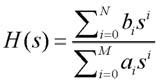
dove N è il numero di zeri della funzione di trasferimento e M il numero di poli. Inutile dire che, affinché  il filtro sia fisicamente realizzabile, deve essere M≥N. Sfruttando la forma precedente di H(s), possiamo esprimere la funzione ingresso uscita del filtro come:

da cui, calcolando l’antitrasformata di Laplace, otterremo la relazione ingresso-uscita nel dominio del tempo, valida nell’ipotesi di condizioni iniziali nulle:

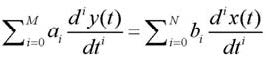
Eq. 1.

Tutto ciò per evidenziare che  lo  scopo ultimo della progettazione del filtro sarà quello di trovare un’approssimazione alle differenze finite (usando, come vedremo, una tra diverse possibili tecniche) nel tempo discreto dell’equazione differenziale su vista.

Fase 1

Supponiamo di avere già disponibili le specifiche del filtro sotto forma dei parametri Rp, As, ωp, ωs, così da passare direttamente  alla fase 2.

Fasi 2 e 3

In queste due fasi eseguiremo la traduzione delle specifiche nel modello di filtro analogico prescelto e il progetto del filtro analogico. Abbiamo visto come le specifiche di un filtro analogico sono fornite in termini dei parametri Rp, As, ωp, ωs.

I modelli  di filtri analogici più utilizzati sono i seguenti:

» Butterworth;

» Chebyshev,  in più varianti;

» Ellittici.

Tali filtri si differenziano tra loro principalmente per l’ordine (vale a dire il numero di poli) necessario per soddisfare  i requisiti, e il ripple in banda passante e in banda attenuata. Riassumendo, possiamo dire che i filtri Ellittici sono quelli che permettono di ottenere la risposta voluta con l’ordine N minore, mentre i Butterworth sono i meno efficienti. Al contrario,  i Butterworth sono filtri a risposta massimamente piatta, mentre gli altri tipi presentano oscillazioni più o meno evidenti. Inoltre, la linearità nella risposta di fase peggiora passando dai Butterworth ai Chebyshev e infine agli Ellittici. Ci riferiamo nel seguito alla progettazione dei filtri Butterworth. I filtri di Butterworth (ovvero  i cosiddetti polinomi di Butterworth) sono caratterizzati dal quadrato del modulo della risposta in frequenza seguente:

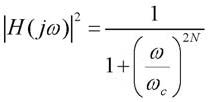
dove ωc è la pulsazione di taglio ricavata dalle specifiche del progetto. La funzione di trasferimento sarà invece:

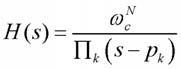
Eq. 2.

dove pk  sono le radici con parte reale <0 (il filtro deve essere stabile!) della funzione di trasferimento:

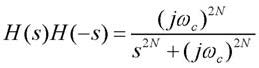
Il progetto del filtro Butterworth richiede innanzitutto di determinare l’ordine N necessario e la pulsazione di taglio ωc  a partire dalle specifiche. Le formule da usare sono le seguenti:

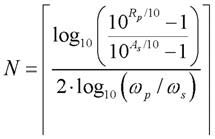
mentre ωc sarà un valore intermedio qualsiasi compreso tra quelli risultanti dai requisiti ωp e ωs, vale a dire tra:

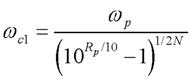
e

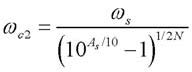
Infine, la funzione di trasferimento sarà ricavata dalla formula dei poli del polinomio di Butterworth [Eq. 2]. Per fortuna esistono delle tabelle che riportano i valori dei polinomi di Butteworth in funzione dell’ordine N, normalizzati rispetto alla pulsazione ωc [1].

Fase 4: passaggio  al tempo  discreto

Così come l’analisi delle funzioni di trasferimento nel tempo continuo è il regno della trasformata di Laplace, nel tempo discreto tale ruolo è svolto dalla trasformata Zeta. Esula dallo scopo di quest’articolo una sia pur breve esposizione della trasformata Zeta, che se necessario potete approfondire su un qualsiasi testo di Metodi Matematici o di elaborazione digitale dei segnali. Una volta progettato il filtro analogico corrispondente alle nostre specifiche, è necessario convertire la funzione di trasferimento nel tempo discreto. Questa conversione è eseguita approssimando l’equazione differenziale [Eq. 1] in modo da ottenere un’equivalente  equazione lineare alle differenze. L’approssimazione può essere eseguita utilizzando diverse tecniche, tra le più comuni ricordiamo la tecnica dell’approssimazione  delle derivate e la tecnica dell’approssimazione  bilineare. Attraverso la tecnica dell’approssimazione delle derivate si approssima l’operazione di derivazione con un rapporto incrementale. Eseguendo quindi la trasformata Zeta dell’approssimazione si ottiene, per confronto con la trasformata di Laplace della derivata, l’equivalenza:

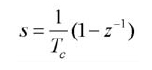
dove Tc  è il  tempo di campionamento che vogliamo utilizzare. Quindi, la funzione di trasferimento nel dominio della variabile complessa z sarà ricavata dalla funzione di trasferimento del filtro analogico ponendo:

Questa tecnica permette di realizzare filtri passa-basso o passa-banda, ma non passa-alto. Altra tecnica comune è quella dell’approssimazione bilineare che approssima il calcolo di un integrale con la formula dei trapezi, valida nel tempo discreto. Analogamente alla tecnica precedente, eseguendo la trasformata Zeta dell’approssimazione si ottiene l’equivalenza:

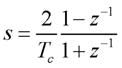
In questo caso la funzione di trasferimento nel dominio di z sarà data da:

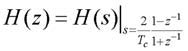
La tecnica bilineare permette di realizzare filtri che non soffrono di aliasing, anche se presentano lo svantaggio di comprimere le frequenza analogiche (il fenomeno è detto warping). Conseguenza di questa compressione è una marcata non linearità di fase per frequenze di ingresso maggiori di 1/(5*Tc).

Fase 5: realizzazione circuitale dei filtri  IIR e algoritmi

L’equazione alle differenze che descrive il comportamento di un filtro IIR è:

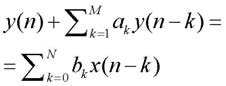
Quindi un filtro IIR è implementato tramite un sistema ricorsivo, vale a dire che l’uscita presente è funzione anche delle uscite passate  (i termini y(n-k). I coefficienti  ak e bk derivano dalle fasi di progettazione del filtro che abbiamo visto in precedenza. Per semplificare la progettazione circuitale dei filtri IIR, conviene lavorare nel dominio di z: la funzione di trasferimento associata all’equazione precedente risulta:

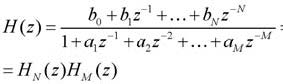
dove HN(z) è la parte non ricorsiva e HM(z) la parte ricorsiva, per chiarezza:

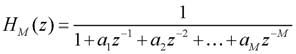
Vediamo finalmente alcune delle realizzazioni circuitali più utilizzate per i filtri IIR, che portano direttamente agli algoritmi per implementarli. Nella realizzazione dei filtri sono impiegati dei blocchi elementari che corrispondono alle operazioni da eseguire, raffigurati in figura 2.

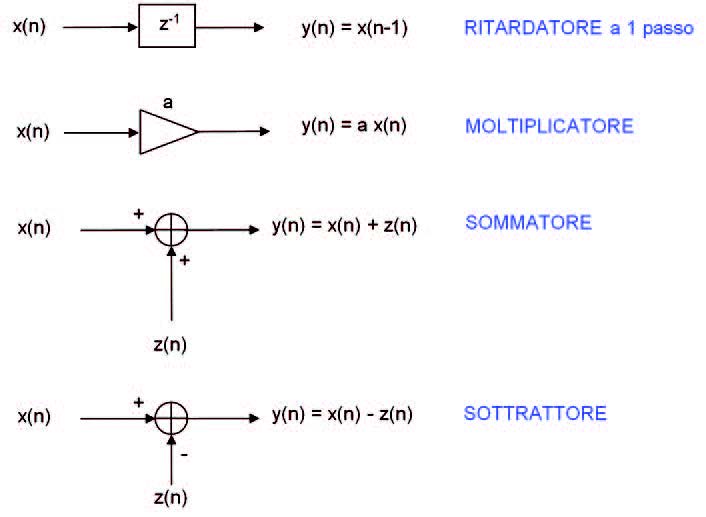
Figura 2: blocchi elementari per la realizzazione dei filtri digitali.

Forma Diretta  I

Lo schema circuitale della forma Diretta  I è rappresentato in figura 3. Osserviamo che il blocco a sinistra rappresenta la parte non ricorsiva HN(z), mentre quello a destra è la parte ricorsiva HM(z).

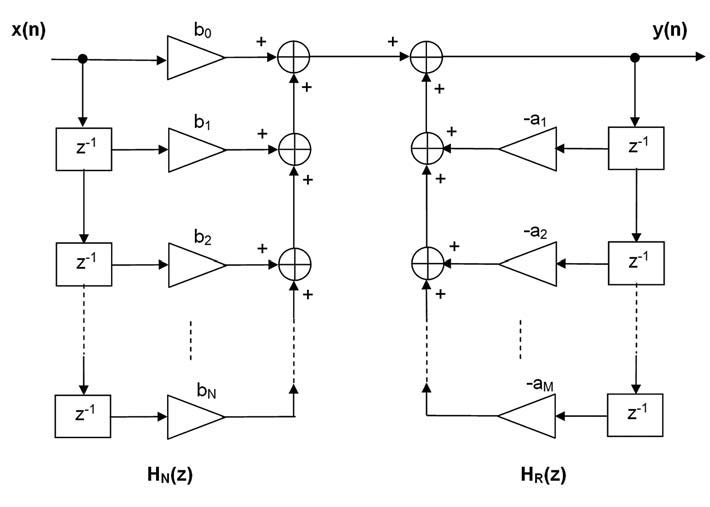
Figura 3: schema di realizzazione di un filtro IIR nella forma Diretta I.

Forma Diretta  II

Questa realizzazione circuitale fa uso delle proprietà della trasformata Zeta per semplificare lo schema, e quindi ottimizzarne le prestazioni. Infatti, invertendo l’ordine di HN(z) e HM(z), si può osservare che entrambi i blocchi usano in ingresso gli stessi ritardatori z(n-k), quindi le loro uscite possono essere riutilizzate. In definitiva si giunge allo schema raffigurato in figura 4.

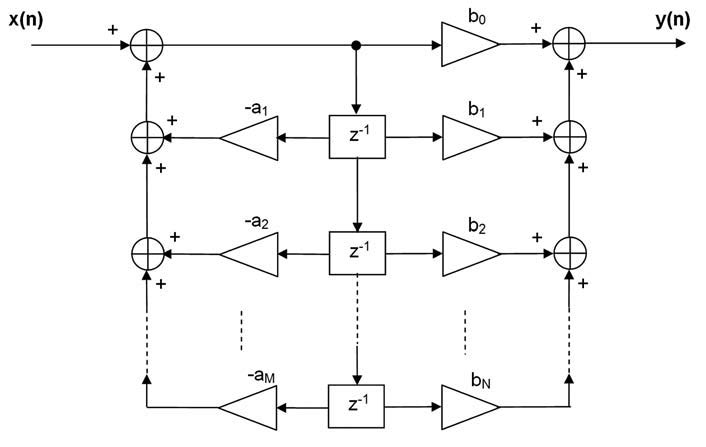
Figura 4: schema di realizzazione di un filtro IIR nella forma Diretta II.

Le forme circuitali dirette che abbiamo visto finora sono in realtà utilizzate raramente, in quanto sensibili agli errori di quantizzazione dei coefficienti. Ciò nonostante sono importanti in quanto utilizzate da altre realizzazioni circuitali come blocchi elementari.

Forma Biquadratica della Diretta  I e II

In questo caso la funzione di trasferimento H(z) viene fattorizzata in q celle elementari, dette biquadratiche:

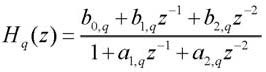
Le singole celle biquadratiche sono realizzate utilizzando una delle forme Dirette che abbiamo visto in precedenza, ad esempio, se utilizziamo la forma Diretta II, lo schema corrisponde a quello in figura 4 per N=M=2. Si noti che le celle elementari di ordine 2 sono ottenute raggruppando coppie di poli e zeri complessi coniugati. Ancora una volta notiamo le analogie con le tecniche di progettazione dei filtri analogici.

Realizzazione  Lattice

Questa realizzazione permette di implementare la parte ricorsiva di un filtro IIR mediante una struttura Lattice, derivata dalla realizzazione dei filtri FIR. Lo schema circuitale di questa configurazione è riportato in figura 5. I  coefficienti sono derivati da quelli della HM(z) in modo automatico dai tool di progettazione. Questo tipo di realizzazione circuitale è particolarmente indicato per applicazioni di trasmissione vocale e altre.

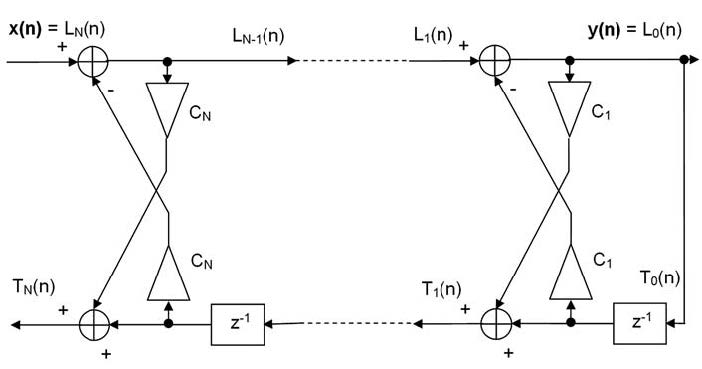
Figura 5: realizzazione Lattice di un filtro IIR.

Un’implementazione pratica: la DSP library per Microchip dsPIC

La DSP Library per i dsPIC di Microchip è una completa libreria di funzioni per l’elaborazione digitale dei segnali sviluppata specificamente per i Digital Signal Controllers delle famiglie dsPIC30F/33F. Come è noto, questi sono dei microcontrollori a 16 bit che includono un engine DSP con moltiplicatore hardware e supporto per l’aritmetica frazionaria. La libreria è ottimizzata per far uso dell’architettura dei dsPIC e del set d’istruzioni assembly dedicate al DSP. È scritta quasi interamente in assembly e comprende delle funzioni C wrapper in modo da poterla utilizzare all’interno di un programma C.

Aritmetica Frazionaria 1.15  e ottimizzazione dei coefficienti

L’implementazione dei filtri IIR e FIR della DSP Library, in particolare, utilizza la cosiddetta aritmetica frazionaria 1.15, un’a ritmetica a virgola fissa dove il bit più significativo è dedicato al segno (1 per numeri negativi) e il punto binario è posto subito dopo. Quindi con questa notazione è possibile rappresentare i  numeri compresi tra -1 e 1-2-15. L’utilità di questa rappresentazione deriva dal fatto che l’operazione di moltiplicazione non è soggetta a overflow, e anche quella di addizione non lo è se la somma è inferiore a 1 in valore assoluto. È inoltre utilizzabile anche in processori che supportano solamente l’aritmetica su interi. Il calcolo dei coefficienti dei filtri è normalmente eseguito tramite un tool specializzato, come Digital Filter Design di Momentum Data Systems. Questo tool è in grado di generare i file header con i coefficienti e altri dati usati dai filtri, utilizzabili direttamente in un progetto MPLAB. I coefficienti  generati  da questi tool sono ottimizzati in funzione delle caratteristiche del DSP da utilizzare: ad esempio nella determinazione dei coefficienti della realizzazione biquadratica di un filtro IIR, le coppie dei poli complessi coniugati devono essere scelte in modo tale da minimizzare la dinamica della singola cella biquadratica. Inoltre, le funzioni della libreria gestiscono l’overflow tramite il metodo della saturazione  (il risultato  è ‘compresso’ tra -1 e 1), per cui non solo i coefficienti dei filtri ma anche i segnali in ingresso vanno ottimizzati (tramite uno studio preliminare) per evitare questa eventualità.  Il metodo utilizzato per la determinazione dell’equazione alle differenze dei filtri IIR è quello dell’approssimazione bilineare, vista in precedenza.

Realizzazione dei filtri  IIR con la DSP Library Vediamo nello specifico quali sono le funzioni fornite da questa libreria per l’implementazione dei filtri IIR. Osserviamo che nell’implementazione dei filtri digitali pratici, è necessario tenere conto non solo delle condizioni iniziali (generalmente nulle) ma anche della storia del filtro su un certo numero di campioni precedenti. Infatti un filtro reale opera sempre su un numero finito di campioni, mentre le sue uscite costituiranno a loro volta lo stato d’ingresso dell’operazione di filtraggio successiva. Questi valori costituiscono la cosiddetta delay line del filtro.

Forma Biquadratica  Canonica

La funzione IIRCanonic() utilizza una cascata di celle biquadratiche, ognuna delle quali è implementata con una forma Diretta II di filtro IIR. I coefficienti  del filtro, la delay line e altri parametri sono passati tramite la struttura:

typedef struct {
int numSectionsLess1;
fractional* coeffsBase;
int coeffsPage;
fractional* delayBase;
int initialGain;
int finalShift;
} IIRCanonicStruct;

mentre il prototipo della funzione IIRCanonic() è il seguente:

extern fractional* IIRCanonic (
int numSamps,
fractional* dstSamps,
fractional* srcSamps,
IIRCanonicStruct* filter
);

dove numSamps è il numero di campioni N su cui opererà il filtro, dstSamps è un puntatore ai valori y in uscita e srcSamps un puntatore ai campioni x in ingresso. Il filtro va sempre inizializzato  tramite la funzione:

extern void IIRCanonicInit (
IIRCanonicStruct* filter
);

la quale si occupa di inizializzare a zero la delay line. La complessità computazionale minima di questo filtro è pari a 36 + N(8 + 7S), dove N è il numero di campioni e S il numero di celle biquadratiche del filtro.

Forma Biquadratica  Trasposta

La funzione IIRTransposed() utilizza una cascata di celle biquadratiche ognuna delle quali è implementata con una forma Diretta II Trasposta  di filtro IIR. I coefficienti del filtro, la delay line e altri parametri sono passati tramite la struttura:

typedef struct {
int numSectionsLess1;
fractional* coeffsBase;
int coeffsPage;
fractional* delayBase1;
fractional* delayBase2;
int finalShift;
} IIRTransposedStruct;

Notiamo che la delay line usa in questo caso due buffer separati.  Il prototipo della funzione IIRTransposed() è il seguente:

extern fractional* IIRTransposed
(
int numSamps,
fractional* dstSamps,
fractional* srcSamps,
IIRTransposedStruct* filter
);

anche in questo caso, numSamps è il numero di campioni N su cui opererà  il filtro, dstSamps è un puntatore ai valori y in uscita e srcSamps un puntatore ai campioni x in ingresso.  Il filtro andrà sempre inizializzato tramite la funzione:

extern void IIRTransposedInit (
IIRTransposedStruct* filter
);

La complessità computazionale minima di questo filtro è pari a 35 + N(11 + 11S), dove N è il numero di campioni ed S il numero di celle biquadratiche del filtro.

Realizzazione  Lattice

La realizzazione Lattice di un filtro IIR è implementata dalla funzione IIRLattice(). L’ordine order del filtro, i coefficienti  dello stesso (kappaVals  e gammaVals), la delay line e altri parametri sono passati tramite la struttura:

typedef struct {
int order;
fractional* kappaVals;
fractional* gammaVals;
int coeffsPage;
fractional* delay;
} IIRLatticeStruct

mentre il prototipo della funzione IIRLattice() è il seguente:

extern fractional* IIRLattice (
int numSamps,
fractional* dstSamps,
fractional* srcSamps,
IIRLatticeStruct* filter
);

Come negli altri casi, il filtro va sempre inizializzato tramite la funzione:

extern void IIRLatticeInit (
IIRLatticeStruct* filter
);

La complessità computazionale minima di questo filtro è pari a 46 + N(16 + 7M), mentre, nel caso di un filtro con soli poli, è 46 + N(16 + 6M), dove N è il numero  di campioni ed M è l’ordine del filtro (è sempre N≥M).

Conclusioni

L’esposizione fatta nel corso di questo articolo va intesa come una prima introduzione al vastissimo settore del filtraggio digitale. Dovrebbe comunque essere sufficiente per poter utilizzare i tool e le librerie esistenti per lo sviluppo e l’implementazione di filtri IIR e FIR con un minimo di cognizione di causa.

Ti potrebbe interessare anche:

Micro a 8 bit o ARM?

Aumentare la performance LED strip – Puntata 1

Il talk sull’Energy Harvesting al Campus Party @ Milano