
In quest’articolo verrà illustrato come migliorare l’accuratezza della misura di inclinazione usando un accelerometro combinato con un giroscopio. Tanto sulle strade in pendenza quanto su quelle in pianura, per mantenere fermi i veicoli ad uso privato si utilizzano spesso i freni di parcheggio (EPB) elettrici. Il loro intervento si ottiene misurando l’inclinazione tramite un accelerometro a singolo o doppio asse. Tipicamente, un accelerometro x-, y-, o -z a basso-g viene collocato in un modulo dedicato EPB. Attualmente, sono sempre più numerosi i veicoli dotati della funzione di controllo elettronico della stabilità (ESC), ottenuta con un accelerometro a basso-g e un giroscopio combinati in un singolo chip. Questa implementazione è stata introdotta per prevenire lo sbandamento laterale e il ribaltamento del veicolo; oggi la funzionalità ESC è richiesta per Legge in tutto il mondo per i nuovi veicoli.
Introduzione
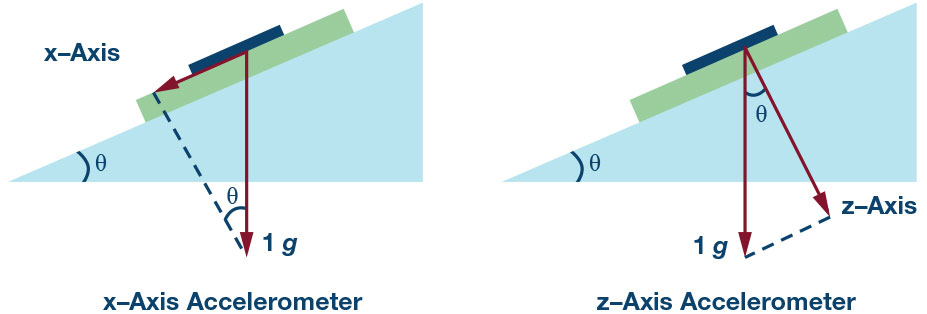
Se la misura di inclinazione venisse realizzata mediante un singolo chip con giroscopio e accelerometro combinati, non sarebbe più necessario disporre di un modulo autonomo EPB a bordo del veicolo, contribuendo significativamente alla riduzione del costo della vettura. Essendo tipicamente destinato all’ESC, un componente combinato non è ottimizzato per rilevare l’inclinazione e, talvolta, la sua accuratezza in questo tipo di misure non soddisfa le specifiche richieste. Essendo configurato sugli assi xy o xyz, per la misura dell’inclinazione utilizza solitamente l’asse x e alcuni accelerometri tradizionali a basso-g nei moduli EPB usano l’asse z, perché sono installati verticalmente nel vano motore. Per ottenere un’accuratezza migliore, l’asse di rilevamento dovrebbe essere collocato perpendicolarmente rispetto a quello gravitazionale ma di questo discuteremo più avanti.
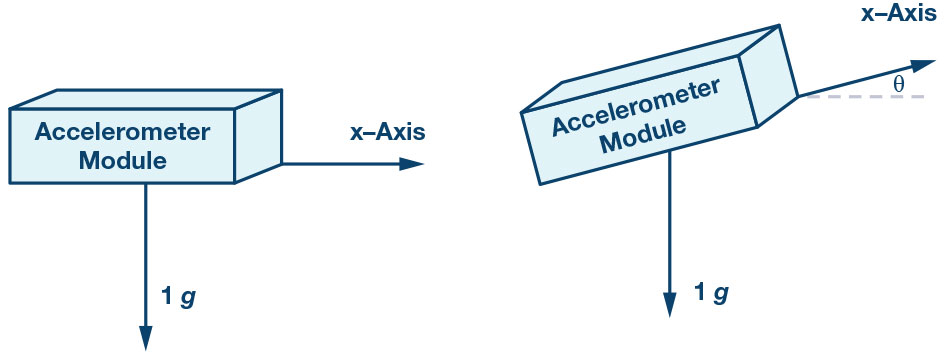
Per la misura dell’inclinazione di un veicolo è molto importante valutarne l’accuratezza. Immaginate che la vostra vettura sia parcheggiata su una superficie assolutamente orizzontale, in tal caso l’angolo calcolato dall’accelerometro dovrebbe essere 0°. Se invece fosse parcheggiata su una rampa, l’inclinazione dovrebbe essere rilevata accuratamente, in modo tale da poter attivare correttamente l’impianto frenante.
Per cui
Dove:
AOUT rappresenta l’uscita dell’accelerometro espressa in g.
θ rappresenta l’inclinazione della rampa espressa in gradi.
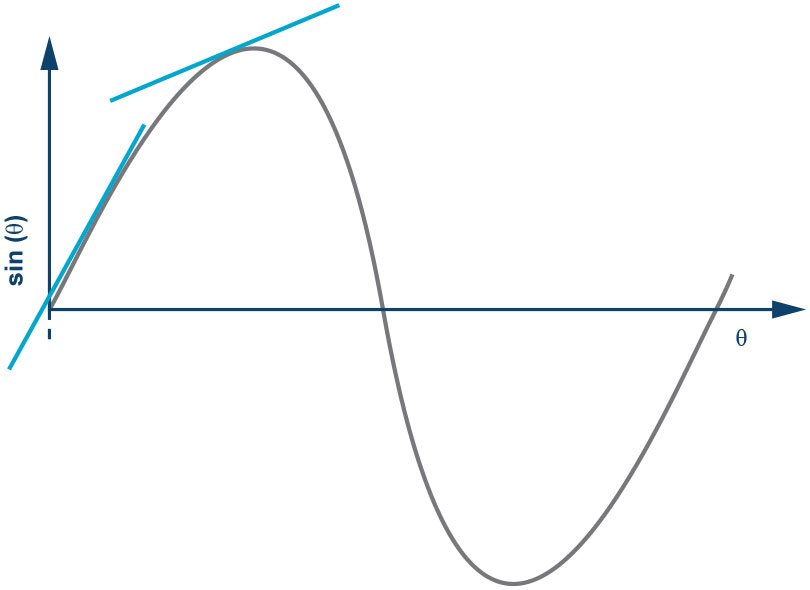
Dato che il seno di θ e’ una funzione non-lineare, cosi sara’ il rapporto tra AOUT e θ e presentera’ la miglior linearità, ovvero dispone della migliore accuratezza di misura, intorno allo zero. All’aumentare di θ, l’accuratezza, questo spiega perché l’asse di rilevamento debba essere collocato perpendicolarmente a quello di gravità, in quanto l’angolo di pendenza stradale sarà prossimo allo zero.
Per la misura dell’inclinazione in un veicolo, non è necessario che il sistema consideri l’intervallo completo della pendenza. Nel mondo reale, nella maggior parte dei casi la pendenza stradale non dovrebbe superare i 30°. Sarà quindi sufficiente analizzare l’accuratezza dei contributi nell’intervallo di ±30°.
Ci sono diversi fattori in grado di condizionare l’accuratezza della misura:
- Errore di sensibilità e offset iniziale assoluto
- Non-linearità
- Variazione complessiva dell’offset rispetto all’offset iniziale assoluto
- Rumore
Errore di sensibilità e offset iniziale assoluto
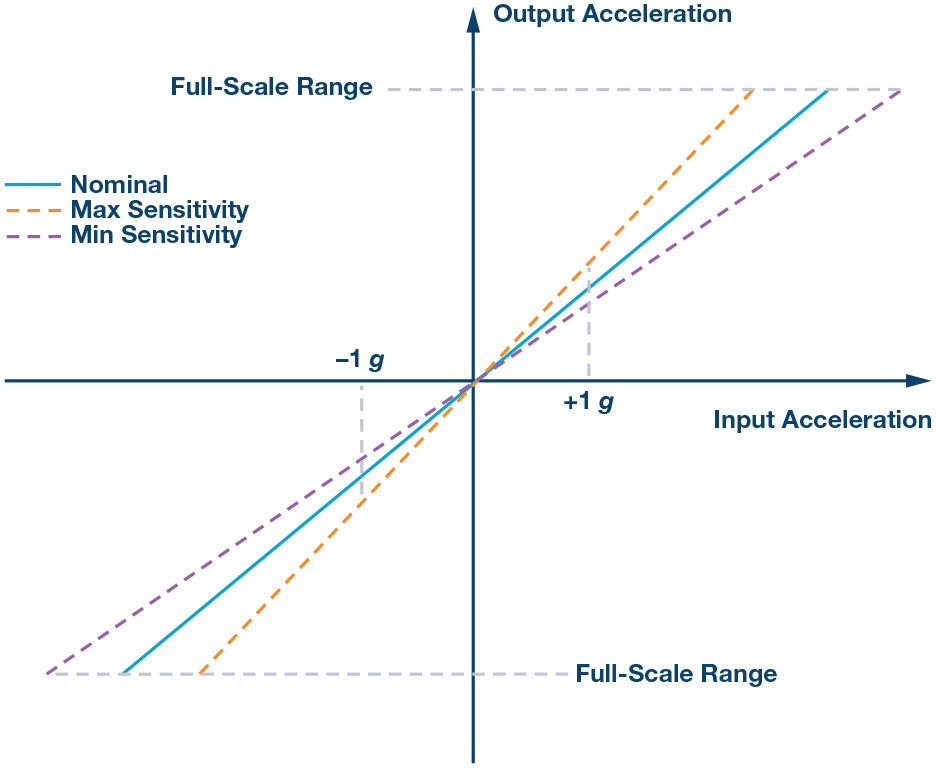
Errore di sensibilità
La sensibilità è la pendenza della funzione di trasferimento misurata tra ingressi e uscite, solitamente a +1 g e –1 g. L’errore di sensibilità è la deviazione della medesima da parte a parte. Per esempio, la massima sensibilità di alcuni accelerometri è del 3%.
Offset iniziale assoluto
L’offset entro l’intervallo è considerato nell’intorno dei 25°C; per esempio, 25°C ± 5°C, misurati immediatamente al termine della realizzazione del modulo. L’offset iniziale assoluto denota la deviazione standard dei valori di offset, misurati su un numero elevato di dispositivi.
Calibrazione a due punti
Per le applicazioni di misura dell’inclinazione, le due principali fonti di errore riguardano offset e sensibilità. Questi due errori portano a risultati di rilevamento inaccettabili, per cui non possono essere trascurati; se vogliamo rimuovere queste due componenti, è necessario calibrare l’uscita relativa all’accelerazione. Genericamente, c’è una calibrazione unica per offset e sensibilità della misura d’inclinazione: se si considera l’errore di offset e sensibilità, il rapporto tra ingresso e uscita dell’accelerometro è:
Dove:
AOUTPUT rappresenta l’errore di offset espresso in g.
Gain rappresenta il guadagno dell’accelerometro, il valore ideale è 1.
AACTUAL è l’accelerazione reale applicata all’accelerometro, espressa in g.
Esistono solo due semplici tecniche di calibrazione: una è quella a singolo-punto, che si esegue applicando sull’accelerometro un campo a 0 g, per poi misurarne l’uscita. Questo tipo di operazione potrebbe essere usato solo per la calibrazione dell’errore di offset mentre l’errore di guadagno non verrebbe calibrato. In seguito, per rimuovere l’errore di offset, l’uscita risultante da un campo a 0 g viene sottratta dal valore reale d’uscita; metodo semplice per eseguire la calibrazione ma non vale per l’accuratezza, poiché esiste ancora un errore di sensibilità. Un altro metodo consiste nella calibrazione con un salto di 1 g, che dovrebbe usare una calibrazione a due punti a +1 g e –1 g; per i valori a +1 g e –1 g si misura l’uscita di accelerazione:
Dove l’offset, AOFFSET, è espresso in g.
Da questa informazione a due punti, offset e gain si potrebbero risolvere nel modo seguente:
Dove le misure +1 g e −1 g, A+1 g e A–1 g sono espresse in g.
Dopo questa calibrazione unica, l’effettiva accelerazione si potrebbe calcolare secondo l’equazione seguente, eliminando di volta in volta l’errore relativo a offset e sensibilità.
Dove AOFFSET e AOUT sono espressi in g.
Non-linearità
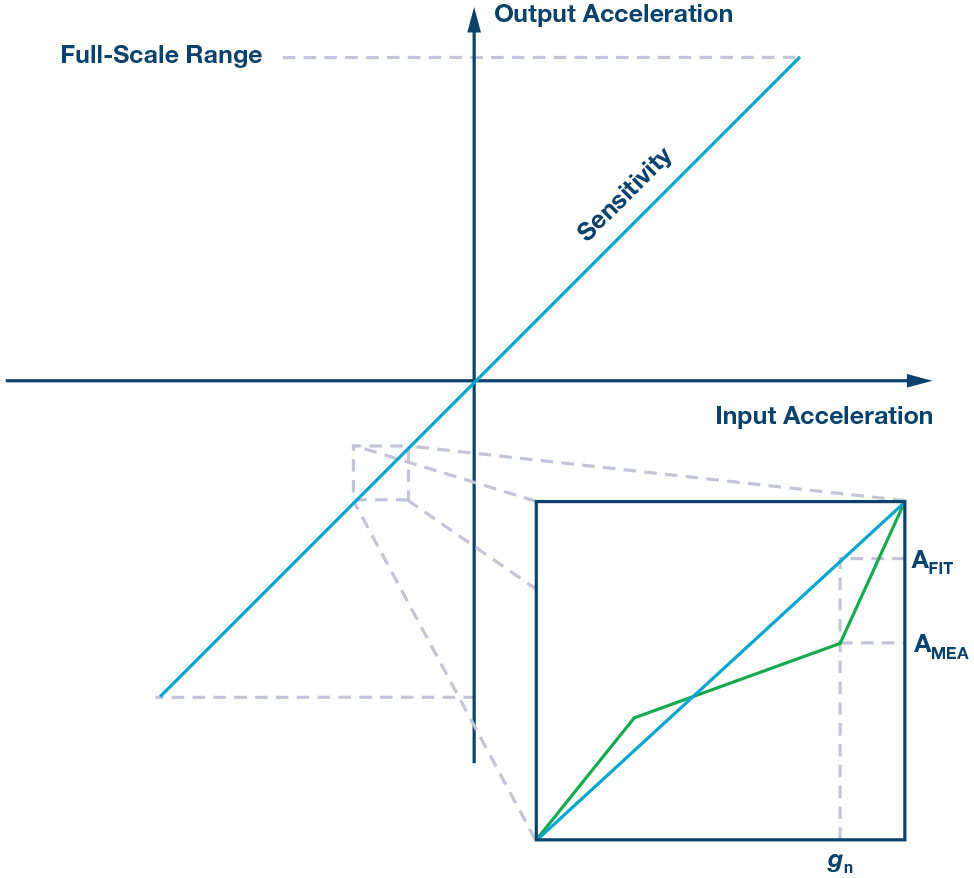
La non-linearità del dispositivo è rappresentata dalla massima deviazione dell’accelerazione misurata (AMEA) e dell’accelerazione lineare ideale d’uscita (AFIT). L’insieme dei dati della misura di accelerazione dovrebbe includere l’intervallo di fondo scala dell’accelerometro, che viene misurato come Max(|AMEA – AFIT|).
Dove:
AMEA è l’accelerazione misurata a un determinato valore di gn.
AFIT è l’accelerazione prevista a un determinato valore di gn.
La maggior parte degli accelerometri o dei componenti combinati soffrono di non-linearità su un dato intervallo d’ingresso, per esempio di 2g ± 30 mg. Per le applicazioni di misura dell’inclinazione, la pendenza della rampa di ingresso è nell’intorno di ±30°, cioè l’intervallo d’accelerazione d’uscita si trova entro ±500 mg (±1 g × sen 30°), per cui la non-linearità in questo intervallo dovrebbe essere verificata nuovamente. Dal momento in cui la non-linearità si verifica attraverso l’intero intervallo di ingresso, è difficile valutare quantitativamente e in modo accurato questa componente dell’errore. Tuttavia, poiché le specifiche tecniche su questo aspetto sono sempre piuttosto prudenti, per una non-linearità di 30 mg con un intervallo di ingresso di ±2 g, si potrebbe ragionevolmente considerare un errore di calcolo di 10 mg con un ingresso entro i ±500 mg.
Variazione di offset complessiva rispetto all’offset iniziale assoluto
La variazione complessiva dell’offset rispetto all’offset iniziale assoluto è la deviazione massima dell’offset per come viene indotta da temperatura, stress e invecchiamento. Questa deviazione viene misurata relativamente all’offset iniziale assoluto per un dato dispositivo e costituisce il fattore più rilevante all’errore complessivo di accuratezza.
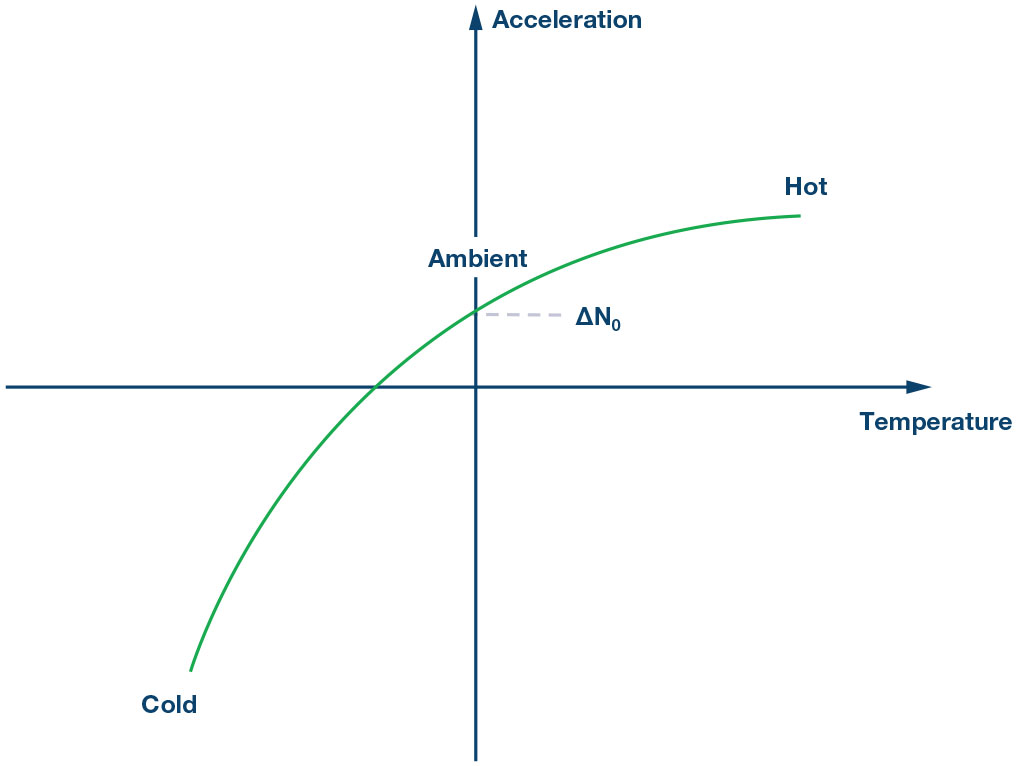
Tra tutti gli elementi, quali temperatura, stress, invecchiamento, etc., la variazione sulla temperatura è la maggiore responsabile della variazione complessiva dell’offset . Genericamente, quella relativa alla variazione su temperatura è una curva di second’ordine, nello specifico una parabola ruotata. Per eliminare questa componente d’errore, si deve eseguire una calibrazione a tre punti a livello di sistema. Per un dato dispositivo, lo scostamento del valore d’uscita dovuto a temperatura si potrebbe calibrare secondo i passi seguenti.
Passo 1:
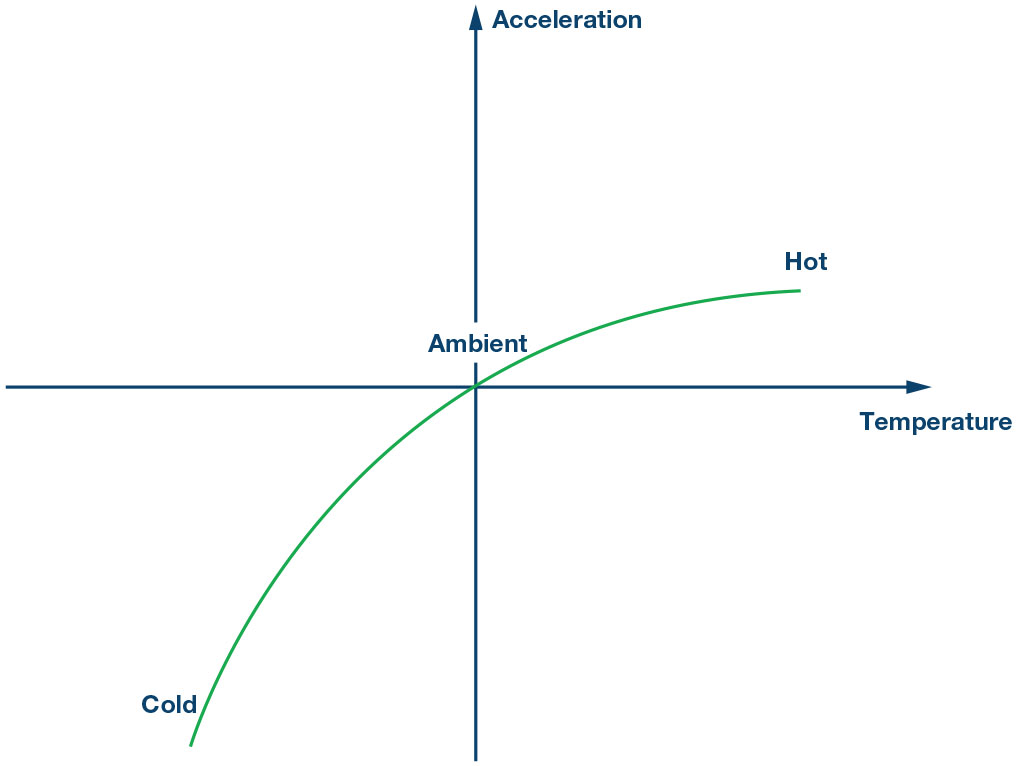
La risposta d’uscita del dispositivo è traslata di un valore ΔN0. Il primo passo nel processo di calibrazione su temperatura consiste nell’eliminazione dell’offset a temperatura ambiente.
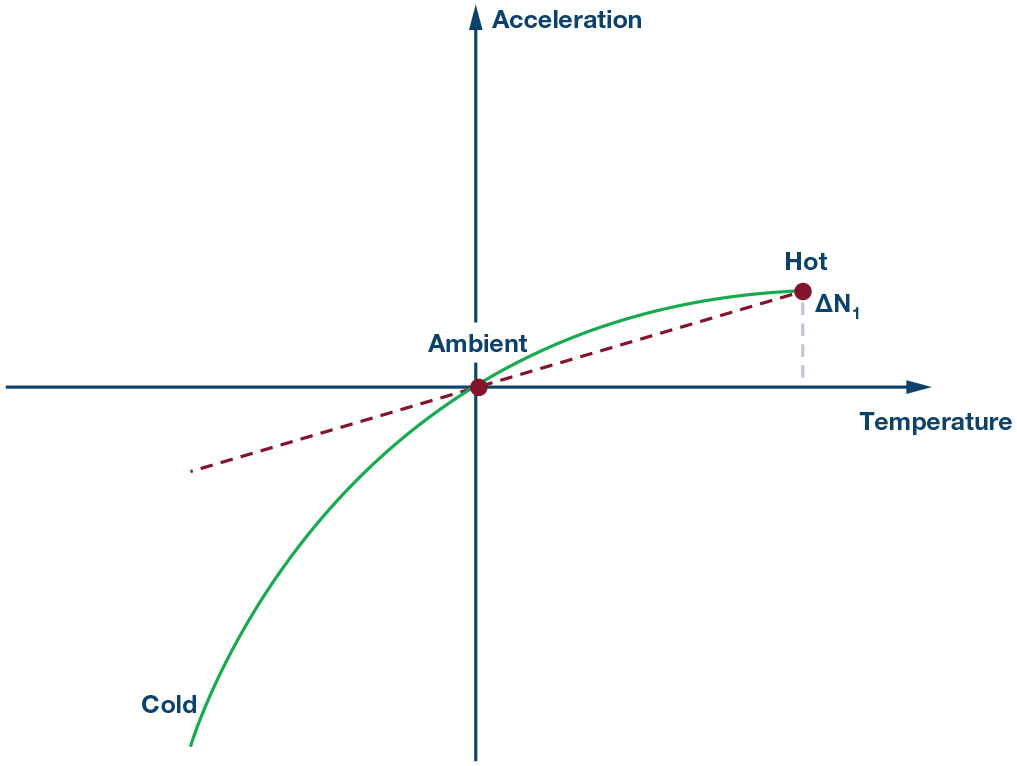
Passo 2:
In seguito, il dispositivo viene collaudato a caldo e questa nuova informazione viene utilizzata per generare un’equazione lineare per la correzione dell’offset.
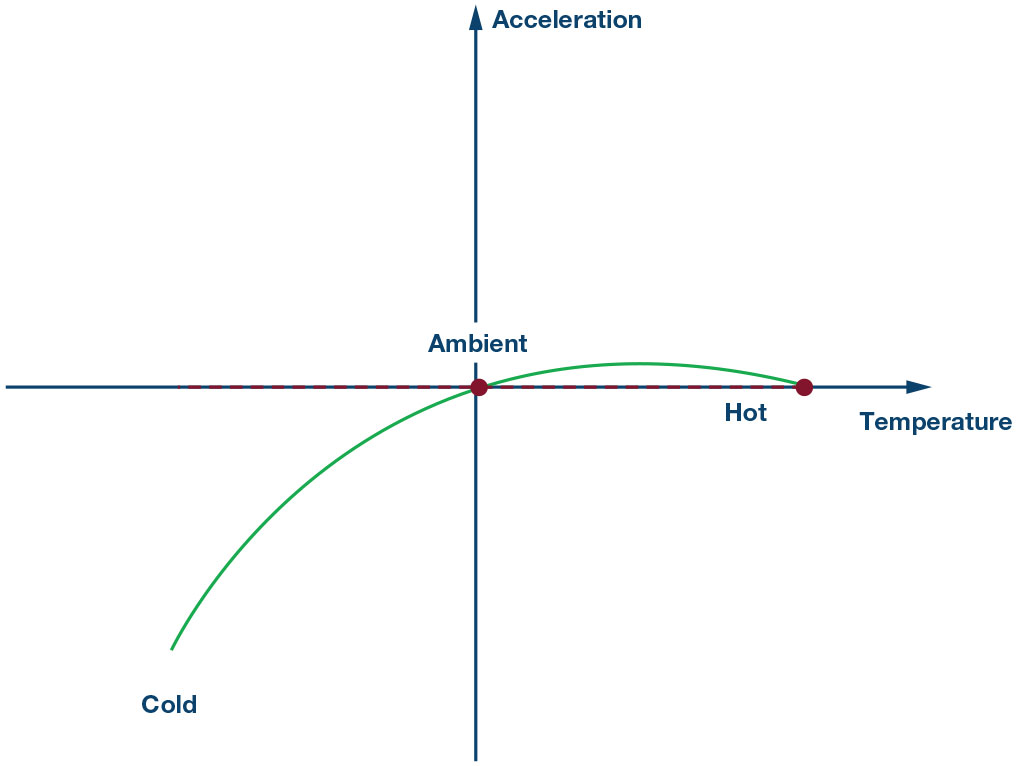
Figura 9. Passo 4: la curva dopo l’eliminazione della componente di rotazione a caldo della parabola.
Passo 3:
Per correggere la parte rimanente dell’offset, all’equazione esistente viene aggiunto un componente di second’ordine. Supponendo che la curva di second’ordine segua l’equazione:
Questa è la formula relativa a una parabola di second’ordine e la componente rotatoria è stata eliminata attraverso i passi 1 e 2.
Questa parabola di second’ordine offre tre soluzioni all’equazione:
Quindi possiamo ricavare tempco a, b, c.

Figura 10. Passo 5: aggiunta di un componente di secondo ordine per l’eliminazione dell’offset residuo.
Tutta l’informazione tempco di ΔN0, ΔN1, ΔN2, a, b, c dovrebbe essere conservata nella memoria non-volatile del sistema ed e’ quindi necessario avere nel sistema un sensore di temperatura. Il sistema dovrebbe calibrare l’accelerometro in modo routinario dopo ogni accensione, per garantire l’eliminazione della variante scostamento su temperatura.
Rumore
Una misura di inclinazione basata su un singolo campione di dati potrebbe non essere affidabile. Anche se l’accelerometro avesse un rumore pari a zero, le misure di inclinazione avvengono col veicolo in funzione, per cui tutte le vibrazioni causate dal motore, da altri veicoli o dallo spostamento dei passeggeri nell’abitacolo, dovranno essere attenuate. Il modo migliore per farlo è mediare i dati il più a lungo possibile senza scendere al di sotto dei requisiti minimi della velocità di trasferimento. Questa mediazione ridurrà il rumore rms.
Supponendo di campionare il rumore, otteniamo una varianza per-campione di
La media di una variabile casuale porta alla varianza seguente,
Dato che, a σ2, la varianza del rumore è costante
Dimostrando che la media di n realizzazioni del rumore non-correlato riduce la potenza di rumore per un fattore n, e il rumore rms verrebbe ridotto in ragione di √n.
Essendo il rumore casuale soggetto alla distribuzione Gaussiana, il rumore rms è equivalente alla deviazione standard della distribuzione Gaussiana stessa. La popolazione minima entro 6σ è 97%.
Per esempio, se mediate ogni 100 ms di dati a 1 kSPS, si ha un rumore massimo rms = 0,4 mg, significa che il calcolo del rumore di picco a quel punto è soltanto 2,4 mg, usando 6σ come distanza dal valor medio.
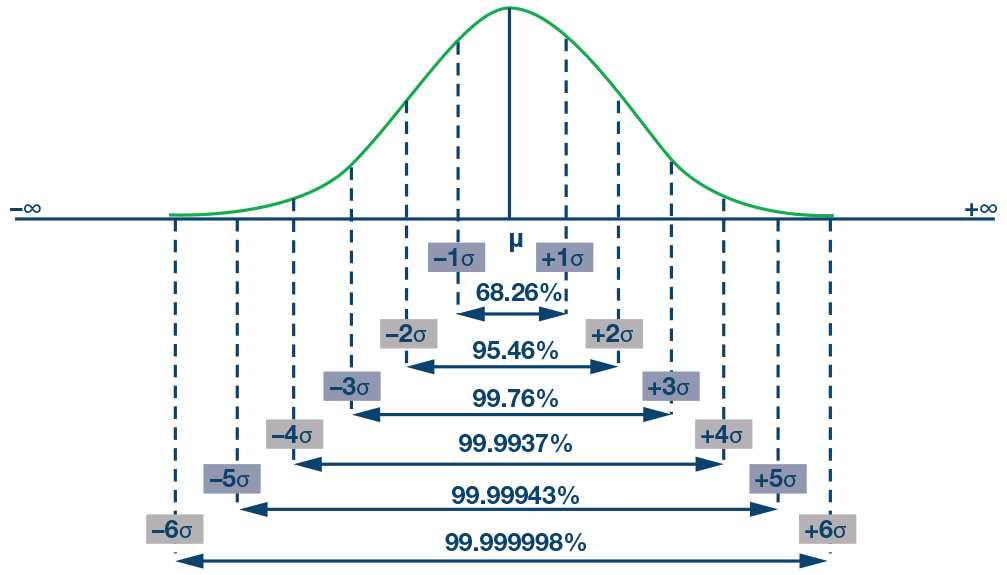
I fattori per i quali moltiplicare il valore rms dipendono dalle esigenze statistiche del profilo di missione. Ad esempio, la scelta di 6 come fattore (il rumore picco-picco è 6 × rumore rms) avrà un impatto sulla probabilità che si verifichi lo scenario di worst case durante il ciclo di vita del componente. Il rumore RMS è un valore fisso indicato nelle specifiche del prodotto, ed è la deviazione standard, che si trova nella distribuzione di 1 sigma. Non può essere usato per i calcoli, perché il limite di contenimento entro la distribuzione 1 sigma è soltanto il 68,26%. Questo spiega perché dobbiamo scegliere un fattore più alto con il quale moltiplicare il rumore rms, che porterà a un contenimento migliore.
Teoricamente, il fattore che moltiplica il rumore rms determinerà l’incidenza dei guasti durante il ciclo di vita dell’algoritmo, perché il rumore è una variabile casuale nel tempo, che può essere stimato statisticamente.
Supponiamo che l’algoritmo di un modulo EPB abbia un’aspettativa di vita di 146.000 (cioè 20 volte al giorno per 20 anni). Se nel suo ciclo di vita non sono consentiti guasti, la massima probabilità che si verifichi un guasto è 1/146.000 = 0,00068%.
Secondo il livello del sigma della distribuzione Gaussiana (Figura 11), un valore di 6 genera una percentuale di difetto di 0,00034%. Perciò, scegliendo 6 come il fattore di moltiplicazione rms corrisponde a 146.000 × 0,00034% = 0,5 < 1.
Questo significa che statisticamente per il modulo EPB non si verificheranno guasti in un periodo di vita utile di 20 anni.
Possiamo riassumere il tutto come:
E è il numero di eventi che eccedono il worst case durante il ciclo di vita, M le attivazioni durante il ciclo di vita e r la probabilità di eccedere il worst case. Basandoci su questo, possiamo valutare un fattore ragionevole per moltiplicare il rumore rms.
Riepilogo
Prendendo come esempio l’ADXC1500/ADXC1501 di ADI (un giroscopio e un accelerometro a 2-assi/3-assi combinati), nella Tabella 1 vengono elencati i parametri che contribuiscono all’errore, con e senza misure di calibrazione. Possiamo partire dal presupposto che la variazione complessiva dell’offset sia la seconda curva e la variazione su temperatura rappresenti l’80% della sua variazione di offset totale. Inoltre, possiamo considerare 6 come fattore moltiplicativo per il massimo valore del rumore rms.
Questa combinazione di giroscopio e accelerometro triassiale permette la realizzazione di molteplici nuove applicazioni, specialmente nei sistemi di sicurezza per automotive e nel campo dell’automazione industriale. Ridurre al minimo l’insorgere di errori elevati è un aspetto fondamentale nella missione di progetto di sistemi di sicurezza per automotive accurati e affidabili, come il controllo elettronico della stabilità (ESC) e il rilevatore di ribaltamento. Questi sistemi vanno ad aggiungersi a quelli di controllo del telaio, già tradizionalmente presenti nel veicolo, inclusi quelli di prevenzione del blocco dei freni, di controllo della trazione e dell’imbardata.
Tabella 1. Contributi di errore con/senza calibrazione
| Contributo di errore | Prima della calibrazione | Dopo la calibrazione | Misura della calibrazione |
| Errore di sensibilità | 30 mg | 0 mg | Calibrazione a due punti |
| Offset iniziale assoluto | 15 mg | 0 mg | Calibrazione a due punti |
| Non-linearità | 10 mg su ±500 mg | 10 mg su ±500 mg | Nessuna |
| Variazione di offset complessiva | 50 mg | 10 mg | Calibrazione a tre punti |
| Rumore | 24 mg | 2,4 mg | Calcolo del valor medio 100× |
| Errore complessivo | 129 mg | 22.4 mg | |
| Accuratezza | 7,4° (caso peggiore) | 1,28° (caso peggiore) | In gradi |
A cura di Allen Fan


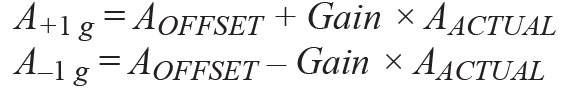
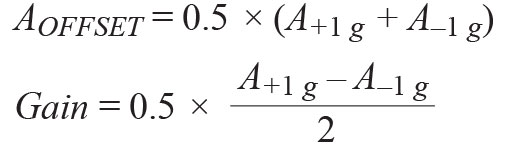

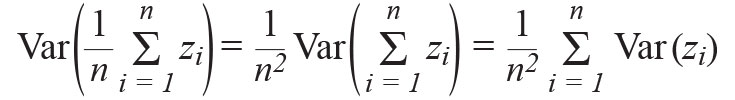





E’ un dato di fatto, ormai: qualsiasi strumento è elettronico. Bilance, metri, goniometri, nonio, ecc ecc sono tutti elettronici. E con la precisione dell’elettronica.
La sicurezza e la precisione nelle applicazioni automotive e in quelle di industrial automation sono determinanti per la buona riuscita del funzionamento del sistema. Controllo elettronico della stabilità, rilevatore di ribaltamento sono alla base di un sistema affidabile e sicuro. Sostanzialmente nella progettazione l’obiettivo è quello di ottenere un sistema affidabile, ammettendo il massimo errore consentito (minimo costo) che non pregiudichi le funzionalità e che garantisca la riuscita.