
I problemi statistici inversi sorgono quando c'è la necessità di inferire i parametri di un modello matematico a partire dai dati osservabili disponibili. Il problema diretto, invece, si ha nel caso in cui si devono inferire dati osservabili a partire dai parametri di un modello, ma quando si ha a che fare con grandi volumi di dati questo procedimento non è più possibile. In questo articolo tratterò di uno di questi problemi statistici inversi, il problema inverso di Ising, e mostrerò le sue applicazioni in ambiti tra loro apparentemente lontani quali la determinazione della forma tridimensionale delle proteine, la ricostruzione di interazioni neurali e le reti di regolazione genetica.
Introduzione
La fisica statistica ha l'obbiettivo principale di derivare quantità osservabili da leggi che regolano le entità che costituiscono un sistema. In particolare, il problema di Ising è quello di derivare da un modello che descrive le possibili interazioni tra magneti elementari, chiamati spin, le magnetizzazioni e le interazioni osservabili tra magneti in un dato caso. Nei problemi inversi la base di partenza è l'osservazione del comportamento e delle caratteristiche delle entità che compongono un sistema mentre i parametri del modello che si vuole descriva il sistema sono del tutto sconosciuti. Nel problema inverso di Ising devono essere misurate il valore dei campi magnetici a cui sono soggetti gli spin e le interazioni tra i magneti insieme ad altri fenomeni osservabili per poi inferire i parametri di un modello, come ad esempio la funzione Hamiltoniana del sistema.
La necessità di risolvere problemi statistici inversi è nata da una parte dalla grande abbondanza di dati provenienti da fenomeni di piccolissima scala, dall'altra dalla possibilità data dalle nuove tecnologie di immagazzinare e processare grandi volumi di dati. Il campo di ricerca aperto dalle nuove tecnologie, chiamato "big data", è dunque legato a doppio filo con i problemi statistici inversi. Senza la possibilità di immagazzinare e processare grandi volumi di dati, i metodi di statistica inversa non sarebbero attuabili mentre, senza tali metodi, l'immagazzinamento di dati sarebbe di per sé infruttuoso.
In biologia, i problemi statistici inversi legati al problema inverso di Ising, dei quali parleremo più estesamente in seguito, coinvolgono ricerche che vogliono derivare la costruzione di reti neurali a partire dai dati osservabili di popolazioni di neuroni, la formazione di reti di geni regolatori, la determinazione della struttura tridimensionale delle proteine.
In fisica i problemi statistici inversi riguardano la configurazione di sistemi composti da molti corpi a partire da particolari proprietà desiderate. Un esempio di questo tipo di problemi inversi è la ricerca di come devono essere i potenziali dato un determinato reticolo cristallino di atomi.
Nel campo di studio del machine learning, invece, si cerca di istruire le reti neurali artificiali al fine di produrre statistiche il più possibile vicine ad un insieme prestabilito di dati.
Applicazioni del problema inverso di Ising
Specifichiamo ora il problema inverso di Ising. Se prendiamo in esame un sistema ad N variabili binarie che hanno come valori gli spin di Ising che possono variare discretamente tra ± 1, che interagiscono a coppie e sono soggette a campi magnetici esterni, possiamo considerare la seguente formula:
L'equazione ci dice che la distribuzione di probabilità che il sistema sia in uno stato specifico di spin è uguale ad 1 fratto un fattore Z chiamato fattore di Boltzmann, nient'altro che una funzione di partizione utile a fare in modo che la somma delle probabilità che il sistema assuma gli stati particolari di spin sia uguale a 1, per la costante e elevata alla somma della sommatoria dei prodotti tra il valore degli spin e dei relativi campi magnetici e la sommatoria delle interazioni magnetiche tra due spin per il prodotto dei loro valori, interazione dovuta all'interazione dei loro momenti magnetici.
L'Hamiltoniana della funzione precedente può essere espressa così:
questa funzione specifica l'energia del sistema che varia in funzione di quelli che abbiamo visto essere i valori di spin, i campi magnetici locali, e le interazioni magnetiche.
Se il problema di Ising è determinare il valore delle configurazioni sperimentali di spin a partire da interazioni magnetiche e campi magnetici conosciuti, il problema inverso è quello di determinare valori per i campi magnetici e per le interazioni una volta che sono conosciuti i valori di un certo numero di configurazioni di spin e le loro variazioni statistiche.
Dai pattern di scarica alle interazioni neurali
I neuroni comunicano tra di loro attraverso scariche elettriche discrete che viaggiano lungo le fibre nervose e sono tali da poter essere semplicemente descritti come neuroni in scarica o neuroni silenti e quindi paragonabili agli spin di Ising . La misurazione di queste scariche avviene attraverso registrazione multipla a singoli neuroni e dà agli sperimentatori la possibilità di ricostruire il funzionamento di alcune aree cerebrali per compiti cognitivi elementari una volta che siano conosciuti i pattern di scarica di una popolazione di cellule neurali sufficientemente grande. Anche se i dati disponibili sono in grande quantità, difficilmente il numero delle diverse configurazione del nostro sistema di rete neurale sarà sufficientemente grande da essere paragonabile alla totalità di tutte le configurazioni possibili della rete neurale. Ed è per questo che il valore dei campi magnetici e il comportamento delle interazioni di scarica tra due neuroni non può essere determinato direttamente come non può essere determinata la frequenza di apparizione di una configurazione neurale piuttosto che un'altra. (L'interazione di scarica tra neuroni, è bene specificarlo, hanno natura statistica e non fisica poiché i neuroni scaricano simultaneamente, alternativamente o sono entrambi silenti per una ragione funzionale al compito eseguito nelle varie configurazioni della rete e non per un legame esclusivo di natura fisica).
Per questo è più ragionevole partire dai dati a disposizione e cercare all'inverso di determinare il valore dei campi magnetici e delle interazioni neurali di scarica, secondo il modello di Ising. Un tentativo riuscito di questo genere è stato fatto dai ricercatori di Princeton coordinati dal fisico e biologo William Bialek. Sono stati registrati pattern di scarica di 40 neuroni appartenenti alla retina di salamandra in modo da avere una configurazione binaria di scarica neurale. In questo modo ogni neurone è stato catalogato come attivo o silente. Le statistiche riguardanti le configurazione di scarica del sistema retinale sono state poi modellizzate secondo il modello di Ising. Invece di permettere di determinare le dinamiche di scarica neurale delle cellule retinali della salamandra sono stati ottenuti i valori statistici degli accoppiamenti di scarica tra neuroni e ottenuta una panoramica esaustiva del funzionamento della rete neurale retinale.
Questo risultato dell'applicazione del problema inverso di Ising è stato validato in altri contesti sperimentali e in particolare per cellule corticali ottenute in coltura.
Ricostruzione di una rete di geni regolatori
Le proteine sono macromolecole costituite da lunghe catene di aminoacidi. La particolare sequenza di aminoacidi di una proteina è codificata dal DNA. I geni presenti nel DNA producono a loro volta la copia di una parte di DNA a singolo filamento chiamato RNA messaggero che viene tradotto, anche più volte, per costruire le proteine. L'espressione dei geni è il risultato di questo processo di trascrizione e traduzione che viene controllato affinché le proteine siano correttamente prodotte in quantità giuste e nei tempi giusti. Alcune proteine, chiamate fattori di trascrizione, legano il sito di trascrizione di uno o più geni in modo da controllare quantità e tempistiche di trascrizione dei geni in proteine. Tale controllo avviene anche su geni che a loro volta producono fattori di trascrizione in modo da produrre una cascata di eventi che favoriscono la corretta espressione dei geni. I diversi fattori di trascrizione, in aggiunta, combinano i loro effetti per creare una rete di espressione genetica tra più geni.
Uno dei metodi messi a punto per misurare il livello di espressione dei geni è basato sulla trascrizione inversa dell' RNA messaggero e del sequenziamento delle catene nucleotidiche dei frammenti di DNA prodotti. Se so quante catene nucleotidiche sono state prodotte so anche quali sono i livelli di RNA messaggero. In un'unica sessione è possibile tracciare il profilo dell'espressione genetica di oltre 10.000 cellule, marcate individualmente per dare un'identità ad ognuna, e analizzare la risposta dei geni all'introduzione dei fattori di trascrizione nei termini dei livelli di RNA messaggero prodotto. Il sequenziamento di singole cellule, però, distrugge le cellule stesse che non hanno tempo di esprime tutto il loro patrimonio genetico. (Questo tipo di analisi avviene solo per saggiare i livelli di RNA messaggero e non delle proteine). Per questo, come nel caso delle interazioni tra neuroni, l'obbiettivo nella formulazione del problema inverso di Ising è quello di trovare un modello statistico che descriva i dati a disposizione ottenuti dal sequenziamento del DNA e poi trovare le relazione di rete tra i geni per ogni data immissione di fattori di trascrizione. In particolare dai livelli di RNA messaggero prodotto a seconda di uno o l'altro dei fattori di trascrizione introdotti, e quindi dall'esistenza di un certo numero di stati differenti del sistema di espressione genetica, si potrà ottenere una stima di quali sono i geni che hanno una espressione tra loro correlata. L'espressione dei geni può essere trattata attraverso una variabile binaria che assuma i valori 1/-1 per, "gene attivo"/"gene spento" a seconda che il loro grado di espressione misurato in livelli di RNA messaggero superino una certa soglia prefissata. L'interazione a coppie è quella determinabile attraverso la funzione modello prima esaminata nella prima formula, funzioni che, attraverso adeguate trasformazioni matematiche, possono essere applicate anche ad interazioni tra più di due geni.
Un'altra metodica interessante per ottenere il livelli di RNA messaggero e inferire le interazioni a rete tra i geni dai livelli di espressione manifesti è quella di marcare il DNA sminuzzato da una moltitudine di frammenti di RNA messaggero, ottenuti per trascrizione inversa, con sostanze fluorescenti e innestare su un chip i frammenti di DNA marcato. Il livello di fluorescenza sarà legato al livello di RNA presente così come il segnale emesso conseguentemente dal chip.
Determinazione della struttura delle proteine
La struttura tridimensionale delle proteine, lunghe catene di aminoacidi, determina le proprietà fisico/chimiche della proteina e il modo in cui interagisce con le altre strutture biologiche. Ci sono due metodi maggiormente usati per determinare la struttura tridimensionale di una proteina a partire dalla sequenza di aminoacidi. L'approccio computazionale cerca la struttura tridimensionale con il più basso livello di energia a partire dalle forze che legano tra di loro i singoli aminoacidi. Il secondo approccio deriva dai dati relativi all'evoluzione delle proteine in diverse specie. Si studiano proteine provenienti da diverse specie con medesima struttura tridimensionale ma con differenze nella catena di aminoacidi. Se sostituiamo a due aminoacidi legati e vicini nella loro struttura tridimensionale due aminoacidi ugualmente legati la struttura tridimensionale non cambia. Per questo ci si aspetta che esistano dei legami tra aminoacidi vicini nella struttura tridimensionale e che dalle correlazioni tra aminoacidi in catena lineare si possa inferire la forma tridimensionale delle proteine. Purtroppo nascono complicazioni in virtù del fatto che le correlazioni tra aminoacidi in catena lineare sono transitive. Se un aminoacido in posizione i è prossimo e correlato ad uno in posizione j e quello in posizione j è correlato per qualche ragione con un aminoacido lontano nella catena in posizione k, i sarà correlato con k. Per questo dalle correlazioni tra aminoacidi in catena lineare non si può facilmente inferire la forma tridimensionale. In questo caso è ancora utile l'approccio inverso, dalle correlazioni che si possono trovare in diverse specie nella forma tridimensionale delle proteine si possono inferire frequenze e correlazioni tra gli aminoacidi in sequenza lineare. Il problema statistico inverso si basa sulla soluzione dell'Hamiltoniana:
Ciò che è noto sono gli aminoacidi e le posizioni di aminoacidi rappresentati in una sequenza i = 1,2,3....N . Ciò che è da trovare sono l'energia di legame tra due aminoacidi il cui valore è rappresentato nell'Hamiltoniana nello stesso modo J in cui nel problema inverso di Ising erano rappresentati i valori di interazione magnetica tra due spin, ogni correlazione J contribuisce in una certa misura all'energia totale H. Da trovare sono anche le frequenze di presenza di un dato aminoacido che è rappresentato come venivano rappresentati i valori dei campi magnetici nel problema inverso di Ising (h). Le frequenze di aminoacidi e l'energia che lega coppie di aminoacidi cercate nella nostra sequenza saranno tali da riprodurre correlazioni e frequenze di aminoacidi differenti osservate nelle diverse specie.
Conclusioni
Il problema inverso di Ising sorge nel contesto di diversi problemi connessi con l'inferenza dei parametri di un modello. Esso sorge in maniera più chiara quando gli enti osservati possono essere paragonati a spin di Ising, che assumono valori binari, con correlazioni a coppie tra questi spin. Secondariamente il problema inverso di Ising sorge anche quando abbiamo una descrizione statistica del comportamento di solo alcune qualità di una situazione osservabile e misurabile, come ad esempio nella determinazione della forma tridimensionale di una proteina o del comportamento di una rete neurale. Ciò nonostante e con adeguate modifiche le funzioni che regolano il modello di Ising (formule 1 e 2 ) possono essere estese anche a tre o quattro valori di spin, anche se, in questo caso, le inferenze non sono ancora state applicate.


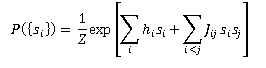
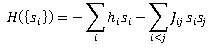



Ho trovato quest’articolo di ottima qualità; ho dovuto però rispolverare, con piacere, un pò di teoria Hamiltoniana, Lagrangiana e di meccanica statistica, prima di poter accedere all’articolo. Ho notato come l’autore passi con disinvoltura dalla fisica statistica alla biologia del DNA ed RNA alle reti neurali e alla struttura delle proteine. Questo modello importante, ideato da Ising nel 1924 nel caso monodimensionale, poi risolto successivamente per n dimensioni, risulta ancora oggi molto valido per svariati campi di ricerca, come ha potuto ben dimostrare l’autore in questo articolo.
Articolo complesso da leggere in modo scrupoloso e attento, specie per chi non ha dimestichezza o non ha mai avuto dimestichezza con tali argomentazioni. Grazie.