
Sul blog di Elettronica Open Source puoi leggere non solo tutti gli articoli Premium riservati agli abbonati Platinum 2.0 e inseriti nella rivista Firmware 2.0 (insieme ad articoli tecnici, progetti, approfondimenti sulle tecnologie emergenti, news, tutorial a puntate, e molto altro) ma anche gli articoli della Rubrica Firmware Reload. In questa Rubrica del blog abbiamo raccolto gli articoli tecnici della vecchia rivista cartacea Firmware, che contengono argomenti e temi evergreen per Professionisti, Makers, Hobbisti e Appassionati di elettronica. I convertitori AD rappresentano una pietra miliare dell’elettronica moderna senza la quale l’elaborazione numerica e la trasmissione digitale dei segnali non sarebbero nemmeno pensabili. In questo articolo ne discuteremo le architetture. Particolare enfasi sarà data ad una serie di considerazioni sui convertitori AD più diffusi nell’elettronica applicata: gli ADC ad approssimazioni successive (SAR).
Un convertitore analogico-digitale o ADC (Analog to Digital Converter), è un circuito elettronico in grado di convertire un segnale analogico con andamento continuo, generalmente una tensione, in una serie di valori discreti esprimibili in forma binaria (in pratica l’operazione opposta a quella eseguita da un DAC, convertitore digitale- analogico). I convertitori AD rappresentano una pietra miliare dell’elettronica moderna senza la quale l’elaborazione numerica e la trasmissione digitale dei segnali non sarebbero nemmeno pensabili. In questo articolo ne discuteremo le architetture. Dal controllo dei processi al campo video, dalle applicazioni nelle telecomunicazioni al campo delle tecniche hi-fi digitali, l’acquisizione, l’elaborazione e la trasmissione dei segnali è ormai oggi quasi interamente digitale. A differenza del segnale analogico, quello digitale è una funzione “tempo discreta quantizzata“. In altre parole, un segnale digitale è definito in un insieme numerabile di istanti di tempo generalmente equispaziati ed è dotato di un codominio composto da un insieme discreto e finito di valori. Una volta codificati in forma binaria questi valori assumono la caratteristica di presentare una reiezione ai disturbi impensabile per un segnale analogico. Questo rende più robusta la trasmissione del segnale stesso. La possibilità di essere elaborato più facilmente dei segnali analogici mediante algoritmi numerici e di essere registrato più facilmente in maniera più fedele e stabile nel tempo sono altri due pregi non trascurabili. Per poter essere trattato in maniera numerica un segnale deve tuttavia prima essere convertito da analogico a digitale. La conversione A/D di un segnale analogico comporta le seguenti operazioni:
- campionamento (discretizzazione del tempo);
- quantizzazione (discretizzazione dell’ampiezza);
- codifica binaria dei quanti.
Il campionamento consente di ottenere una successione di valori istantanei corrispondenti agli istanti di campionamento che si susseguono con una frequenza detta frequenza di campionamento (Figura 1 - dal segnale si estrae un campione ogni intervallo di tempo Tc detto periodo di campionamento). La conversione AD comporta quindi la discretizzazione sia dell’asse dei tempi che di quello delle tensioni.
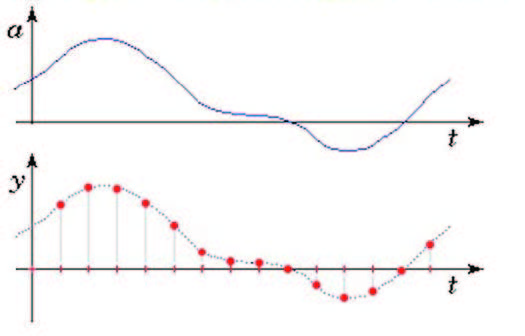
Figura 1: Concetto di campionamento: estrazione dei campioni dal segnale ad intervalli di tempo equispaziati (Tc: periodo di campionamento)
Poiché il risultato di questo processo è una rappresentazione incompleta del segnale originario, è importante che il segnale vari lentamente rispetto alla frequenza di campionamento, poiché solo in queste condizioni rimane circa costante e pari al valore campionato in tutto l’intervallo di campionamento. Questo aspetto abbastanza intuitivo può essere meglio formalizzato in termini di aliasing, fenomeno la cui analisi porta a concludere che è necessario campionare sempre ad una frequenza superiore al doppio della massima frequenza contenuta nel segnale analogico originario (Teorema di Nyquist-Shannon). A questo aspetto è legato anche l’impiego spesso di un filtro passa-basso a monte del campionatore che delimiti con certezza la banda del segnale. Il segnale analogico in ingresso all’ADC tipicamente presenta dinamica non superiore a 10-20Vpp e la codifica finale può essere di tipo binaria naturale oppure BCD (particolarmente utile nel caso in cui si debba rappresentare il risultato su un visualizzatore decimale) o di altra natura. I dati in uscita possono essere forniti in formato parallelo cioè su n linee, tante quante sono i bit del convertitore oppure in formato seriale cioè su di un’unica linea. I tempi di conversione possono variare da alcuni millisecondi a pochi nanosecondi e la velocità di campionamento può arrivare a centinaia di MSPS (milioni di campioni al secondo) a seconda dell’architettura dell’ADC. Il funzionamento di un’ADC ideale è in ogni caso completamente definito una volta assegnati:
- numero di bit di codifica;
- frequenza di campionamento;
- minima variazione dell’ingresso (passo di quantizzazione o LSB) in grado di produrre una variazione dell’uscita.
L’associazione tra livello quantizzato e relativo codice prende il nome di codifica. I codici rappresentativi dei campioni sono in ogni caso una loro approssimazione numerica. Per i segnali bipolari il codice è del tipo binario con offset nel senso che si fa corrispondere tutti zero al fondo scala negativo (-FS) e tutti 1 al fondo scala positivo (+FS).
QUANTIZZAZIONE ED ERRORE DI QUANTIZZAZIONE
La dinamica di ingresso [Vmin,Vmax] di un ADC è suddivisa in un numero di intervalli pari ad una potenza di 2 e ad ogni intervallo è associato un codice. La transcaratteristica dell’ADC, da intendere come caratteristica statica, esprime appunto questo concetto. Quest’ultima può essere non silenziata oppure silenziata (Figura 2).
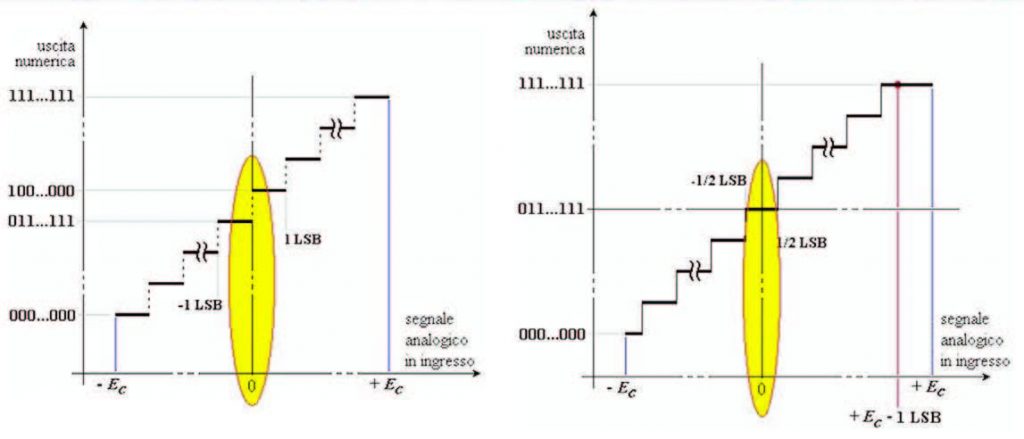
Figura 2: Caratteristica di quantizzazione bipolare ideale non silenziata (a sinistra) e silenziata (a destra)
Nel primo caso, un campione di valore nullo produce sempre un valore numerico non nullo. Il rumore sovrapposto al segnale è ciò che determina quindi la codifica effettiva di un campione di valore nullo. In una quantizzazione silenziata invece, un intervallo di quantizzazione è sempre “centrato” sullo zero per cui tutti i campioni compresi tra - ½ LSB e + ½ LSB vengono associati al codice zero, pertanto è sempre garantita una certa reiezione al rumore sovrapposto al segnale nell’intorno dello zero. La Figura 3 esemplifica, per una codifica a tre bit, quanto espresso nella forma più generale possibile dalla precedente Figura 2.
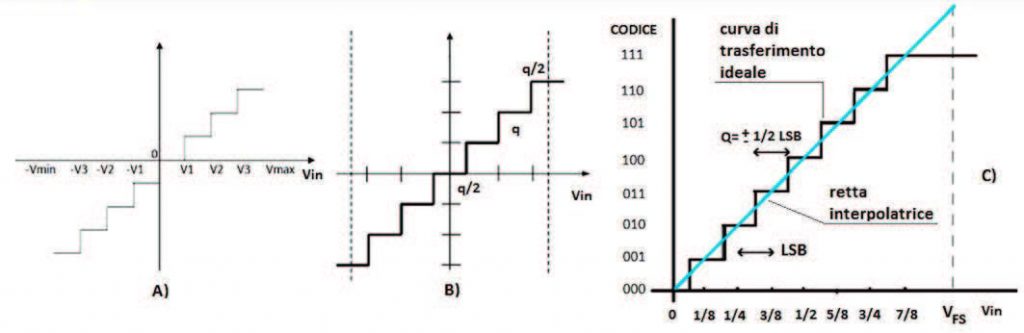
Figura 3: Caratteristiche di quantizzazione (ideali) per convertitore AD a tre bit (rispettivamente non silenziata bipolare, silenziata bipolare e silenziata unipolare)
La caratteristica non è in ogni caso biunivoca poiché, nota la tensione in ingresso, è univocamente determinata l’uscita, tuttavia, nota l’uscita non è definibile univocamente l’ingresso. L’errore massimo dovuto alla sola quantizzazione è comunque pari a ±q/2 dove q è il passo di quantizzazione pari ad 1 LSB. Evidentemente, l’errore di quantizzazione pesa tanto più quanto più piccolo è il valore del campione e può essere ridotto agendo sull’ampiezza della dinamica in ingresso e/o sul numero di intervalli in cui questo è suddiviso e quindi indirettamente sul numero di bit utilizzati per la codifica. In alcuni casi è possibile utilizzare quantizzazioni non uniformi al fine di ridurre l’errore assoluto massimo di quantizzazione per i campioni di minore valore a scapito dell’errore assoluto massimo per campioni di maggior valore ottenendo un errore massimo relativo circa costante. Le quantizzazioni non uniformi possono inoltre scaturire da considerazioni sulla statistica del segnale. Si può cioè imporre una caratteristica di quantizzazione che preveda un maggior numero di quanti di ampiezza più piccola in corrispondenza delle fasce di valori più probabili a scapito di altre fasce di valori cui assegnare quanti più ampi e che pur essendo di conseguenza gravati da maggiore incertezza di quantizzazione risultano comunque improbabili per quanto possibili. La quantizzazione non uniforme è in ultima analisi utile quando la statistica del segnale non è uniforme. Per esempio, nei sistemi digitali di conversione del segnale vocale la quantizzazione è tipicamente logaritmica. Qualunque valore Vin del segnale di ingresso che cade in un certo intervallo, viene associato sempre allo stesso codice. La quantizzazione comporta pertanto implicitamente un errore di quantizzazione (Figura 4).
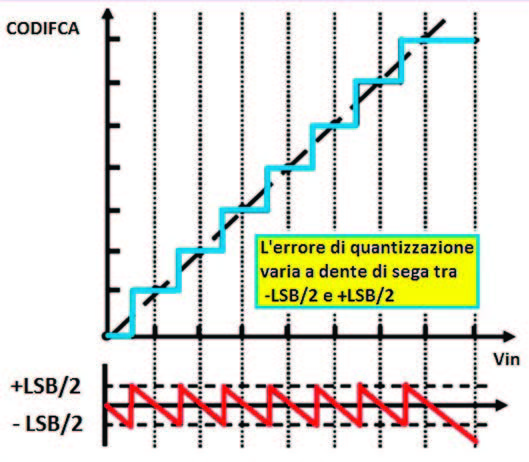
Figura 4: Legame tra caratteristica di trasferimento ed errore di quantizzazione
Quanto più sono piccoli e quindi numerosi i quanti, cioè quanto maggiore è il numero di bit fissata la dinamica, tanto inferiore è tale errore. L’errore massimo di quantizzazione discende direttamente dalla caratteristica di trasferimento ed è pari a ±½ LSB. L’errore complessivo dipende tuttavia anche dalla presenza di eventuali disturbi e dalla non idealità circuitale del convertitore. Influenza il tutto anche il valore del campione: al centro di un livello di quantizzazione, anche se al segnale si sovrappone un disturbo, il codice di uscita non cambia, al confine tra una zona di quantizzazione e l’altra invece basta un piccolo disturbo per modificare il codice di uscita.
SAMPLE-HOLD
Poiché l’ADC non può effettuare la conversione istantaneamente, il valore campionato deve rimanere costante e stabile durante il tempo di conversione. Se così non fosse, il circuito comincerebbe con il processare un quanto di un determinato valore e terminerebbe quando il quanto ha modificato il suo valore. Un circuito d’ingresso detto sample-hold immagazzina allora il campione impiegando un condensatore di tenuta ed un interruttore elettronico per disconnettere il condensatore dall’ingresso e predisporlo per una nuova operazione di campionamento. Ovviamente, il sample-hold introduce esso stesso un piccolo disturbo al segnale e a ciò si aggiunge l’effetto della banda passante non infinita propria di questa parte di front-end del convertitore.




