
Nella puntata precedente “Corso di Elettronica per ragazzi - Puntata 5” abbiamo iniziato la parte pratica del corso di elettronica introducendo il Multimetro digitale, il nostro primo strumento di misura di questo corso, e come impostarlo per misurare il valore della tensione, della corrente e della resistenza dei resistori. Poi, abbiamo visto come fare lo schema elettrico del nostro primo CIRCUITO ELETTRICO che abbiamo anche realizzato in pratica e di cui abbiamo misurato la tensione ai capi di un resistore e la corrente circolante nel circuito, generata dalla batteria. Inoltre, abbiamo utilizzato questa esercitazione di laboratorio per introdurre con calcoli ed esempi la LEGGE DI OHM. In questa puntata tratteremo i PRINCIPI DI KIRCHHOFF e il collegamento in serie di resistori. Infine, metteremo in pratica le nozioni teoriche con un’altra esercitazione di laboratorio.
Introduzione
L’analisi e la progettazione dei circuiti elettrici ed elettronici si basa su due importanti principi dell’elettrotecnica e dell’elettronica: la Legge di Kirchhoff delle correnti e la legge di Kirchhoff delle tensioni.
I nodi e le maglie di un circuito
La comprensione e la formulazione dei principi di Kirchhoff richiede di considerare che un circuito è costituito da nodi e maglie. Quindi, di seguito, diamo la definizione di nodo e di maglia. Un nodo è un punto di un circuito a cui sono collegati almeno due componenti del circuito. Chiariamo con alcuni esempi il concetto di nodo. Se riprendiamo lo schema elettrico del circuito che abbiamo realizzato nella Puntata 5 e lo riportiamo in Figura 1, notiamo che questo circuito ha due nodi che chiamiamo con la lettera “a” e “b”. Al nodo “a” sono collegati il polo positivo della batteria B1 e un terminale del resistore R1, mentre al nodo “b” sono collegati il polo negativo della batteria B1 e l’altro terminale del resistore R1.
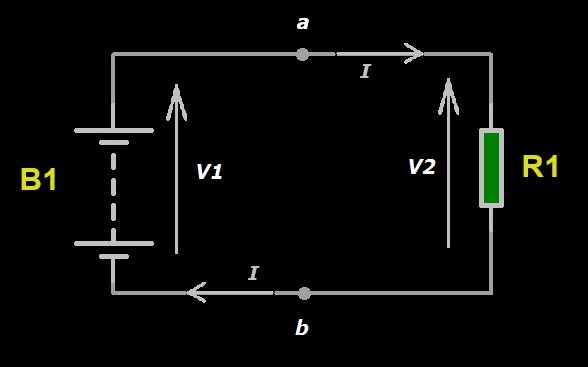
Figura 1: Due nodi di un circuito
Nello schema elettrico mostrato nella Figura 2, con le lettere “a”, “b” e “c” sono indicati tre nodi del circuito.
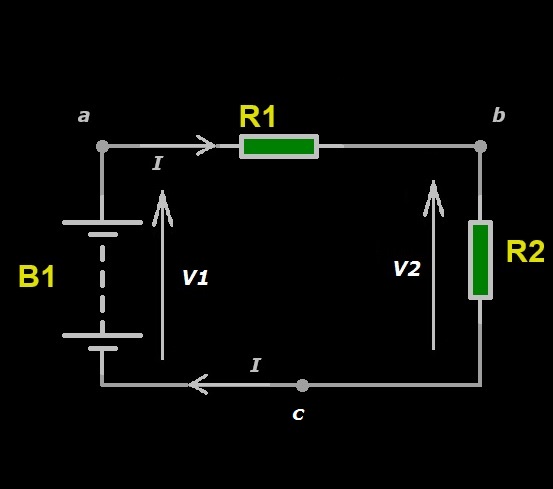
Figura 2: Tre nodi di un circuito
In pratica, è lo stesso circuito della Figura 1 a cui abbiamo inserito il resistore R1 in serie al resistore R2. Al nodo “a” sono collegati il polo positivo della batteria B1 e un terminale del resistore R1; al nodo “b” sono collegati l’altro terminale del resistore R1 e un terminale del resistore R2; al nodo “c” sono collegati il polo negativo della batteria B1 e l’altro terminale del resistore R2. Definito il significato di nodo di un circuito, diamo la definizione di maglia e andiamo a vedere che cos’è una maglia di un circuito. Una maglia è una zona chiusa di un circuito costituita da due o più nodi in sequenza che inizia da un nodo e finisce richiudendosi nello stesso nodo. I circuiti di Figura 1 e Figura 2 sono costituiti da una sola maglia, rispettivamente a-b-a (o b-a-b) e a-b-c-a (o c-a-b-c), a seconda se è percorsa in senso orario o antiorario. Il circuito mostrato in Figura 3, lo stesso di Figura 2 con l’inserimento del resistore R3 in parallelo al resistore R2, è formato da una serie di tre nodi: “a” “b” e “c”, e due maglie, maglia 1: a-b-c-a, e maglia 2: b-c-b, considerando il verso di percorrenza orario.
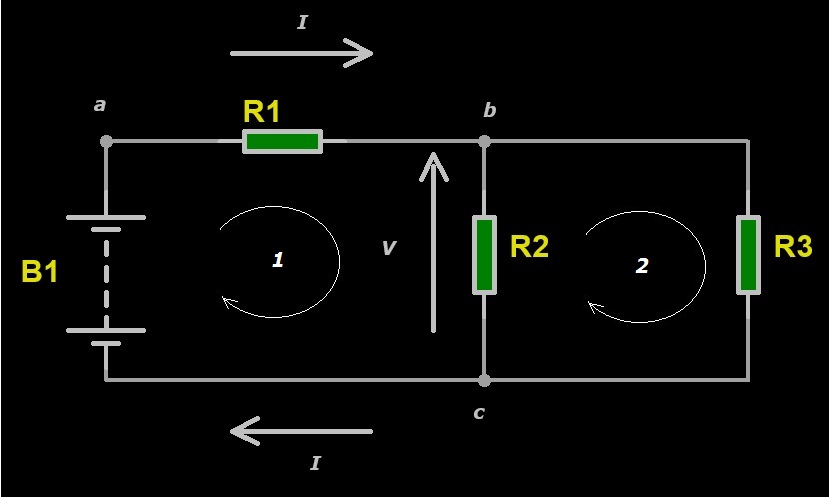
Figura 3: Circuito con tre nodi e due maglie
Le Leggi di Kirchhoff
L’identificazione esatta dei nodi e delle maglie di un circuito ci consente di analizzare il funzionamento di qualsiasi circuito calcolando le correnti che si diramano dai nodi e le tensioni in una maglia.
Legge di Kirchhoff delle correnti
Per quanto riguarda il calcolo delle correnti in un circuito, ci può essere molto utile la Legge di Kirchhoff delle correnti (LKC) così definita: La Legge di Kirchhoff delle correnti afferma che la corrente entrante in un nodo è equivalente alla corrente che esce da quel nodo, ovvero, la somma delle correnti entranti in un nodo è uguale alla somma delle correnti uscenti dal dodo. Chiariamo la LKC con un esempio servendoci ancora dello schema elettrico di Figura 3 modificato con l’indicazione delle correnti fluenti nel circuito che riportiamo in Figura 4.
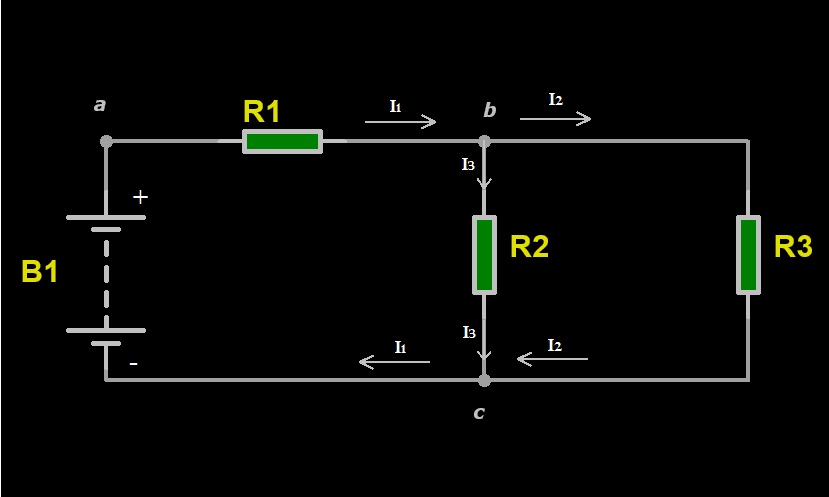
Figura 4: Correnti nel circuito
Seguendo il verso di riferimento delle correnti, che in questo esempio decidiamo che abbiano il verso positivo quando entrano in un nodo e negativo quando escono dal nodo (ma possiamo anche decidere arbitrariamente il contrario) e ricordando che per convenzione la corrente scorre dal potenziale positivo al potenziale negativo, la corrente I1, proveniente dal polo positivo della batteria, supera senza diramazioni il nodo “a” e attraversa il resistore R1 ed entra nel nodo “b”. Dal nodo “b” escono due correnti, I2 e I3. La corrente I2 attraversa il resistore R2, mentre la corrente I3 attraversa il resistore R3 e tutte e due le correnti entrano nel nodo “c”. Per quanto affermato dalla LKC, la corrente I1 entrante nel nodo “b” è uguale alla corrente uscente dallo stesso nodo costituita dalle due correnti I2 e I3. Possiamo quindi scrivere con un’equazione quanto scritto sopra:
I1 = I2+I3
Questa equazione si può tradurre anche così:
I1-I2-I3=0
Come possiamo notare, questa equazione ci conferma che per la LKC, in un nodo la somma algebrica delle correnti è nulla. La corrente I1 generata dalla batteria, dopo aver attraversato tutti gli elementi del circuito (chiuso), ritorna verso il polo negativo della batteria. Ora analizziamo le correnti nel nodo “c”. Nel nodo “c” le correnti entranti sono I2 e I3, mentre I1 è la corrente uscente. Quindi, per la LKC avremo:
-I1+ I2+I3=0
Se isoliamo I1, abbiamo:
I1 = I2+I3
Di nuovo tornano i conti! La corrente I1 è la corrente totale circolante nel circuito. E’ importante tener presente che i versi reali delle correnti si potranno scoprire solo dopo aver calcolato il valore di ogni corrente, come vedremo più avanti nel corso con esempi.
Legge di Kirchhoff delle tensioni
La Legge di Kirchhoff delle tensioni (LKT) si applica alle maglie di un circuito ed è così definita: La Legge di Kirchhoff delle tensioni afferma che in una maglia di un circuito la somma algebrica delle tensioni in tutta la maglia è nulla. Vediamo con un esempio di comprendere meglio la LKT. Nello schema elettrico mostrato in Figura 5 applichiamo la LKT alla maglia a-b-c-a.
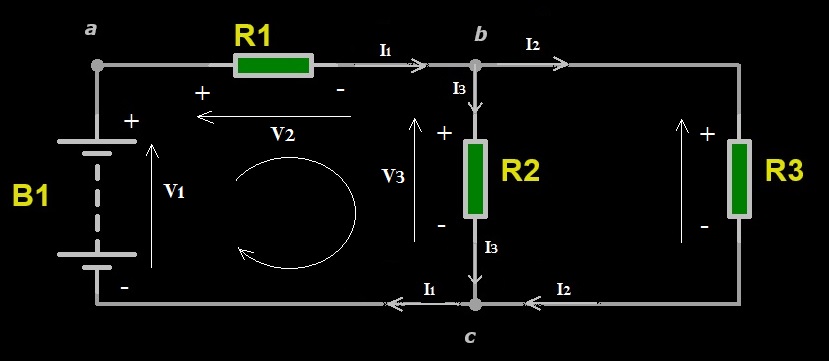
Figura 5: Tensioni nella maglia a-b-c-a
Notiamo il verso delle tensioni V1, V2 e V3 disposte nella maglia a-b-c-a. Il polo di potenziale positivo delle tensioni è il polo di provenienza della corrente che fluisce in ogni elemento, infatti, come abbiamo detto in varie occasioni, la corrente (convenzionale) scorre dal potenziale positivo verso il potenziale negativo. Ora dobbiamo fare la somma delle tensioni scegliendo il verso orario della maglia. Si sommano le tensioni che hanno lo stesso verso sottraendo quelle con verso contrario. Le frecce indicano il verso delle tensioni, ovvero la punta della freccia indica il polo positivo della tensione, come mostrato in Figura 5. Seguendo il verso orario della maglia si ottiene quindi la seguente equazione della LKT:
V1-V2-V3=0
Infatti, le tensioni V2 e V3 che hanno verso concorde hanno verso contrario rispetto a V1. L’equazione precedente possiamo riscriverla rispetto a V1:
V1=V2+V3
Questa equazione dimostra che la tensione della batteria si ripartisce fra i due resistori nella misura che dipende dalle correnti I1 e I3 e dal valore di resistenza dei resistori R1 e R2.
Collegamento di resistori in un circuito
Nelle puntate precedenti abbiamo parlato del resistore come di un elemento conduttore che possiede una resistenza al passaggio della corrente. In questa parte del corso vedremo che in un circuito due o più resistori possono essere collegati IN SERIE e IN PARALLELO.
Resistori in serie
Due o più resistori si dicono in serie quando sono attraversati dalla stessa corrente. La resistenza risultante dal collegamento in serie di resistori è equivalente alla somma della resistenza di ogni resistore della serie. Spieghiamo con un esempio la definizione sopra citata mostrando lo schema elettrico della Figura 6.
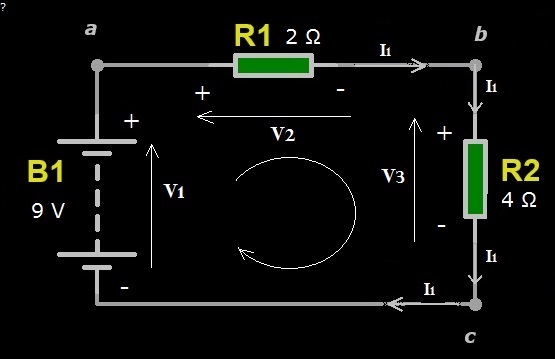
Figura 6: Schema elettrico di un circuito con resistori in serie
Il circuito di Figura 6 ha una sola maglia e tre nodi ed è costituito da una batteria da 9 V e due resistori, R1 di resistenza 2 Ω e R2 di resistenza 4 Ω. Come si può notare dallo schema, nel circuito scorre una sola corrente, la I1, che attraversa i due resistori che quindi per definizione sono in serie. Ora, applichiamo le leggi di Kirchhoff al circuito. Per quanto riguarda la LKC, la corrente ai nodi è la sola I1, mentre per la LKT si ha:
V1-V2-V3=0
che per la legge di Ohm possiamo scrivere anche con:
V1-R1*I1-R2*I1=0
Ma, dalla definizione di resistori in serie, la resistenza totale è la somma della resistenza di R1 e R2. Quindi, al posto dei due resistori si possono sostituire i resistori R1 e R2 con un solo resistore di resistenza R1+R2=6 Ω. Il nuovo schema elettrico risultante sarà un circuito con il resistore equivalente alla somma della serie di R1 e R2, come quello riportato in Figura 7.
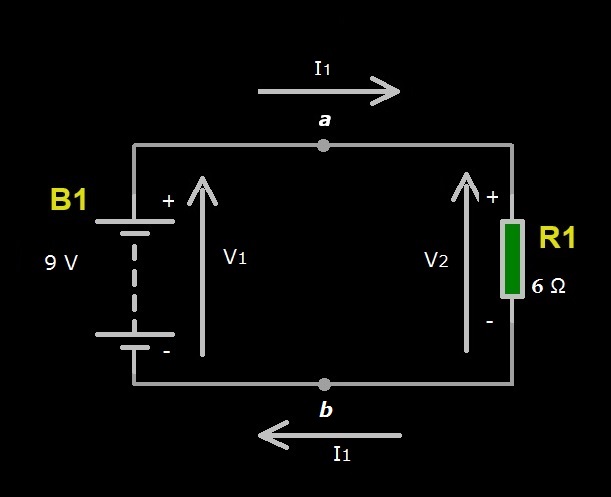
Figura 7: Schema elettrico del circuito con il resistore equivalente alla serie di R1 e R2
Applicando a questo circuito la LKT si ottiene: V1-V2=0 o anche V1-R1*I1=0 da cui, sostituendo i valori di tensione della batteria e di resistenza del resistore R1, abbiamo l’equazione finale seguente: 9 V – 6*I1 =0 da cui 9 V = 6*I1. Quest’ultima equazione evidenzia il fatto che la tensione di batteria si dispone tutta ai capi del resistore R1. Infine, applicando la legge di Ohm si ha I= V / R, e possiamo ricavare la corrente I1 che circola nel circuito:
I1 = V1 / R1 = 9 / 6 = 1,5 A
Pertanto, con una batteria da 9 V collegata ad un resistore di resistenza 6 Ohm, nel circuito scorre una corrente di 1,5 A, ma questo è solo un esempio!
Il partitore di tensione
Riguardo i resistori in serie, abbiamo visto che in un circuito come quello mostrato in Figura 6 in cui sono presenti dei resistori in serie, applicando la LKT, si ottiene l’equazione V1-V2-V3=0 da cui si ha che V1=V2+V3. La relazione V1=V2+V3 ci dimostra che la tensione V1, nel nostro esempio rappresentata da una batteria, si ripartisce ai capi dei due resistori che, appunto, con questo collegamento in serie hanno la funzione di partitore di tensione. In pratica, quando occorre avere una tensione di un determinato valore da ricavare da una sorgente di alimentazione, o da un’altra tensione, possiamo scegliere il giusto valore dei resistori partitori di tensione per ottenere ciò. Vediamo con un esempio quanto affermato utilizzando di nuovo il circuito di Figura 6 che riportiamo per comodità di lettura nella Figura 8.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2499 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.






