
Nella precedente puntata del Corso di Elettronica per ragazzi abbiamo trattato le leggi di Kirchhoff con esempi teorici e pratici. Abbiamo introdotto i circuiti resistivi parlando del partitore di tensione resistivo di cui abbiamo eseguito anche un’esercitazione pratica di laboratorio con misure di corrente e tensioni. In questa puntata, proseguiremo con i circuiti resistivi con la teoria e la pratica dei circuiti con resistori in parallelo che realizzano il partitore di corrente resistivo. Anche per questo argomento utilizzeremo ancora l’analisi nodale e delle maglie con le leggi di Kirchhoff delle correnti (LKC) e delle tensioni (LKT) e la legge di Ohm.
Introduzione
Nella precedente puntata abbiamo trattato circuiti con resistori collegati in serie e abbiamo compreso con la teoria e la pratica con un’esercitazione di laboratorio, che i resistori in serie sono percorsi dalla stessa corrente, ovvero hanno in comune la corrente che li attraversa. Quindi, siano due o più resistori in serie, i resistori hanno in comune la stessa corrente, diversamente dalla tensione che, come enunciato dalla legge di Ohm V=RI, si dispone ai capi di ogni resistore con un valore che dipende dal valore della resistenza elettrica del resistore e dalla corrente. Come vedremo nel prossimo paragrafo, la situazione è diversa nel caso di circuiti con resistori in parallelo (Figura 1 - Circuito con resistori in parallelo) che, come vedremo, realizzano il partitore di corrente.
Resistori in parallelo - Il partitore di corrente
Diversamente dai resistori in serie che hanno in comune la corrente, i resistori in parallelo si definiscono tali perché hanno la tensione in comune, ovvero la tensione ai capi di ogni resistore in parallelo ha lo stesso valore. Per quanto riguarda la corrente, come vedremo con calcoli ed esempi, dalla legge di Ohm I=V/R, in ogni resistore collegato in parallelo il valore della corrente dipende dal valore della resistenza e dalla tensione applicata. La Figura 1 mostra un circuito con resistori collegati in parallelo.
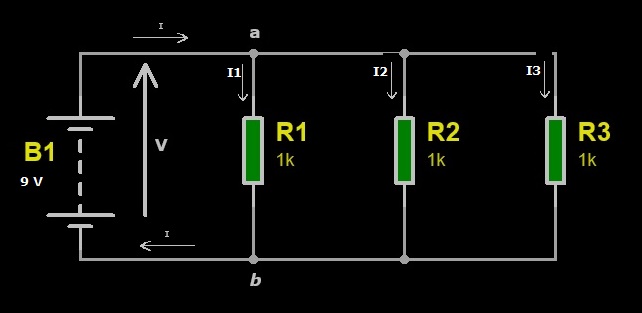
Figura 1: Circuito con resistori in parallelo
Osserviamo che il circuito di Figura 1 ha due nodi, pertanto per l’analisi nodale delle correnti che scorrono nel circuito ricorriamo alla Legge di Kirchhoff delle correnti (LKC) di cui riportiamo la definizione:
La Legge di Kirchhoff delle correnti afferma che la corrente entrante in un nodo è equivalente alla corrente che esce da quel nodo, ovvero, la somma delle correnti entranti in un nodo è uguale alla somma delle correnti uscenti dal nodo.
Quindi, applicando la LKC e considerando positive le correnti entranti nel nodo e negative quelle uscenti (ricordiamo che possiamo scegliere anche il contrario), possiamo scrivere l’equazione delle correnti seguente:
I-I1-I2-I3=0
Se cambiando segno portiamo I1, I2 e I3 a destra del simbolo = possiamo anche scriverla così:
I=I1+I2+I3
Questa relazione è molto utile per capire cosa succede alle correnti nel circuito: la batteria B1 genera la corrente I (ricordiamo che in realtà la batteria (un generatore) non genera corrente ma, grazie alla sua differenza di potenziale mette in movimento gli elettroni liberi nei conduttori di collegamento e nei resistori). La corrente I entra nel nodo “a” e si ripartisce in tre correnti nei rispettivi resistori realizzando così un partitore di corrente. Le tre correnti nel loro percorso entrano nel nodo “b” da cui esce la corrente I. Quindi, applicando ancora la LKC al nodo “b” avremo la relazione seguente:
I1+I2+I3-I=0
Anche qui, cambiandogli segno, portiamo I a destra del simbolo = e quindi possiamo anche scrivere l’equazione così:
I1+I2+I3=I
Questa relazione ci conferma che la corrente I generata dalla batteria, uscendo dal polo positivo della batteria, dopo il percorso nel circuito ritorna alla batteria sul polo negativo, infatti, per convenzione, la corrente scorre dal polo (o potenziale) positivo al polo negativo. Anche in questo caso, ricordiamo che in realtà la corrente (il flusso di elettroni) scorre dal potenziale negativo al potenziale positivo. Osservando ancora lo schema elettrico del circuito di Figura 1, notiamo che i tre resistori R1, R2 e R3 hanno lo stesso valore di resistenza di 1 kohm (k sta per 1000, quindi 1000 ohm) e, essendo collegati in parallelo, per definizione ai loro capi c’è la stesso valore di tensione che in questo caso è proprio il valore di tensione della batteria collegata in parallelo ai resistori. Detto questo, utilizzando la legge di Ohm proviamo a calcolare la corrente che scorre in ogni resistore e, dato che hanno lo stesso valore di resistenza e di tensione ai loro terminali, intuiamo sarà di uguale valore in ogni resistore.
Dalla legge di Ohm:
I=V/R
quindi
I1=V/R1 I1=9 V/1000 ohm=0,009 A = 9 mA (essendo il mA la millesima parte dell’ampere, ossia 1 mA = 0,001 A).
Pertanto, I1=I2=I3=9 mA e la corrente totale circolante nel circuito sarà:
I=I1+I2+I3=27 mA
Questo esempio può far nascere una domanda: se le tre correnti I1, I2 e I3 equivalgono ad un’unica corrente I, se si volesse far scorrere la stessa corrente I inserendo nel circuito un solo resistore con resistenza equivalente al valore di resistenza dei tre resistori in parallelo, che resistenza dovrebbe avere quel resistore? Lo scopriremo nel paragrafo seguente in cui vedremo come si calcola la Resistenza equivalente alla resistenza di resistori in parallelo.
Resistenza equivalente di resistori in parallelo
Nella puntata “Corso di Elettronica per ragazzi - Puntata 4” abbiamo parlato della CONDUTTANZA ELETTRICA che esprime la proprietà di un conduttore di condurre una corrente elettrica. Concettualmente, la conduttanza è l’inverso della resistenza, come espresso dalla relazione G = (1/R)S, dove con la lettera G viene indicata la conduttanza e con la lettera S la sua unità di misura in siemens. Premesso questo, riprendiamo e riportiamo in Figura 2 lo schema elettrico del circuito con resistori in serie e in parallelo che abbiamo realizzato nella precedente puntata e assegniamo un valore a tutti i componenti.
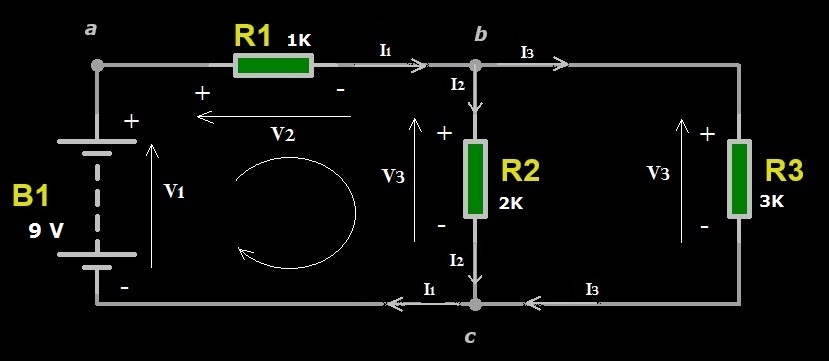
Figura 2: Circuito con resistori in serie e in parallelo
Questo circuito ha tre nodi e due maglie ed è costituito dal resistore R1 in serie al parallelo dei resistori R2 e R3. Per la LKC al nodo “b”, possiamo scrivere la relazione delle correnti seguente:
I1-I2-I3=0
Per la legge di Ohm si ha:
I1=V2/R1 I2=V3/R2 I3=V3/R3
Notiamo che i resistori in parallelo R2 e R3 hanno la stessa tensione V3.
I1=I2+I3 che si può scrivere I1=V3/R2+V3/R3
Quindi, essendo V3 la tensione in comune a R2 e R3:
I1=V3*(1/R2+1/R3) ma, essendo G=1/R, si ha:
I1=V3*(G2+G3)
La conduttanza Gp risultante dal parallelo di R2 e R3 è data dalla seguente relazione:
Gp=I1/V3=G2+G3= 1/R2+1/R3
Svolgiamo la somma delle conduttanze rispetto a R:
Gp=1/R2+1/R3=R2+R3/R2*R3
Quindi, il valore della resistenza risultante dal parallelo di due resistori si ottiene dividendo la somma delle due resistenze per il loro prodotto.
Calcoliamo il valore della resistenza equivalente Rp del parallelo dei due resistori R2 e R3:
Essendo Gp=1/Rp si ottiene:
Rp=1/Gp= (R2*R3)/(R2+R3)
Sostituiamo i simboli con il loro valore:
Rp=(2K*3K)/(2K+3K)= 6K2/5K=1,2K=1200 ohm
A questo punto, dato che abbiamo calcolato il valore della resistenza equivalente alla resistenza dei due resistori in parallelo, possiamo sostituire il parallelo R2-R3 con il resistore Rp di resistenza Rp, come mostrato nel circuito di Figura 3 equivalente al circuito di Figura 2.
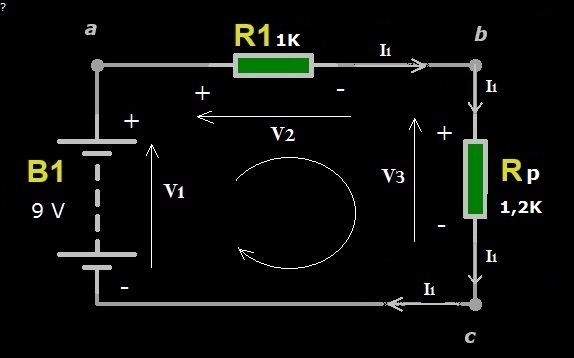
Figura 3: Circuito con resistore equivalente al parallelo di R2 e R3
Come si può notare, il circuito di Figura 3 risulta essere semplificato rispetto al circuito di Figura 2 in quanto è un semplice partitore di tensione costituito da due soli resistori in serie e una sola maglia. In questo modo, è molto semplice ricavare rapidamente il valore della corrente I1 e le tensioni V2 e V3 mediante la legge di Ohm. Possiamo semplificare ulteriormente lo schema elettrico del circuito sostituendo R1 e R2 con un resistore RS la cui resistenza è la somma delle resistenze dei due resistori, ovvero RS=R1+Rp=2,2K, come mostrato nel circuito in Figura 4.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2232 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.







