
Uno dei concetti più misteriosi e intriganti per la giovane matricola di ingegneria è quello di ALU. Sai che è qualcosa che sta dentro la CPU, non sai bene che cos’è né che cosa faccia, ma già perché sta dentro la CPU deve essere qualcosa di incredibile. Hai saputo? Quello si è progettato una ALU! Caspita! Ma in realtà una ALU non è niente di fantascientifico. La ALU è la manodopera della CPU, è il blocco di circuiti che fa tutto il lavoro, ma niente di più. Progettare una ALU significa mettere insieme un po’ di circuiteria in grado di eseguire le operazioni che si vuole che la CPU esegua per noi, ma il suo progetto si riduce sostanzialmente a progettare hardware aritmetico-logico dotato di una certa efficienza. In questo articolo vi parleremo di una serie di circuiti che la vostra CPU potrà usare per svolgere le operazioni più comuni, quelle che sicuramente vorrete che faccia. Il resto è alla vostra fantasia.
POTENZA DI CALCOLO
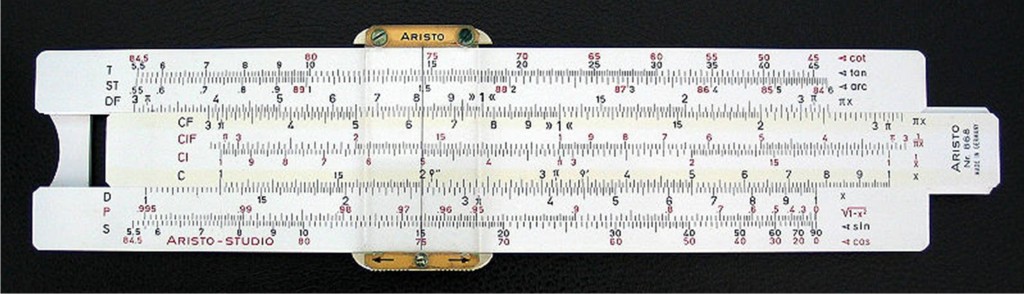
Si sente dire spesso che l’ingegno umano è capace di miracoli, e in effetti è vero. Pensate al computer o al telefono attraverso il quale state leggendo, alla rete di cavi e calcolatori e router e modem e switch che si scambiano incessantemente dati. Pensate ai satelliti attraverso i quali i dati rimbalzano, o alle sonde che si inoltrano nello spazio profondo e questi dati li mandano indietro. Quasi ogni angolo del mondo ormai contiene uno di questi prodigi. Ma si sente dire altrettanto spesso che l’ingegno umano è capace anche di cose tremende, e anche questo è vero. Quello di cui non si sente parlare spesso è di come generazioni di studenti siano state afflitte da una di queste nefandezze. Se frugaste in quello scatolone polveroso che vi guarda da sopra l’armadio, probabilmente trovereste una delle più terrificanti macchine di tortura mai concepite dalla mente umana: il regolo calcolatore (Figura 1).
Gli ingegneri più vecchia scuola che hanno avuto a che fare con questo aggeggio sanno quanto fosse difficile da usare, e allo stesso tempo quanto fosse potente. La prossima volta che passano Apollo 13 in televisione fate caso al passaggio in cui gli ingegneri della NASA utilizzano i regoli per calcolare la traiettoria di rientro della navicella spaziale. Niente calcolatrici, all’epoca: la trigonometria sferica si calcolava su un righello. Gli ingegneri più giovani tra noi, che non hanno avuto di questi problemi, forse sottovalutano l’importanza di avere una buona calcolatrice sotto mano quando si deve fare un progetto, ma ancora oggi, circondati da oggetti in grado di fare calcoli, quella macchinetta piena di tasti è un grande strumento di lavoro.
In effetti, se ci pensate, una calcolatrice è il più semplice computer che possiate concepire: ogni volta che premete un tasto date, alla batteria di circuiti all’interno, una nuova istruzione da eseguire. Certe calcolatrici, addirittura, prima vi fanno inserire gli operandi, e poi decidere la funzione. È come se, da un certo punto di vista, eseguiste a mano due LD dalla vostra testa ai registi della calcolatrice e poi il calcolo desiderato. Una calcolatrice, sostanzialmente, è l’esempio perfetto di ALU: un insieme di circuiti aritmetico-logici che esegue le vostre istruzioni.
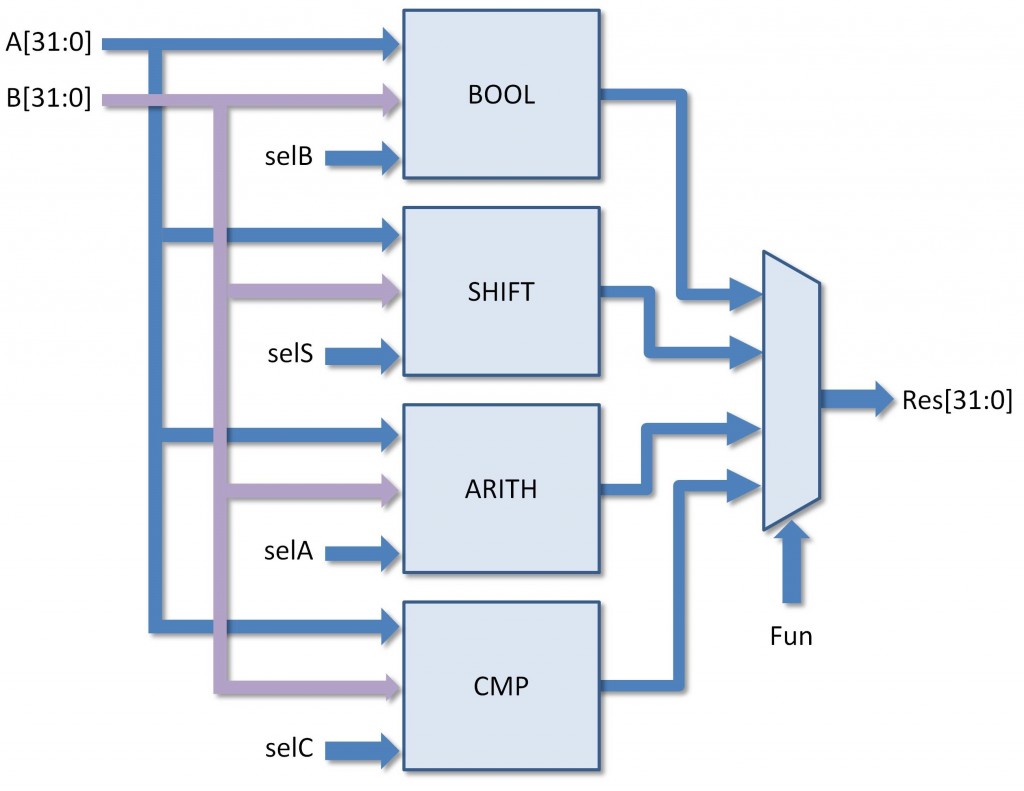
Due sono dunque le cose che ci servono per progettare la ALU: una schiera di circuiti che lavorino in parallelo sui nostri dati, e un modo per selezionare l’uscita (ossia la funzione), che vogliamo (Figura 2). Nel caso della calcolatrice l’ingresso del multiplexer lo decide il tasto che abbiamo premuto; nel caso di un processore dovremo generarlo a partire dall’opcode dell’istruzione corrente. I vari circuiti dovranno avere, oltre agli ingressi dati, anche ulteriori ingressi di selezione: il blocco per le operazioni booleane, ad esempio, vorrà degli ingressi per decidere quale operazione logica eseguire, il blocco per le operazioni aritmetiche vorrà sapere se vogliamo fargli eseguire una somma, una sottrazione, ecc., e così via. Altri blocchi possono essere aggiunti in fondo alla colonna: basta allargare il multiplexer a destra, e ovviamente generare opportunamente i segnali di controllo a partire dagli opcode. Della selezione dei segnali di controllo vi parleremo nel prossimo articolo: qui il problema è cosa mettere dentro gli scatolini. [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 4094 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.







Molto bello l’articolo gia’ solo per il titolo. Complimenti. Uno dei motivi che mi spinsero a studiare informatica nel lontano ’86, fu proprio un articolo apparso sull’appendice scientifica che ogni Mercoledi’ usciva su La Stampa. Era un articolo sul sistema BCD e l’artimetica delle ALU a 4 bit. Bellissimo, ho ancora i brividi.
La figura 15 non mi convince: la porta di uscita non dovrebbe essere una AND?
Infatti da una NOR a 4 ingressi mi aspetto che se sono tutti a 0 l’uscita valga 1, mentre nel circuito di fig.15 se tutti gli ingressi valgono 0, le uscite delle prime due porte valgono 1 e di conseguenza l’uscita della terza porta vale 0; se invece la terza porta fosse una AND il risultato sarebbe corretto.
Sì, hai ragione. La soluzione che suggerisci tu è il teorema di DeMorgan, e va benissimo. Io qui avevo in mente una più semplice fatta da un albero di OR e una NOR in fondo. Si vede che dopo il copia e incolla ho dimenticato di cancellare i pallini! Correggo subito.
Probabilmente l’hai sbagliato di proposito per verificare quanti leggevano attentamente l’articolo. 😉
Esattamente! Con il tuo commento sono balzato a quota due! ?
Grazie per la segnalazione. Modificato.