Demodulare un segnale QPSK con Python

Componenti radio come modulatori, demodulatori e sintonizzatori, sono tradizionalmente implementati con componenti hardware analogici. La radio definita da software consente invece di implementare nel software la maggior parte di questi componenti tradizionalmente basati su hardware. Per poter implementare via software gli algoritmi di modulazione e demodulazione, occorrono degli ambienti di sviluppo che consentano di acquisire i dati, testare e sviluppare le funzioni di trasmissione dei dati e di elaborazione del segnale digitale. Tra gli ambienti disponibili vi è anche il linguaggio di programmazione Python. In questo articolo, vedremo come implementare una modulazione QPSK per SDR mediante il linguaggio Python.

Introduzione

In genere, una radio definita via software (SDR) può essere configurata per selezionare frequenza centrale, frequenza di campionamento, larghezza di banda e altri parametri per trasmettere e ricevere segnali di interesse. Le tecniche di modulazione e demodulazione, invece, vengono sviluppate utilizzando un processo in due fasi:

Sviluppare e ottimizzare gli algoritmi di modulazione e demodulazione per una data frequenza di campionamento, larghezza di banda e ambiente specifico. Questo avviene su un PC host, dove il debug e la visualizzazione sono più semplici.
Prendere l'algoritmo di cui sopra, che può essere implementato in un linguaggio ad alto livello in virgola mobile e adattarlo per essere usato con una piattaforma SDR.

Il primo passaggio richiede un comodo meccanismo per acquisire i dati per l'analisi del segnale e lo sviluppo degli algoritmi di elaborazione. Ciò rende di vitale importanza disporre di un software basato su PC, efficiente e affidabile, in grado di sviluppare e testare le funzioni di trasmissione dei dati e di elaborazione del segnale digitale in un sistema di comunicazioni.

Un ambiente software che soddisfa questo requisito è sicuramente MATLAB. Un'altra architettura software SDR è la popolare GNU Radio, che è open source, e che fornisce blocchi di elaborazione del segnale per implementare radio definite dal software. Può essere utilizzato con hardware RF esterno per creare radio definite via software o senza hardware in un ambiente simile alla simulazione. Infine, anche il linguaggio di programmazione Python può essere utilizzato per lo scopo seppure con tutti i limiti rispetto alle alternative.

Questo articolo si concentra esclusivamente sul primo passaggio algoritmico del processo di sviluppo SDR utilizzando il linguaggio di programmazione Python come ambiente di sviluppo software.

La modulazione PSK

Il miglior modo per introdurre ad un nuovo argomento è sempre quello di fare un esempio pratico. Ecco quindi che andremo ad implementare in Python alcuni degli elementi che costituiscono la catena di elaborazione del segnale in un sistema di comunicazione con modulazione QPSK.

Nella modulazione PSK viene fatta variare la fase ( φ(t) ) del segnale portante, in accordo con il valore del bit o del gruppo di bits che si vuole trasmettere. Il segnale modulato sarà quindi dato da:

s(t) = A cos(ω₀t + φ(t))

A seconda del numero di simboli della modulazione, la fase varierà in un insieme finito di valori. La Tabella 1 riporta questi valori per le modulazioni 2-PSK, 4-PSK e QPSK.

Tabella 1: Relazione tra simboli binari e valori di fase per alcune modulazioni PSK
Modulazione	Simboli	Fasi
2-PSK	[0 1]	[0° 180° ]
4-PSK	[00 01 10 11]	[0° 90° 180° 270°]
QPSK	[00 01 10 11]	[45° 135° 225° 315°]

Nelle simulazioni è sempre conveniente operare in banda base e quindi con segnali complessi. Questo vuol dire che il segnale trasmesso può essere visto come:

s(t) = I(t) cos(ω₀t) + j Q(t) sin(ω₀t) = I(t) + j Q(t)

Dove I(t) = A cos(φ(t)) e Q(t) = A sin(φ(t)) sono, rispettivamente, la componente in fase e in quadratura del segnale modulato.

Se la variabile A è pari ad 1, possiamo rappresentare i simboli delle modulazioni PSK come punti appartenenti alla circonferenza di raggio unitario nel piano di Gauss (o complesso). Sull'asse reale del piano troveranno posto i valori della componente in fase I(t) e sull'asse immaginario quelli della componente in quadratura Q(t), come riportato in Figura 1.

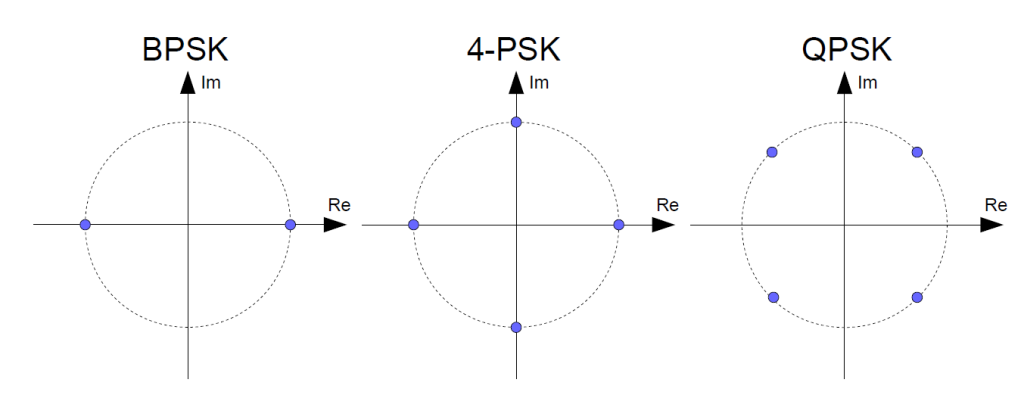
Figura 1: Costellazioni dei simboli complessi per alcune modulazioni PSK

Nella modulazione BPSK i valori oscillano sull'asse reale tra -1 e 1. La componente in quadratura è quindi sempre nulla. Le modulazioni 4-PSK e QPSK possono essere viste come due modulazioni BPSK ortogonali tra loro.

Implementazione Python

Per prima cosa, importiamo le librerie necessarie.

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from commpy.filters import rrcosfilter

Numpy è ormai considerata come la libreria Python standard, quando si tratta di operare con matrici e array. Allo stesso modo, quando si tratta di visualizzare i dati viene utilizzata Matplotlib. Commpy è un pacchetto che implementa algoritmi di comunicazione digitale e risulta molto utile poiché fornisce un'implementazione del filtro RRC.

Nel blocco successivo, vengono impostati i parametri della simulazione.

N = 500 # numero di simboli da trasmettere
SPS = 8 # numero di campioni per simbolo
sync = 1 # se diverso da 0 utilizza blocco recupero tempo di simbolo

SNRdB = 50 # rapporto S/N desiderato
delay = 0/8 # ritardo in frazione di tempo di simbolo: -4/8 <= delay <= 4/8
fo = 0e-6 # offset in frequenza

Andiamo a descrivere questi parametri:

N rappresenta il numero di simboli della sequenza da trasmettere. Ogni simbolo è associato ad un numero complesso, e ogni numero complesso è associato ad uno (BPSK) o più (M-PSK) bit .
SPS indica il numero di campioni per ogni simbolo. Nella pratica, vengono generati più campioni da trasmettere per ogni simbolo, e il motivo ha a che fare con il filtraggio. Particolari filtri (RRC) vengono infatti usati per creare la "forma" dei simboli perché la forma nel dominio del tempo cambia la forma nel dominio della frequenza. Il dominio della frequenza ci informa quanto spettro/larghezza di banda utilizzerà il nostro segnale, e di solito vogliamo ridurlo al minimo. Quando usiamo 1 campione per simbolo, è come trasmettere impulsi rettangolari. Gli impulsi rettangolari non sono efficienti perché utilizzano una quantità eccessiva di spettro.
Il parametro sync è un flag utile per attivare/disattivare il blocco di recupero del tempo di simbolo che andremo a descrivere più tardi.
Mediante SNRdB impostiamo un desiderato rapporto segnale-rumore, che viene poi tradotto in una data potenza di rumore in relazione alla potenza di segnale.
Con delay possiamo impostare un ritardo in frazioni di simbolo.
Infine f₀ imposta l'offset in frequenza tra il clock di trasmissione e quello di ricezione.

Possiamo quindi generare la sequenza di simboli interi.

seq_sym = np.random.randint(0, 4, N) # valori appartenenti all'insieme {0,1,2,3}
gradi = 45 + seq_sym*90
radianti = gradi*2*np.pi/360.0

Per mezzo della funzione np.random.randint() generiamo una sequenza casuale di N numeri interi i cui valori vengono presi dall'insieme {0,1,2,3}. I simboli vengono poi tradotti in valori di fase espressi in gradi e quindi in radianti.

A questo punto, vengono generati i simboli complessi associati ai simboli interi per mezzo dell'espressione seguente:

x_qpsk = np.cos(radianti) + 1j*np.sin(radianti)

Eseguiamo il sovracampionamento inserendo tra un simbolo e il successivo un numero di campioni nulli pari a SPS - 1.

x_u = np.array([])
for sym in x_qpsk:
  pulse = np.zeros(SPS,np.complex64)
  pulse[0] = sym                                
  x_u = np.concatenate((x_u, pulse)) # add 8 campioni al segnale

Attraverso questo blocco di codice stiamo associando ad ogni simbolo un impulso lungo SPS campioni. Il primo campione di ogni impulso assume il valore complesso del simbolo, mentre i restanti campioni valgono zero.

Ogni impulso può adesso essere dato in ingresso al filtro RRC affinché ne modelli la forma. Il filtro RRC viene definito dal seguente blocco di codice.

num_taps = 101
beta = 0.35
Ts = SPS 
h = rrcosfilter(num_taps, beta, Ts, 1)[1]

La funzione rrcosfilter() appartiene al pacchetto Commpy. Grazie ad essa, possiamo generare un filtro con risposta impulsiva del tipo radice del coseno rialzato (RRC). Il parametro num_taps definisce la lunghezza del filtro in campioni. Il parametro beta è il fattore di roll-off. Mentre gli ultimi due parametri sono rispettivamente il periodo di simbolo (Ts) in secondi e la frequenza di campionamento in Hz. La funzione restituisce due array, di cui ci interessa solo il secondo, ovvero la risposta impulsiva.

Attraverso la funzione di convoluzione np.convolve() andiamo ad imprimere la forma della risposta impulsiva h del filtro RRC agli impulsi rettangolari x_u.

x_shaped = np.convolve(x_u,h)

Possiamo quindi visualizzare i vari segnali che abbiamo generato fino ad ora, grazie al seguente codice.

# plot forme d'onda
plt.figure(0)
plt.subplot(2,2,1)
plt.title('simboli interi')
plt.plot(seq,'.-')
plt.subplot(2,2,3)
plt.title('simboli complessi')
plt.plot(np.real(x_qpsk),'.-')
plt.plot(np.imag(x_qpsk),'.-') 
plt.subplot(2,2,2)
plt.title('impulsi rettangolari')
plt.plot(np.real(x_u),'.-' )
plt.plot(np.imag(x_u),'.-' )
plt.subplot(2,2,4)
plt.title('impulsi RRC')
plt.plot(np.real(x_shaped),'.-')
plt.plot(np.imag(x_shaped),'.-')

In Figura 2 vengono riportati i grafici ottenuti grazie alle funzioni offerte dalla libreria matplotlib.

[...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2915 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.