
Ricordate i vecchi quaderni di scuola, in ultima pagina era riportata una griglia contenente alcuni numeri disposti in ordine crescente e dall'apparenza avvolti da un velo di mistero. Si trattava della Tavola Pitagorica, una raccolta ordinata ed organizzata di tabelline che, utilizzata in modo opportuno, poteva aiutare magicamente ad eseguire calcoli anche molto complessi. In alcune scuole il suo utilizzo era addirittura vietato poiché essa veniva considerata alla stessa stregua della moderna calcolatrice di oggi. Vediamone un po' le caratteristiche salienti ed esploriamo i suoi segreti, al fine di conoscere alcuni lati alternativi della Matematica.
Introduzione
Si tratta di una matrice bidimensionale in cui ogni cella contiene la moltiplicazione dell'elemento x per l'elemento y. La figura 1 mostra una Tavola Pitagorica generica.
A prima vista la tavola permetterebbe di eseguire la semplice moltiplicazione da 1 a 10, ovvero il calcolo delle tabelline che si studiano a scuola. Ma non è così: essa nasconde alcuni trucchi molto interessanti. L'articolo cerca di esaminarne il numero più alto possibile. Una caratteristica che salta subito all'occhio è che la diagonale maggiore, che va dalla posizione in alto a sinistra verso il basso a destra, contiene i quadrati perfetti dei numeri crescenti (1, 4, 9, 16, ecc). Di segreti ve ne sono tanti altri e li scopriremo nel proseguo dell'articolo.
Tabelline
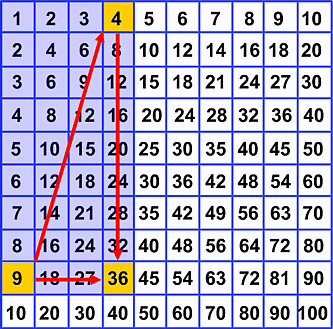
Come detto prima, il calcolo delle tabelline è quello fondamentale e principale e permette, appunto, di ripassare le moltiplicazioni e i prodotti più famosi che si studiano a scuola. Se, ad esempio, si vuol conoscere il risultato della moltiplicazione:
9x4
basta intersecare il 9, posto sulla colonna più a sinistra con il 4, posto sulla riga superiore, come mostrato in figura 2. Si ottiene, ovviamente, lo stesso risultato invertendo le due dimensioni (4x9).
Il prodotto, come si vede dalla illustrazione, è 36. Con lo stesso criterio è possibile ricavare tutte le altre tabelline, dall'uno al dieci. E le sorprese, ovviamente, non si fermano qui.
Somma centrale
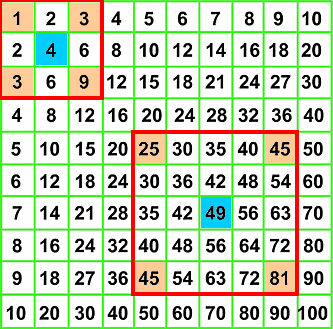
Si disegni un qualsiasi quadrato sulla tavola pitagorica, dal lato composto da un numero dispari di caselle. La somma delle celle situate ai vertici del quadrato corrisponde sempre al quadruplo del numero posto al centro della figura 3. Provare per credere. Nella illustrazione 3, ad esempio la somma dei vertici del quadrato piccolo (1+3+3+9) ammonta a 16, proprio quattro volte il valore della cella centrale, di colore azzurro. E relativamente al secondo quadrato, i vertici (25+45+45+81) totalizza un valore di 196, il quadruplo di 49 situato al centro.
Dietro tutte queste proprietà ci stanno molte regole che possono essere facilmente dimostrate. Ci interessa comunque proseguire con altre curiosità, visto l'aspetto ludico dell'articolo.
Somma laterale o di contorno
Questa proprietà è simile alla precedente e afferma che la somma dei numeri che sono situati intorno ad una tavola pitagorica di lato N è uguale a:
S=(N-1)*(N+1)^2
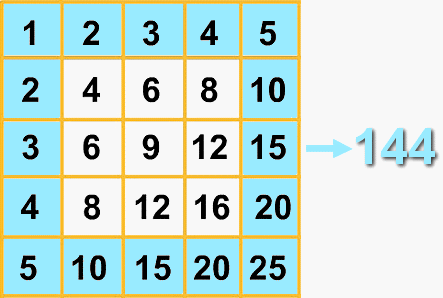
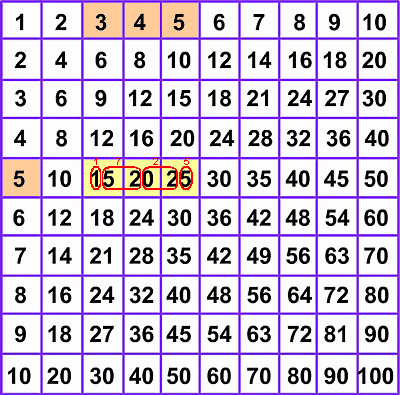
Nella figura 4 è riportata una tavola di ordine 5, nella quale la somma delle caselle che contornano il quadrato ammonta a:
1+2+3+4+5+10+15+20+25+20+15+10+5+4+3+2 = 144
Ebbene, applicando la formula di cui sopra e sostituendo i valori, otteniamo:
S=(5-1)*(5+1)^2
S=4*36=144
Con questo metodo si possono sommare, in un solo istante, i numeri di contorno di tavole pitagoriche immense, composte anche da milioni di caselle. Le caselle intorno ad una tabella composta da un milione di celle per lato darebbe la strepitosa somma di 1.000.000.999.998.999.999.
Somma intorno
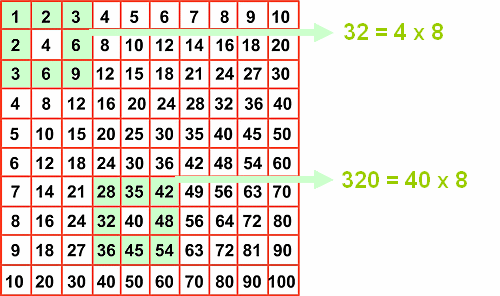
Ci si può sbizzarrire a scoprire da sé alcune proprietà. Per verificare la bontà della scoperta è necessario effettuare tante prove e test sui calcoli oppure realizzare un software ad hoc che esegua il test per ogni possibile evenienza. Questa proprietà, ad esempio, l'ho scoperta io, ma probabilmente esiste già. Essa afferma che la somma di tutte le caselle attorno ad un numero equivale al numero stesso moltiplicato 8. La figura 5 mostra qualche esempio in merito.
Moltiplicazioni a 2 cifre
Sembrerebbe strano ma con la tavola pitagorica è possibile risolvere anche, in maniera semplice, le moltiplicazioni a due cifre. Non è richiesto nemmeno l'utilizzo di fogli di carta, basta utilizzare solo la propria mente. Si debba moltiplicare, ad esempio:
7 x 34
Si focalizzi, pertanto, l'attenzione sul numero 7, posto sulla prima colonna di sinistra, e i numeri 3 e 4 posti sulla prima riga in alto, come mostrato in figura 6. Si può adesso procedere al semplicissimo calcolo nel seguente modo:
- la prima cifra del prodotto è il primo numero della cella che interseca il 7 con il 3, nel nostro caso il 2;
- l'ultima cifra del prodotto è il l'ultimo numero della cella che interseca il 7 con il 4, nel nostro caso l'8;
- La cifra che sta in mezzo al prodotto è la somma tra l'ultima cifra della cella che interseca il 7 con il 3 (1) con la prima cifra della cella che interseca il 7 con il 4 (2), quindi nel nostro caso il 3. Se tale numero dovesse superare dieci, si prende solo l'unità e si aumenta di uno la prima cifra di sinistra del prodotto finale.
- Il prodotto, quindi ammonta a 238.
Il metodo è molto semplice e occorre meno tempo a farlo che a dirlo. La figura sottostante chiarisce ogni dubbio. Provate ad eseguire da soli altre tipologie di moltiplicazioni, vedrete che poi non è così difficile.
Non è necessario che le cifre del moltiplicatore siano consecutive tra loro, come il numero 34. Possono anche trovarsi a distanza tra loro. Con un po' di pratica e di allenamento queste tipologie di operazioni saranno eseguite in pochi secondi.
Moltiplicazione a 3 cifre
Con la stessa tecnica esposta sopra è possibile eseguire addirittura le moltiplicazioni a 3 cifre (e anche di più). Il metodo è sempre il medesimo, basta estenderlo per i numeri successivi. Si debba eseguire, ad esempio, la seguente moltiplicazione:
5 x 345
Il metodo è il seguente:
- Per la prima cifra si prende il primo numero della cella che interseca il 5 con il 3, nel nostro caso 1;
- Per l'ultima cifra si prende l'ultimo numero della cella che interseca il 5 con il 5, nel nostro caso 5;
- Per la seconda cifra si somma il secondo numero della cella che interseca il 5 e il 3 (5) con il primo numero della cella che interseca il 5 con il 4 (2), nel nostro caso 5+2=7;
- Per la terza cifra si somma il secondo numero della cella che interseca il 5 e il 4 (0) con il primo numero della cella che interseca il 5 con il 5 (2), nel nostro caso 0+2=2;
- Il prodotto finale, dunque, è 1725.
La figura 7 illustra con molta chiarezza il metodo, per il quale occorre un po' di allenamento in più rispetto al precedente. Anche in questo caso, se compaiono dei riporti, occorre sommarli alle cifre situate più a sinistra. Con questa tecnica è possibile eseguire moltiplicazioni con numeri composte da tante cifre. Non è necessario che le cifre del moltiplicatore siano consecutive tra loro e con un po' di pratica è possibile utilizzare qualunque numero come moltiplicatore.
Numeri quadrati
Si tratta di una interessante proprietà della tavola pitagorica che può riassumersi nel seguente modo:
"La somma dei numeri contenuti in una porzione quadrata della tavola è un numero quadrato se la casella centrale (o la somma delle caselle centrali) è anch'essa un quadrato".
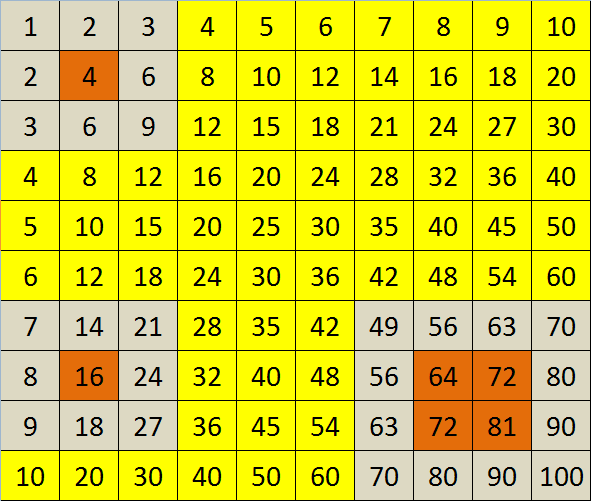
Possiamo verificare subito quanto affermato con alcuni esempi, proposti in figura 8.
Nel primo quadrato, in alto a sinistra, la somma di tutti i numeri in esso contenuto ammonta a 36 (1+2+3+2+4+6+3+6+9). Tale somma è un quadrato (36=6x6) poiché la cifra centrale (4, in colore arancio) è anch'essa un quadrato (2x2).
Nel secondo quadrato, in basso a sinistra, la somma di tutti i numeri in esso contenuto ammonta a 144 (7+4+21+8+16+24+9+18+27). Tale somma è un quadrato (144=12x12) poiché la cifra centrale (16, in colore arancio) è anch'essa un quadrato (4x4).
Nel terzo quadrato, in basso a destra, la somma di tutti i numeri in esso contenuto ammonta a 1156 (49+56+63+70+56+64+72+80+63+72+81+90+70+80+90+100). Tale somma è un quadrato (1156=34x34) poiché la somma delle quattro cifre centrali (64+72+72+81, in colore arancio) è anch'essa un quadrato (289=17x17). Questa evenienza accade se il lato del quadrato è, ovviamente, composto da un numero pari di caselle.
Naturalmente non basta localizzare qualsiasi quadrato per ottenere tale particolarità, ma si deve verificare la specifica condizione esposta prima.
Divisione semplice
Con questo metodo è possibile eseguire le divisioni tra un dividendo, composto da 2 cifre, e un divisore composto da 1 cifra. Si utilizza la tabella in maniera speculare, rispetto a quanto visto fino ad ora. Questa tecnica consente di ottenere il quoto e il resto di una divisione. Un esempio, al solito, chiarirà subito il concetto. Si debba effettuare la seguente divisione:
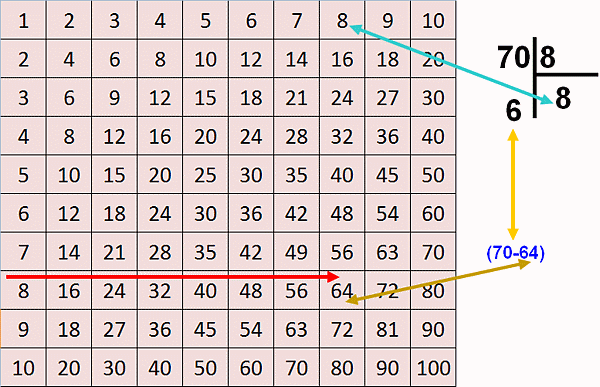
70:8
Il metodo è semplicissimo. Dal momento che il divisore è 8, focalizzeremo la nostra attenzione esclusivamente sull'ottava riga. Si cerchi, pertanto, il numero non superiore al 70, procedendo da sinistra verso destra. La colonna su cui ci si ferma corrisponde al quoziente, mentre il resto è dato dalla differenza tra il contenuto della cella di destinazione e il dividendo. La figura 9 mostra tale operazione di divisione, nella quale il quoto è 8 (8ª colonna) e il resto è 6 (70-64).
Ovviamente, se la cella di destinazione corrisponde al dividendo, non vi è resto e la divisione è intera.
I prodotti uguali delle diagonali
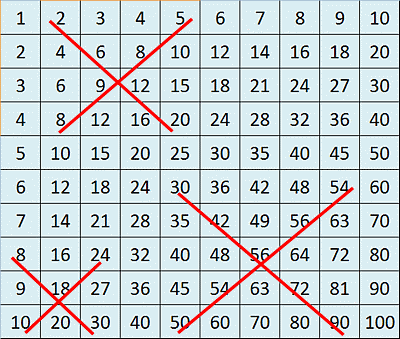
In una tavola pitagorica, i prodotti delle due diagonali di qualsiasi porzione quadrata sono uguali. La figura 10 mostra un esempio contenente più delimitazioni quadrate che mostrano la validità di tale proprietà. Le prime due diagonali, in alto, producono i seguenti due prodotti:
- 2*6*12*20=2880
- 5*8*9*8=2880
Le seconde due diagonali, in basso a sinistra, producono i seguenti prodotti:
- 8*18*30=4320
- 24*18*10=4320
Le terze due diagonali, poste in basso a destra, producono i seguenti prodotti:
- 90*72*56*42*30=457.228.800
- 54*56*56*54*50=457.228.800
Magari l'utilità di tutte queste caratteristiche non balza subito all'occhio ma a chi lavora con le matrici, in programmazione, spesso tali tecniche potrebbero far risparmiare tanto tempo prezioso e codice sorgente.
E adesso... si gioca
Con la tavola pitagorica si possono trascorrere piacevoli e divertenti serate con gli amici, ovviamente amanti della matematica e dei numeri. Un passatempo molto simpatico è il seguente: si ha a disposizione una tavola pitagorica di 10x10 (se si disegna più grande ancora il gioco risulterà ancor più complicato e attraente). Si può disegnare o stampare il tutto su un grande foglio di carta e incollarlo su una tavoletta di legno. Si crei anche una finestrella di dimensioni 2x2 caselle, di plastica o di cartone, in modo che, attraverso essa, si vedano quattro caselle del tabellone. Lo scopo del gioco (vedi figura 11) è quello di posizionare la finestrella sopra quattro caselle, la cui somma dia un numero prefissato (ad esempio 85). Vince chi trova per primo le quattro caselle. Il numero da formare può essere estratto a sorte o deciso da un giudice, quest'ultima è la scelta consigliata per evitare di generare numeri impossibile da costruire con le addizioni.
Creazione della tavola pitagorica in linguaggio C
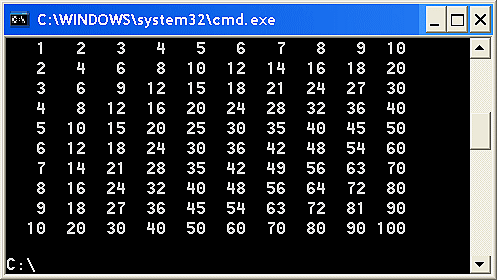
Proponiamo un brevissimo algoritmo, in linguaggio C, che ha lo scopo di mostrare a video una tavola pitagorica dalle dimensioni di 10x10 celle. Il listato, molto semplice, prevede due cicli "for" nidificati, all'interno dei quali avviene il calcolo della singola cella e relativa visualizzazione. Non è necessaria l'adozione di alcuna matrice, poiché i dati non sono memorizzati in modo permanente ma mostrati sul monitor "al momento". Per creare una tabella più grande (o più piccola) è sufficiente impostare la costante "10" ad un valore diverso. La figura 12 mostra l'output a video.
#include <stdio.h>
int main(){
int x,y;
for(y=1;y<=10;y++){
for(x=1;x<=10;x++)
printf("%4d",y*x);
printf("\n");
}
return 0;
}
Esistono tavole pitagoriche contenenti anche le operazioni di addizione, sottrazione e divisione, oltre che a moltiplicazione. Per la loro generazione è sufficiente cambiare l'operatore aritmetico. Si può utilizzare anche il Raspberry Pi per creare il programma.
Conclusioni
La tavola pitagorica offre tanti spunti per sperimentare con i numeri, anche a chi non è molto ferrato in matematica. La sua elasticità, infatti, permette allo sperimentatore di trovare facilmente teoremi e proprietà di qualsiasi genere. L'estensione della tavola non deve essere necessariamente limitata a 10 righe per 10 colonne ma può essere estesa o ridotta secondo le proprie esigenze. L'importante è rispettarne i criteri di costruzione.
L'articolo ha trattato solo una quantità limitata di proprietà e di formule della tavola, in modo tale da non annoiare il lettore, ma vi assicuro che i trucchi e i segreti in essa celati sono davvero tanti.
La filosofia della tavola pitagorica è quella di aumentare l'utilizzo della propria mente, senza alcun ausilio di calcolatori meccanici o elettronici. Gli antichi, infatti, riuscivano ad eseguire complessi calcoli matematici utilizzando questo prezioso mezzo.
Pertanto, d'ora in avanti, nel vostro borsello, portate con voi anche una piccola tavola pitagorica, vi potrebbe servire anche per stupire i vostri amici.
Mi congedo con una domanda: quale è la cifra più frequente (0-9) in una tavola pitagorica 10x10?









E’ come usare in un certo senso il regolo calcolatore, anche se diverso, con uno studio approfondito penso si possano creare delle tabelle con le operazioni possibili per poi applicarle nella reatà lavorativa
Articolo veramente molto interessante. Andrebbe proposto agli studenti che di solito non amano (o non trovano motivi per amare) questa disciplina.
Un’altra proprietà che ho trovato è la seguente:
– Ogni numero è uguale alla media aritmetica della somma dei K numeri che lo seguono e lo precedono, nella sua stessa riga o nella sua stessa colonna. –
Per quanto riguarda la domanda su quale cifra sia più frequente.. a naso direi lo 0 visto che il 100 ne ha ben 2 😉 .. ma magari sbaglio, sono andato a intuito.
La tanto amata e disputata tavola pitagorica , le tabelline vecchi ricordi della scuola, certo conoscerla bene si arriva a questo risultati, che iniziando da me, non ci sarei arrivato. Un semplice esempio che mi viene in mente, il famoso gioco matematico Sudoku, che tutti conosciamo, in quadrato 9×9, la somma dei numero interni deve dare sempre 9, comunque siamo inseriti. si la matematica non è il forte di tutti, bisogna amarla per poterla conoscere al meglio, ed oggi con tutte le tecnologie disponibile è indispensabile, calcoli che ci portano sulla Luna e al quantitativo, veramente straordinario.
Articolo interessantissimo, anche io sono appassionato di matematica. Quando andavo alle elementari usavo molto la tavola pitagorica, stampata nell’ultima pagina dei quaderni a quadri. Poi ho imparato bene le tabelline e non l’ho usata più. Se sapevo che si potesse usare come calcolatrice mi sarebbe stata molto utile anche in seguito, facilitandomi lo studio. Se a scuola insegnassero queste cose, come fanno in India che insegnano i metodi della matematica vedica, si potrebbe imparare molto più velocemente, ma non so perché, a scuola questi segreti non li insegnano. Per quanto riguarda la domanda anche io dico lo 0, c’è ne sono ben 27.
Sono pienamente d’accordo con l’amico Tony21, infatti nelle scuole non danno molto peso a questi particolari importantissimi, l’alunno apprenderebbe meglio, sarebbe quasi come un gioco e lo varrebbe subito suo, e da qui l’entusiasmo per la matematica!
Si potrebbe approfondire l’articolo con la tavola pitagorica cubica, non riesco ad immaginare come realizzarla e come usarla, ma sarebbe molto interessante capirlo. Inoltre si potrebberero fare calcoli complicati.
Articolo molto interessante e completo. Mi è piaciuta in particolare la possibilità di usare la tavola pitagorica per effettuare moltiplicazioni e divisioni a due (e tre) cifre. Ed è un vero peccato che a scuola non insegnino questi giochetti semplicissimi.