
L'argomento crittografia affascina e spaventa sempre, un po' perché ci si perde tra i termini e un po' perché è pensato per non essere semplice, altrimenti i nostri conti bancari sarebbero a rischio perenne. Il termine inoltre fa quasi sempre pensare alle cripto-valute, argomento già trattato in questo articolo dal punto di vista della crittografia. Considerando il numero di attacchi da parte degli hacker e il numero di criptovalute rubate, ci si potrebbe chiedere se davvero gli algoritmi dietro questa tecnologia siano stati studiati con attenzione. La verità è chiaramente un'altra: gli algoritmi sono stati studiati con cura, ma anche i siti di phishing. Molte persone infatti si affidano a siti che promettono di generare wallet (portafogli di criptovalute) sicuri, quando in realtà non sono altro che siti che aspettano che il malcapitato versi liquidità. In questo articolo vedremo passo passo come generare un wallet ad alto livello di sicurezza affidandosi a carta e penna con l'ausilio della matematica.
In principio era la chiave privata
Parlando di crittografia non si può non parlare di chiavi private, pubbliche e curve ellittiche. Qualora il lettore abbia voglia di ripassare, in questo articolo viene illustrata la teoria che vi sta dietro. Per aprire un wallet bitcoin è necessario disporre di una chiave privata, si può considerare come la password per il vostro wallet, colei che vi permetterà di inviare bitcoin e confermare le transazioni. Se siete persone malfidenti, come è giusto che sia in questi casi, deciderete di generare la chiave privata nel vostro bunker affidandovi ad una moneta e un foglio su cui scrivere. Se invece preferite affidarvi ad un servizio online, vi sono molti wallet sicuri. Una panoramica completa si trova a questo indirizzo. Ora si illustreranno i passaggi da seguire per ottenere un wallet affidandosi a metodi offline. La chiave privata di un wallet è composta da 256 bit, per generarne una quindi si lancerà 256 volte una moneta, si farà corrispondere a testa 1 e a croce lo 0 binario e ogni risultato verrà annotato.
Per la trattazione in questione simulando 256 lanci si ottiene:
0100 1100 0011 1111 0101 1110 0101 1001 1001 0010 1101 0010 1000 0110 0101 1111 0100 0000 1101 0101 0101 0001 1001 0101 1110 0101 0001 1101 0010 1100 0011 1010 0001 0101 1010 0001 1101 0101 1010 0100 1101 0101 0101 1100 0101 1010 0000 1101 1110 0010 1010 0101 0101 0010 1101 0001 1010 0001 0010 0000 1010 1111 0101 0101
I vari lanci sono stati raggruppati in 4 bit per semplificare la traduzione in codice esadecimale, infatti utilizzando la seguente tabella è possibile semplificare la rappresentazione della chiave privata.
| Codice binario | Codice esadecimale |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Dopo la conversione la chiave privata è effettivamente più compatta
4c3f5e5992d2865f40d55195e51d2c3a15a1d5a4d55c5a0de2a552d1a120af55
Ora potrebbe esserci il dubbio, giustamente, che generando chiavi private casuali, sia possibile ottenere una chiave effettivamente appartenente ad un wallet. Il dubbio ha ragione di esistere ma il numero di combinazioni possibili è così elevato che richiederebbe uno sforzo infinito trovare un wallet già utilizzato. Esistono più chiavi private possibili che atomi nell'universo. Questa sicurezza è garantita se la chiave è stata generata davvero casualmente. Scegliendo ad esempio una chiave privata come la seguente, si scoprirà che è una chiave così banale che effettivamente appartiene ad un conto che viene puntualmente svuotato.
0000000000000000000000000000000000000000000000000000000000000001
L'indirizzo bitcoin associato è 1EHNa6Q4Jz2uvNExL497mE43ikXhwF6kZm.
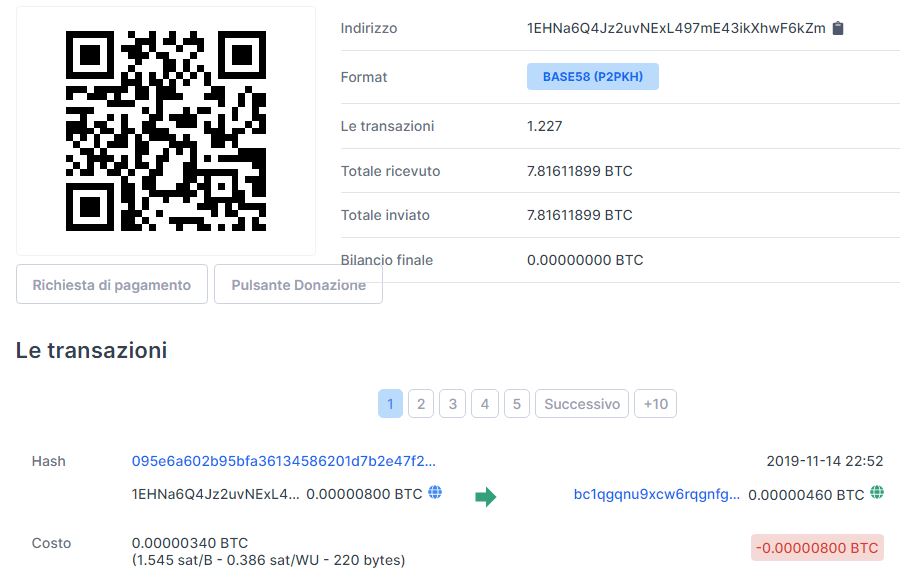
Figura 1. L'indirizzo bitcoin associato alla chiave primaria "banale" ha ricevuto un totale di 7 bitcoin in piccole transazioni, ma viene svuotato appena viene ricaricato
In Figura 1 si illustra la schermata di blockchain.com, essendo la blockchain pubblica è possibile infatti vedere le transazioni effettuate da ogni wallet. Una volta terminato di generare il wallet, si verificherà sulla blockchain se appartiene già a qualcuno.
E poi fu la chiave pubblica
Prima di poter generare l'indirizzo bitcoin associato alla chiave privata, è necessario calcolare la chiave pubblica. La chiave pubblica di un wallet corrisponde alle coordinate del punto sulla curva ellittica Secp256k1, la curva di equazione y2=x3+7.
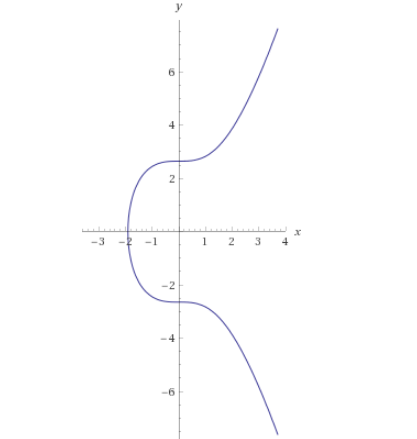
Figura 2. La rappresentazione grafica della curva ellittica, operazione di somma e prodotto all'interno di questa curva vengono definite con le tangenti e le simmetrie ai punti di partenza
In Figura 2 è illustrata la curva in ellittica definita su RxR in cui giacerà la chiava pubblica. La rappresentazione reale dovrebbe essere un insieme di punti in quanto non è possibile avere chiavi pubbliche con la virgola. Per cui solo i punti interi a 32 bit per coordinata vanno bene come chiave. Prima di capire il metodo si ripasserà insieme l'aritmetica dietro l'ellittica.
Somma
In che modo avviene la somma tra due punti sull'ellittica? Si prende in considerazione la retta passante per i punti da sommare. L'intersezione tra la retta e l'ellittica è il punto che rappresenta il risultato dell'opposto della somma. Il risultato quindi è il punto simmetrico rispetto all'asse x.
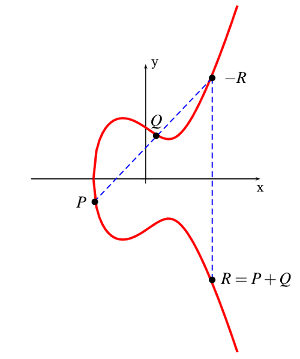
Figura 3. Visualizzazione grafica della somma tra due punti sulla curva ellittica
Considerando la Figura 3, si esegue la somma tra il punto P e il punto Q, la retta incontra l'ellittica sul punto -R, a questo punto si trova il punto simmetrico R, questo è il risultato della somma. Si può inoltre osservare dalla Figura 3 che la somma di due punti opposti non ha alcuna intersezione con la ellittica, per cui si considera che vi sia un punto all'infinito corrispondente allo zero.
La moltiplicazione per due
Moltiplicare per due equivale a sommare lo stesso numero per se stesso, quando si parla di punti sulla ellittica, quindi si tratta di prendere la retta passante per i due punti da sommare. In questo caso i due punti sono coincidenti quindi si tratta di una retta tangente al punto di partenza. A questo punto l'intersezione con l'ellittica sarà l'opposto del risultato.
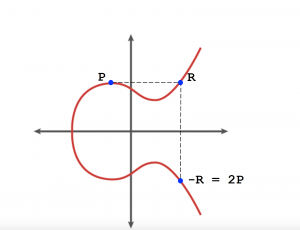
Figura 4. La moltiplicazione per due si sviluppa considerando la tangente al punto di partenza
In Figura 4 partendo dal punto P si ottiene il punto -R che rappresenta 2P. Ora che si sono chiarite le idee su somma e duplicazione, si può, partendo da un punto, moltiplicarlo per qualunque numero. Il prodotto di un punto dell'ellittica x5 per esempio si realizzerà come ((P*2)*2)+P. Per cui si disegneranno due tangenti per ottenere 4P e infine la retta passante per il punto appena trovato e P. Quando si tratta di crittografia i numeri in questione sono molto più grandi e il numero di somme e moltiplicazioni decisamente più elevato.
Calcolo chiave pubblica
La chiave pubblica servirà per la generazione dell'indirizzo bitcoin a cui inviare eventuali criptovalute.
Per generare la chiave pubblica [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2027 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.







Ottimo esempio di cooperazione tra crittografia, probabilità e funzioni matematiche: la chiave privata ottenuta grazie ad un semplice algoritmo che genera numeri casuali in binario; la chiave pubblica ricavata da una funzione ellittica. Con questo articolo l’autore, oltre ad illustrare bene gli algoritmi per generare le due chiavi pubbliche e private, ha evidenziato la differenza tra le due e i motivi per cui utilizzarle distintamente.
Ciao Mariangela,
la matematica riesce ad affascinare sempre, la generazione della chiave privata è assai semplice, non lo è altrettanto ricavarla avendo la chiave pubblica per nostra fortuna.
Spero sia stata una lettura piacevole,
un saluto e buona continuazione