L’amplificatore operazionale è senza dubbio uno degli elementi chiave sia nell’elettronica analogica che digitale. È infatti in grado di realizzare il front-end analogico dedito al filtraggio dei segnali utili, avvalendosi di circuiti retroazionati, oppure possiamo utilizzarlo come semplice comparatore per ottenere un DAC. Tuttavia il suo comportamento reale si discosta da quello ideale a seconda del punto di lavoro e della tecnologia (MOS, BJT). Il comportamento varia sia in termini di larghezza di banda che di guadagno. In questo articolo illustreremo le varie non idealità che incontriamo dentro al nostro componente, cercando anche di trovare dei metodi per tenerne conto nei nostri circuiti o simulazioni.
Amplificatore Operazionale
Figura 1: Simbolo circuitale di un op-amp ad alimentazione duale
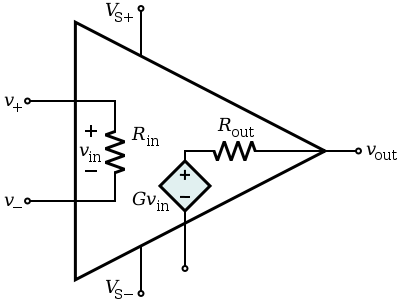
L’amplificatore operazionale ideale è caratterizzato da valori di guadagno, banda e resistenza di ingresso infiniti (Figura 1). Nonostante ciò, il guadagno è sottoposto a delle limitazioni a causa dei componenti interni. In generale un op-amp (amplificatore operazionale) presenta due stadi di guadagno al suo interno che per quanto elevato non sarà mai infinito, specialmente a causa del fatto che all'aumentare del guadagno corrisponde una dissipazione di potenza proporzionalmente elevata, ma ci sarà senz'altro più chiaro quando illustreremo il circuito interno. Le capacità parassite, inoltre, aggiungeranno ognuna un polo riducendo la nostra banda. La tecnologia a transistore bipolare è la migliore da questo punto di vista, in quanto ci assicura capacità parassite più piccole. Le correnti transitanti nei morsetti (+ e -) non potranno essere nulle come nel caso ideale, nemmeno in tecnologia FET, infatti all’interno dell’ossido vi sono delle correnti di leakage dovute all’effetto tunneling, queste aumentano man mano che l’ossido diventa più sottile e considerando il processo di scaling questo fenomeno cresce sempre di più costringendoci a cambiare materiali per l’ossido. Nei BJT, invece, le correnti nella base dei transistor sono parte della polarizzazione di esso, senza contare quelle che si aggiungeranno in presenza di un segnale in ingresso. La tensione di uscita quando in ingresso non vi è applicato alcun segnale è diversa dal valore di riferimento, questo si può prendere in considerazione aggiungendo in ingresso un generatore di tensione di offset, quindi tratteremo lo spostamento della tensione in uscita come se fosse dovuto ad un ingresso aggiuntivo. Per quanto riguarda la resistenza d’uscita, invece, questa tenderà ad essere più piccola possibile, idealmente nulla. Cerchiamo di capire meglio analizzando il circuito interno.
Modello interno e funzionamento
Figura 2: schema circuitale semplificativo di un u741, amplificatore a tecnologia bipolare
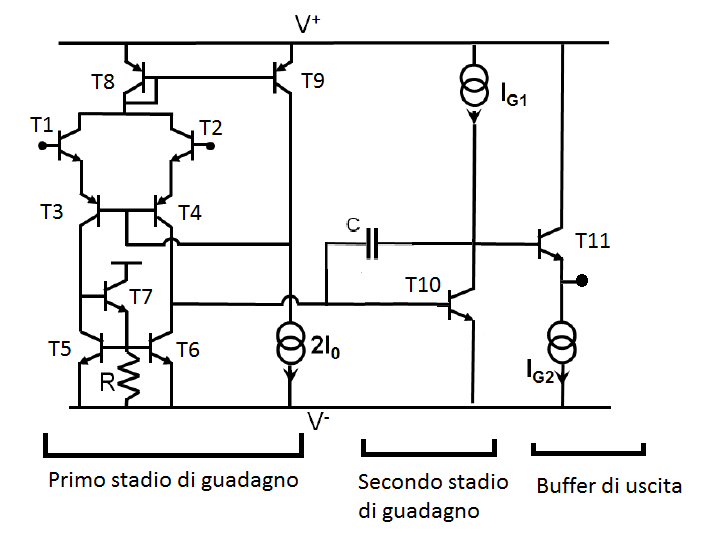
Come si può vedere dalla figura 2, il guadagno complessivo è dato dal prodotto dei guadagni dei due stadi iniziali, potrebbe venire in mente di costruire un op-amp con più stadi per ottenere guadagni altissimi, tuttavia è possibile solo in linea teorica, la ragione risiede nel fatto che ogni stadio aumenta il numero di poli riducendo la banda e abbassando il margine di fase. T1 e T2 saranno i nostri morsetti + e – dell’op-amp (amplificatore operazionale), questo spiega la presenza delle correnti di bias che scorrono dentro la base dei transistor permettendone il funzionamento. La resistenza in ingresso sarà quindi quella delle basi dei transistori T1 e T2, nel nostro caso 4β/gm, che quindi dipenderà sia dalla tecnologia utilizzata, infatti β varia tra BJT di tipo npn o pnp, sia dalla polarizzazione per la presenza di gm a denominatore (gm=2I/Vth) . Il guadagno di ogni stadio è in diretta correlazione esclusivamente con il punto di lavoro dei transistori T1, T2 e T10, per aumentarlo è necessario generare un'elevata gm, ciò è possibile solo incrementando la corrente di polarizzazione (I0 e Ig1), producendo in questo modo una forte dissipazione di potenza. I poli del circuito saranno strettamente connessi ai punti ad alta impedenza, ovvero le uscite degli stadi di guadagno, e di conseguenza alle capacità parassite in quei punti. Compito del designer sarà aggiungere un polo a frequenza più bassa per garantire una corretta stabilità di tutto il sistema, aggiungendo per esempio una capacità di compensazione tra la base di T10 e T11 (come mostrato in figura 2) per sfruttare l’effetto miller. Un altro parametro da considerare è lo slew rate del nostro amplificatore; configurando come ingresso uno scalino di tensione, l’uscita avrà bisogno di un certo tempo per poter assestarsi al valore asintotico. Lo slew rate è la pendenza della curva con cui si raggiunge il valore asintotico, come mostrato in figura 3, dipende linearmente dalla corrente di polarizzazione I0 e aumenta al diminuire della capacità di compensazione.
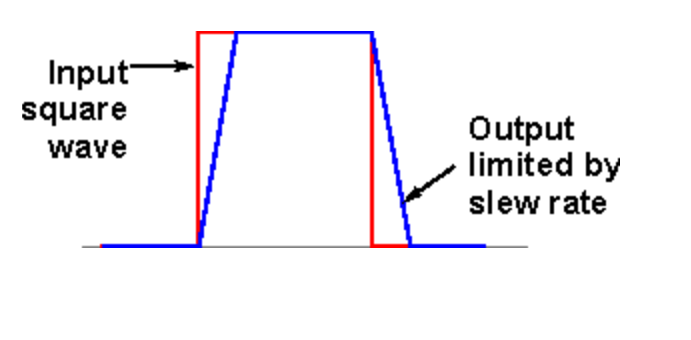
Figura 3: La risposta ad un impulso rettangolare avrà una corrispondente uscita che impiegherà del tempo per assestarsi, il limite è dato dalle correnti di polarizzazione, la pendenza dell'output è lo slew rate
Come uscita troviamo un buffer ideale, la cui resistenza di uscità è 1/gm di T11, che per quanto bassa non sarà mai nulla come nel caso ideale, perché aumentando la gm per diminuire la resistenza di uscita, si rischia di incappare in un calo eccessivo della resistenza equivalente alla base di T11 che comporterebbe una riduzione del guadagno nel secondo stadio; ricordiamo infatti che il guadagno di uno stadio è dato dal prodotto della sua transconduttanza per la resistenza di uscita.
Modelli
Figura 4: Schema circuitale di un op-amp, questo è il modello più semplice e conosciuto
Il modello mostrato in figura 4 è quello che si usa per presentare l’op-amp, semplice e conciso. Tuttavia non basta se si ha intenzione di iniziare ad utilizzarlo in simulazioni o nei propri schemi, bisognerà munirsi di un modello più semplice del caso reale, ma che allo stesso tempo tenga in considerazione il comportamento reale dell’amplificatore, soprattutto in termini di risposta in frequenza. Analizziamo insieme un paio di modelli.
Modello di Boyle
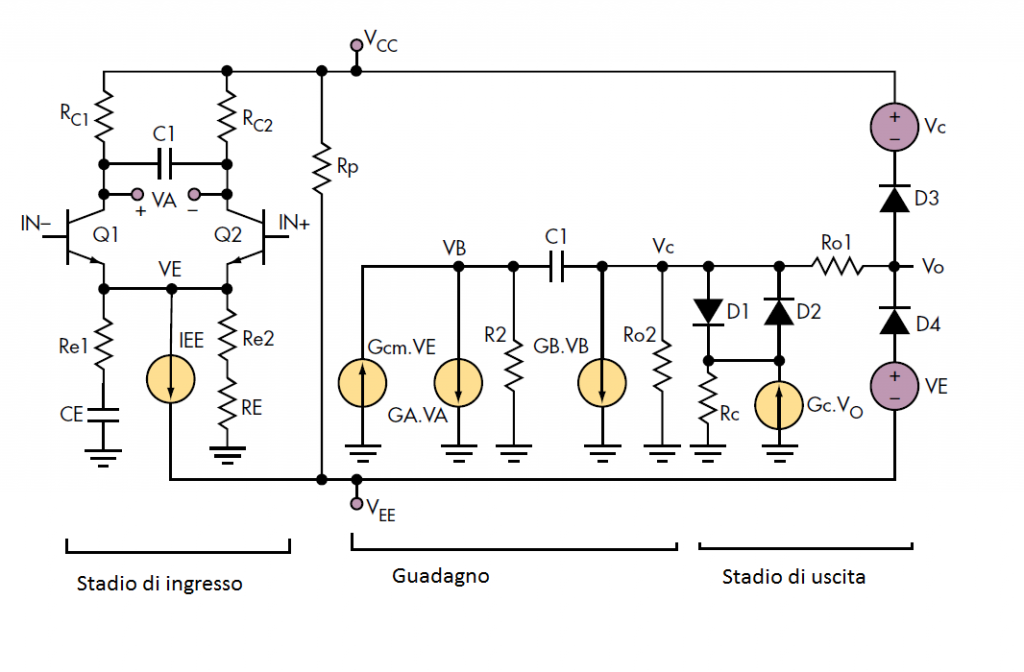
Boyle oltre a realizzare il modello semplice mostrato in figura 5, sviluppò un modello tenendo in considerazione gran parte delle non idealità.
Figura 5: Modello di Boyle, tiene in considerazione molte delle non idealità
L’obiettivo era cercare di ottenere un modello diminuendo il numero di componenti non lineari, gli unici componenti non lineari rimasti sono soltanto i transistori d'ingresso e i diodi utilizzati per fissare le tensioni. Questo modello tiene in considerazione le correnti di bias in ingresso, il CMRR modellizzato dal generatore di corrente Gcm che dipende solo dalla tensione VE, i limiti della tensione di uscita e la resistenza corrispondente di uscita. Per quanto riguarda l’analisi in frequenza invece, tiene in considerazione lo slew rate e la funzione di trasferimento, per quanto riguarda quest’ultima si valutano solo il polo o i poli iniziali. Tuttavia non vengono rappresentati adeguatamente gli effetti della distorsione, dell’offset, dei limiti della tensione in ingresso e il comportamento in frequenza della resistenza di uscita non è sufficientemente adeguato, inoltre gli stadi di guadagno fanno riferimento a massa e questo non è sempre vero all’interno di un op-amp.
Modello di Alexander & Bowers
Figura 6: il modello di Bowers si basa su quello di Boyle migliorando l'analisi in frequenza
Lo schema di figura 6 visualizza il modello di Bowers che rispetto a quello di Boyle è più accurato. In particolare come riferimento non utilizza più massa ma uno interno dipendente dalle alimentazioni. Lo stadio di input è rimasto pressoché uguale, con l’aggiunta dell’offset e della resistenza d’ingresso. Ogni non idealità in questo modello viene rappresentata da un blocco, in cui l’output di uno stadio diventa l’input di quello successivo. È evidente come questo modello si adatti meglio durante l’analisi in frequenza in quanto è possibile aggiungere poli e zeri a piacimento per ottenere una funzione di trasferimento più simile a quella reale. Tuttavia, proprio come nel modello precedente, non viene presa in considerazione [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2566 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.
Ti potrebbe interessare anche:
Come trasferire uno stile pittorico su una fotografia con Python
Progetto di un sistema di allarme di terremoti con Arduino – Parte 3
Progetto di un Data Logger con microSD e microcontrollore ESP32 – Parte 1
Alla scoperta dell’ESP32
Stato dell’arte nella rete 5G
Grazie Raul ,
l’articolo e’ molto approfondito , mi capita spesso di dover utilizzare operazionali nei miei progetti , specie per cio’ che riguarda la gestione di piccoli segnali analogici come i rilevamenti di sensori di corrente o controlli di tensioni ( Comparatori ) o amplificare segnali .
Devo dire che facendo riferimento ai Datasheet corrispondenti e’ molto semplice impiegarli ed il loro collegamento in cascata e’ sicuramente un punto di forza nella progettazione di circuiti che devono manipolare segnali.
Li ho utilizzati nelle piu’ classiche configurazioni di amplificatori invertenti e non , comparatori di tensione e sommatori o inseguitori di corrente , senza riscontare problemi nel comportamento tra modello ideale e reale , dipende dal tipo di applicazione che si deve fare.
Sara’ la gestione finale del segnale che dovra’ tenere conto poi dei parametri di tolleranza , effettuando in fase di test le necessarie correzioni tarando opportunemente eventuali valori di resistenze o capacita’ ,
Saluti
Questa tematica mi ha fatto tornare indietro nel tempo, ai tempi dell’università. Non per niente gli amplificatori operazionali sono componenti fondamentali per buona parte dei circuiti elettronici., specialmente in ambito musicale.
Bravo Raul, ottimo articolo, ad Alessandro lo hai fatto tornare ai tempi del’università… a me addirittura nel lontano 1993, al mio esame di stato al quale ho portato questo splendido amplificatore come oggetto di esame in elettronica e misure… 555 e chi lo dimentica più !
Concordo con Alessandro e Michele: un tuffo nel passato della mia università, dei primi ampli e dei filtri,… con un pizzico di nostalgia. Mi ricorderò sempre come da una formula matematica con qualche derivata, abbiamo convertito i blocchi con operazionali retroazionati, senza considerare alcuna ‘non idealità’ e alla fine siamo riusciti a tenere fermo immobile in coppia un motore DC con una leva e un peso!! e ci ha fruttato un bel voto all’esame di elettronica applicata (1995)!
Grazie Raul!
Grazie a Raul, un po’tutti con la mente, siamo ritornati a scuola alla scoperta del Op. Chi nel suo piccolo non ha avuto l’approccio con questo circuito tanto interessante quanto problematico. Ancora oggi mi ci imbatto facilmente poiché c’è sempre da inserirlo in qualche contesto elettronico, ultimamente ho realizzato un raddrizzatore a due semionde di un segnale alternato di pochi millivolt, e l’Op ha risolto il problema egregiamente. Cosa dire più!
Si può scaricare l’articolo come pdf ??
Ah, quanti ne ho carbonizzati all’università prima di capire come utilizzarli. Il tecnico di laboratorio però si armò di pazienza e oscilloscopio e mi fece capire i miei sbagli. Ora mi piacerebbe mostrare questi gioiellini ai miei alunni di scuola superiore ITT informatica ma con arduino e raspberry non c’è molto tempo purtroppo se non con corsi pomeridiani.
E vero che oggi e l’epoca del digitale, microcontrollori, Arduino Raspberry processori ecc, ma e altrettanto vero che l’analogico e cmq sempre presente, per cui non può essere trascurata, non solo, ma i circuiti amplificatori operazionali vengono usati da per tutto. Per tanto non bisogna abbandonare il loro studio e applicazione da insegnare agli studenti.
Sono d’accordo con Giulio. Aggiungo che la conoscenza di questi componenti non dovrebbe essere limitata solo alla trattazione teorica ma puntare molto sulla simulazione del funzionamento di questi componenti, ad esempio attraverso il PSpice.
Certo Alessandro, ora sono io d’accordo con te non potevi dare idea migliore che l’utilizzo di un sw. Simulatore di circuiti elettronici. Ovviante ve ne sono diversi per lo più a pagamento quelli più completi, ma anche versioni light, per fare un primo approccio a questi sw. Anche per principianti e/o studenti per apprendere ed inserirsi in questo mondo. Che devo aggiungere molto bello, soprattutto a chi impara ad amarlo.
L’amplificatore operazionale è forse l’unico componente analogico che si comporta come un componente ideale (con l’utilizzo dei giusti componenti al contorno le non idealità vengono adeguatamente “gestite”).
Non si tratta di qualcosa che appartiene ai ricordi (ai “vecchi tempi” dell’elettronica analogica”) ma è ancora attuale perché la natura è analogica e quindi in qualunque sistema digitale deve esistere uno stadio di condizionamento dei segnali prima della conversione AD: i filtri, i buffer , ecc. sono realizzati mediante operazionali.