
Utilizzate molto spesso per la risoluzione di problematiche elettroniche complesse, le macchine a stati finiti non occupano importanti spazi nei libri di automazione. Genitrici dei moderni computer, e in grado di svolgere funzioni di qualsiasi tipo, oggi risentono dell’avvento delle moderne tecnologie. In quest’articolo apporteremo un’analisi a questo tipo di dispositivi, cercando di arrivare ad una spiegazione semplice ed esaustiva di un ambiente in evoluzione da più di sessant’anni.
Molto differente da qualsiasi elaboratore, e impiegate nei settori in cui il calcolo regna sovrano, le macchine a stati finiti (MSF), o automi a stati finiti (ASF), sono sistemi sincroni in cui lo stato delle uscite sono frutto dell’interazione degli ingressi con un’opportuna funzione logica sequenziale.
LA VISIONE GLOBALE
Nell’introduzione si è parlato di automa a stati finiti, anche se morfologicamente la parola automa ricorda più la struttura di un robot, nel nostro caso specifico ci si riferisce ad un modello matematico di un sistema con input e output discreti. Il sistema può trovarsi in una configurazione compresa tra n situazioni differenti, dette stati. Lo stato, rappresenta una condizione in cui il sistema si trova, e riassume in se la storia precedente riguardante gli input ricevuti e processati. Si consideri l’esempio in cui un automa debba riconoscere stringhe contenenti la sequenza ’001’. Una condizione possibile per la risoluzione è quella in cui gli ultimi due bit ricevuti siano uguali a zero, implicando la necessità di almeno due bit di memoria. In un automa a stati finiti, la conoscenza dello stato in cui si trova il sistema e’ necessaria per determinare il comportamento a fronte di input successivi. Infatti, a ogni nuovo ingresso, il calcolatore transita in un nuovo stato, e questo è rappresentato graficamente nel modello in figura 1.
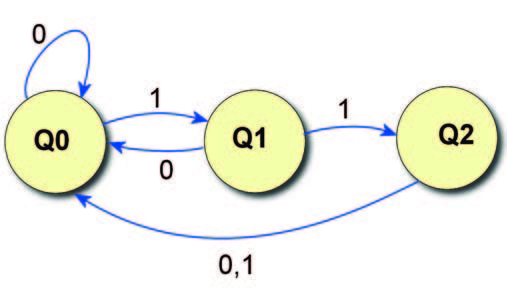
Figura 1: grafico di lavoro di una comune macchina a stati finiti
A fronte di questo preambolo si può generalizzare una definizione come la seguente:
Un automa a stati finiti è una quintupla (Q, Σ, δ , q0, F) dove
- Q è un insieme finito di stati
- Σ è un alfabeto finito di simboli
- q0 è lo stato iniziale
- F Q è il set di stati finali
- δ è la funzione di transizione QxΣ (q,a).
QxΣ è il prodotto cartesiano, ovvero l’insieme delle coppie (q,a), mentre δ (q,a) rappresenta uno stato raggiunto dall’automa, per ogni ogni stato di partenza differente da q0. Una macchina a stati finiti come quella appena descritta, ammette ingressi, ma non una condizione d’uscita. Il comportamento di un circuito sequenziale può essere modellato mediante un particolare tipo di automi a stati finiti: gli automi deterministici con output. Questi ASF vengono rispettivamente chiamate macchine di Moore o di Mealy, a seconda che l’output sia associato agli stati, o alle transizioni fra stati.
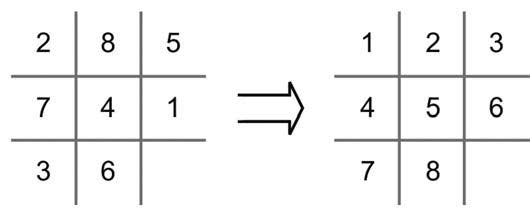
Figura 2: rappresentazione grafica della soluzione del progetto.
La macchina di Melay
La macchina di Mealy è un automa a stati finiti che genera un’uscita a partire dagli stati d’ingresso e del sistema, lavorando solo in funzione dell’andamento corrente. L’MSF di Melay fornisce un rudimentale mezzo per l’implementazione di sistemi cifrati: eseguendo ad una data stringa di lettere (ovvero una sequenza di ingressi) una conversione ad una sequenza cifrata (ossia di uscite). Sebbene sia possibile, ad esempio, descrivere Enigma attraverso una macchina di Mealy, il diagramma degli stati risulterebbe troppo complicato per capire il funzionamento delle macchine cifrate.
Definizione matematica
Una macchina di Mealy è una sestupla, (Q, q0, Σ, Λ, δ, G), costituita da:
- un insieme finito di stati (Q)
- uno stato iniziale q0, che è un elemento di (Q)
- un insieme finito chiamato alfabeto degli ingressi (Σ)
- un insieme finito chiamato alfabeto delle uscite (Λ)
- una funzione di transizione (δ: Q × Σ → Q)
- una funzione uscita (G : Q × Σ → Λ)
La macchina di Moore
La macchina di Moore è un automa a stati finiti in cui lo stato delle uscite dipende solamente dall’andamento della funzione interna alla macchine, e non, come accadeva nella macchina di Mealy, anche dallo stato degli ingressi. Ad ogni cambiamento di stato viene associata un’uscita. La maggior parte dei componenti elettronici digitali vengono progettati come come sistemi sequenziali ad impulsi di clock, che sono una forma ridotta della macchina di Moore, dove lo stato cambia solo quando varia il segnale globale di clock. Generalmente lo stato corrente viene salvato nei flip-flop, mente il segnale globale di clock viene collegato nell’ingresso dei flip-flop riservato al clock.
Definizione matematica
Una macchina di Moore è una sestupla, (Q, q0, Σ, Λ, δ , G), costituita da:
- un insieme finito di stati (Q)
- uno stato iniziale q0, che è un elemento di (Q)
- un insieme finito chiamato alfabeto degli ingressi (Σ)
- un insieme finito chiamato alfabeto delle uscite (Λ)
- una funzione di transizione (δ : Q × Σ → Q) che mappa uno stato ed un ingresso allo stato prossimo
- una funzione uscita (G : Q → Λ) che mappa ciascun stato nell’alfabeto delle uscite.
UNA MSF CON MSP430
Molti sistemi basati su MSP430 sono utilizzati in dispositivi di controllo a logica orientata come: la misurazione, il monitoraggio e il controllo. Una caratteristica che hanno in comune queste applicazioni è che il sistema risente di condizionamenti esterni. Il software di un tale componente si basa essenzialmente sui salti incondizionati e nella manipolazione dei bit. Ci sono molti modi per descrivere l’andamento temporale del software del MSP430: il più semplice consiste nel realizzare una funzione principale e richiamare attraverso apposite procedure le interazioni con le sub-routine. Per lavorare più elegantemente, l’ideale è utilizzare il cosiddetto concetto di macchina a stati finiti: al verificarsi di un evento il sistema reagisce mutando il proprio stato interno, condizionando i livelli delle uscite. L’MSP430, prodotto da Texas Instrument inc., è un microcontrollore 16bit, pensato per essere impiegato come cuore per le macchine a stati finiti.
Una piccola applicazione
Per comprendere come sia facile la realizzazione di un progetto mediante gli strumenti messi a disposizione da TI, si è pensato di realizzare un dispositivo per giocare al gioco del 9. Il gioco consiste in un quadrato suddiviso in 3 righe e 3 colonne, in 8 di queste celle create dalla ripartizione si dispongono a caso i numeri da 1 a 8. Lo scopo del gioco sarà ordinare le celle in numeri consecutivi in modo che: in alto a sinistra compaia il numero 1 e in basso a destra il numero 8. Dal punto di vista di una macchina a stati finiti, questa applicazione definisce nove differenti stati, uno per ogni possibile cella libera (rappresentati nella figura 3 con il nome di “Empty Field 1” a “Empty Field 9”. Si aggiungeranno a ciò le due situazioni: gioco in atto (“Init Game”) e gioco fermo in caso di vittoria (“Stop Game”). Per il movimento della casella libera all’interno della tavola, si troveranno gli eventi: Left, Right, Up e Down, ognuno occupante uno stato.
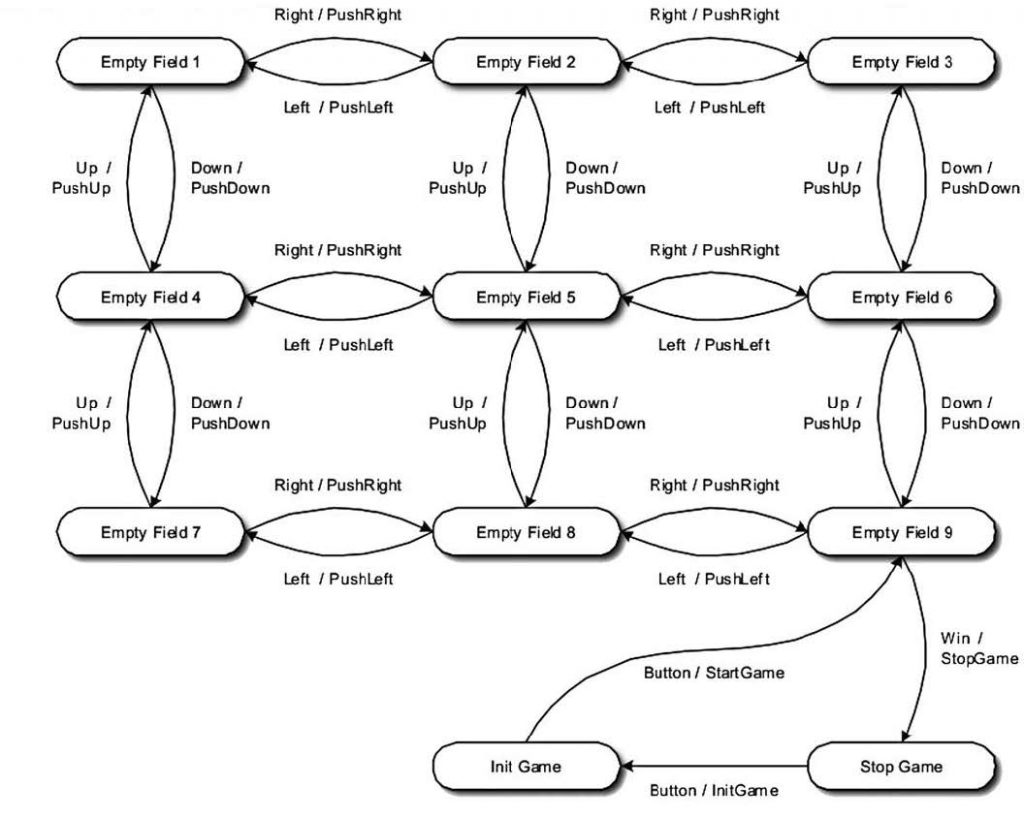
Figura 3: tavola riassuntiva gli stati, e le transizioni da programmare all’interno del microcontrollore.
LA REALIZZAZIONE DEL PROGETTO
L’MSP430 generalmente viene programmato in linguaggio C e compilato attraverso l’apposito ambiente di sviluppo Texas Instruments. Nel caso di implementazione in una macchina a stati finiti, TI rende disponibile nel proprio sito [1] un apposito pacchetto che semplifica il lavoro del programmatore. Dopo aver definito gli stati, e aver creato un apposito schema funzionale come quello in figura 3, il passo successivo è l’utilizzo del FSMGenerator. Ora, aperto l’FSMGenerator.xls con Microsoft Excel e dopo aver abilitato l’utilizzo delle macro, si dovrà provvedere al riempimento della tabella, facendo attenzione ai seguenti punti:
- Definizione degli stati
Il primo passo per il completamento della tabella, e specificare il numero totale di stati che il sistema potrà avere (figura 4a). Il numero totale è limitato a 32, e di default il sistema nominerà ogni stato con l’appellativo di StateN (figura 4b), dove N è un numero consecutivo indicante il numero totale utilizzato fino a quel momento. Il valore più in alto nella tabella corrisponde con il valore di inizio. - Definizione degli eventi
In questa sezione si impostano gli eventi che potranno accadere. Come per gli stati, anche il numero totale degli eventi dovrà essere specificato (figura 4c), raggiungendo ugualmente il valore massimo di 32. - Definizione delle transizioni
Una transizione è il passaggio da uno stato all’altro, la quale avviene solamente in presenza di un evento. Lo stato successivo può essere selezionato dall’apposito menù a tendina, contenente la lista degli eventi disponibili (figura 4e). Ogni transizione necessita di essere definita, in caso ciò non accadesse avverrà una situazione di loop back, in cui lo stato rimarrà il medesimo.
- Definizione delle azioni
Ad ogni cambiamento di stato coincide un’azione, ivi per cui nel campo apposito (figura 4f) si dovrà specificare l’eventuale azione da eseguire.
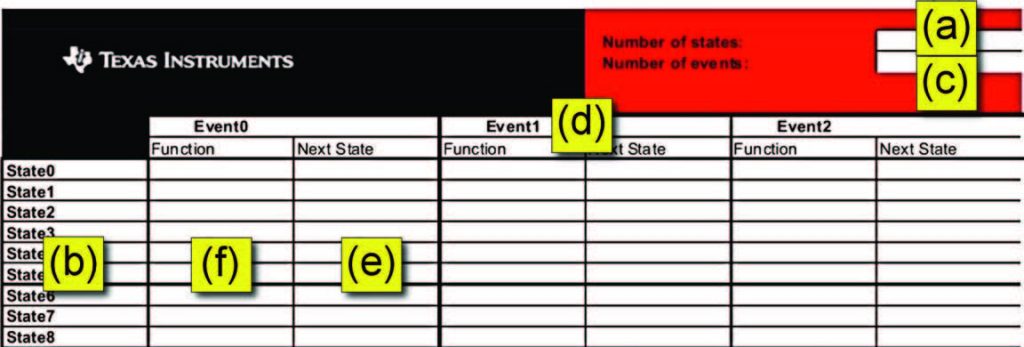
Figura 4: ambiente per la creazione del codice C partendo dalla tavola degli stati e degli eventi.
La generazione del codice
Completata la tabella, l’FSMGenerator dispone dell’apposito pulsante di generazione del codice, non appena premuto, nella cartella in cui è in esecuzione il file Excel verranno automaticamente resi disponibili tre file:
fsm.c
Questo file contiene le informazioni dichiarate nella tavola delle funzioni, e corrisponde alla lista degli eventi precedentemente descritti. È consigliabile non modificare le informazioni al suo interno.
fsm_transition.c
Per ogni transizione descritta nella tavola precedente, viene generata una funzione. Ogni funzione di transizione viene salvata all’interno di questo file.
fsm.h
Questo file contiene l’intestazione standard per la realizzazione di macchine a stati finiti, è la parte del programma che trasforma l’MSP430 in una vera e propria MSF.
La simulazione
Nella fase finale della progettazione di un sistema troviamo la simulazione. Purtroppo in questo caso non sarà possibile eseguire il circuito virtualmente, tramite una perfierica software, ma si dovrà sfruttare l’ambiente di sviluppo MSP-EXP430F5438 disponibile nel sito TI. Caricato il file IAR e il CCE, e compilato il codice C, la dimostrazione del funzionamento sarà visibile direttamente nel circuito.
CONCLUSIONI
Le macchine a stati finiti hanno gettato le fondamenta per la realizzazione dei moderni sistemi automatici, cominciano ad essere datate, ma con l’avvento di tecnologie nuove e versatili riescono in ogni caso a mantenere il proprio posto nel mondo dell’elettronica. Sono conscio che questo breve articolo possa solo fornire un’infarinatura generale riguardante le MSF, ma in ogni caso, con gli strumenti messi a disposizione da Texas Instruments Inc., chiunque, con competenza in materia, riuscirà facilmente a realizzare il proprio progetto.




Apparentemente le macchine a stati finiti potrebbero sembrare un argomento di nicchia. Nella realtà sono dotate di un’elevata capacità computazionale, al punto da essere state i precursori dei moderni computer e sistemi automatici.
Sarebbe interessante investigare su nuovi impieghi delle macchine a stati finiti, in particolare in quegli ambiti dove esse potrebbero rendersi competitive. Ad esempio tutto ciò che riguarda la modifica di una macchina a stati finiti, risulta in genere molto semplice: aggiungere o rimuovere uno stato infatti è una operazione molto semplice perché si riduce a modificare le transizioni che riguardano lo stato aggiunto o rimosso senza alterare il resto del progetto.
Le macchine a stati finiti, per brevità FSM, sono spesso implementate nei codici software e nei firmware dei microcontrollori, ivi compreso Arduino, con costrutti ad alto livello del tipo switch-case. Un’applicazione tipica è la gestione dei menù di selezione a schermo, dove l’avanzamento delle voci avviene interagendo ad esempio con la manopola di un encoder incrementale o più semplicemente tramite dei tasti up e down. Se ogni singola voce di menù è vista come un possibile stato e gli impulsi di up e down come ingressi, ecco che si riconosce la struttura di una FSM come descritta nell’articolo.
Di tool tipo FSMGenerator messo a disposizione dalla TI in rete se ne trovano di diversi, per tutti i tipi di microcontrollore. Ad esempio, l’implementazione semplificata di una FSM su Arduino si può sviluppare tramite il tool YAKINDU (scaricabile gratuitamente nella versione per maker) che propone una programmazione a diagrammi di stati come siamo abituati a progettare una FSM carta e penna, altrimenti esistono librerie open source come https://github.com/jonblack/arduino-fsm che, opportunamente richiamate ed istanziate nel codice, semplificano la creazione degli stati e le transazioni controllate tra gli stessi.
Sulle FSM si strutturano inoltre i sistemi operativi e, restando sui sistemi embedded e a micrcontrollore, anche i RTOS, il più famoso dei quali è proprio il Free-RTOS.
Lavoro nel settore automotive per un’azienda italo-giapponese che fa centraline. Vi posso dire che le macchine a stati finiti sono il pane di ogni giorno. Al giorno d’oggi, per sviluppare il SW, si utilizzano tools ad alto livello tipo Matlab Simulink/Stateflow che permettono di creare gli algoritmi di controllo in maniera piu’ semplice. Poi, e’ possibile generare codice C a partire dai modelli Simulink/Stateflow (macchine a stati), Matlab dispone di una funzionalita’ di nome “Autocode”. E infine, si integrano i moduli creati in maniera automatica e quelli creati con codice a mano, e si compila.
Nell’ambiente automotive (e penso in generale per qualunque sistema di controllo complesso, inclusi aerospace etc.) le macchine a stati sono utilizzate moltissimo, per modellare i vari stati in cui puo’ trovarsi un sistema, e definire azioni diverse a seconda dello stato.
Esempio: veicolo fermo allo stop, veicolo decelerazione, veicolo a velocita’ costante, etc.