I numeri primi hanno sempre esercitato un grande fascino per i matematici e per l’umanità intera. Protagonisti di film e best seller letterari, hanno stimolato la fantasia di milioni di persone. Ma cosa sono i numeri primi? Chi li ha scoperti? Vediamo insieme i concetti principali legati a questi numeri particolari e l’uso che ne è stato fatto, per esempio nell’ambito della crittografia.
Cosa sono i numeri primi
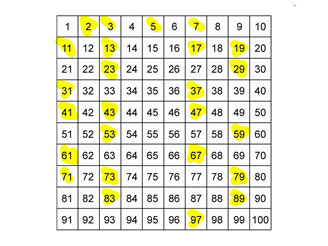
Un numero primo è un numero intero e positivo (cioè un numero naturale) maggiore di 1 che può essere diviso solo per 1 e per se stesso. Per esempio, 2, 3, 5 e 7 sono numeri primi, mentre 4 non lo è perché è divisibile anche per 2. L'unico numero primo che è anche pari è il numero 2, in quanto ovviamente tutti gli altri numeri pari sono divisibili come minimo anche per 2. In passato anche l’1 veniva considerato da molti un numero primo, sebbene si trattasse di un caso particolare. Oggi si tende ad escluderlo, perché considerarlo un numero primo costringerebbe a riformulare in modo molto complicato diversi teoremi che riguardano i numeri primi.
I numeri primi sono stati studiati sin dall'antichità, anche se non si sa con certezza quando sia stata formulata la prima teoria al riguardo. Il primo reperto che potrebbe essere collegato ai numeri primi è l’osso di Ishango, dove ci sono dei segni relativi ai numeri dal 10 al 20 che sembrano assegnare qualche particolarità a questi numeri speciali.
Ma i primi risultati di una qualche rilevanza matematica risalgono agli antichi Greci, e in particolare agli Elementi di Euclide, datati attorno al 300 a.C. In questo libro di trovano il teorema dell’infinità dei numeri primi e il lemma di Euclide. Sempre ai Greci si deve l’invenzione del crivello di Eratostene, un semplice algoritmo che serve a definire se un numero è primo oppure no.
Nel 1600 lo studio dei numeri primi conobbe nuovo vigore grazie alle teoria di Pierre de Fermat e del monaco francese Marin Mersenne. Il primo sviluppò il piccolo teorema di Fermat e il teorema sulla somma di due quadrati; il secondo studiò i numeri primi come esponenti di particolari formule, dando origine ai “primi di Mersenne”.
Nonostante questo, numerose formule che li riguardano non sono state ancora dimostrate: ad esempio l'ipotesi di Riemann, la congettura di Goldbach e la congettura dei primi gemelli, che ad oltre un secolo dalla loro formulazione, non sono state ancora dimostrate.
Il mistero dei numeri primi
Ma perché i numeri primi sono così affascinanti? Probabilmente perché tutti si rendono conto della loro particolarità, anche chi non è esperto di matematica. Non a caso il libro di Paolo Giordano “La solitudine dei numeri primi” è diventato un best seller, anche grazie al fascino del suo titolo.
In più, uno degli usi più importanti dei numeri primi è legato alla crittografia, cioè alla capacità di scrivere messaggi cifrati. Infatti, la difficoltà di fattorizzare grandi numeri ha portato allo sviluppo di un metodo efficace di crittografia a chiave pubblica. In questo sistema, chi deve ricevere un messaggio cifrato genera una chiave formata da tre numeri: uno è il prodotto di due numeri primi di grandi dimensioni, mentre gli altri due sono l'uno l'inverso dell'altro modulo. Uno tra questi ultimi due numeri deve essere tenuto segreto e dunque diventa la chiave privata, mentre l'altro deve essere reso noto andando a formare la chiave pubblica.
E se parliamo di numeri misteriosi e affascinanti, non si può non pensare alla famosa successione di Fibonacci, che splende dalla cupola della Mole Antonelliana di Torino e che è stata portata alla conoscenza del grande pubblico dal film “Il Codice da Vinci”. Nella successione di Fibonacci ogni numero (eccetto i primi due) è la somma dei precedenti due: quindi i primi numeri di Fibonacci sono 0, 1, 1, 2, 3, 5, 8, 13, 21 e così via. Ovviamente nella serie ci sono anche numeri primi: il più grande numero primo di Fibonacci (81.839) è stato segnalato nel 2001 da David Broadbent e Bouk de Water.





Mi mancava leggere sulle pagine di Elettronica Open Source articoli di matematica, che certamente deliziano la community ma soprattutto estendono l’invito alla lettura del blog anche a coloro che di tecnologia o di elettronica ne sanno poco e niente…alla fine alla base c’è sempre la matematica ed è la chiave di interpretazione di tutti i fenomeni fisici che ci circondano. Senza la matematica non avremmo sviluppato la conoscenza del mondo di cui siamo possessori oggi. Ma la matematica, nella sua misteriosa veste, non è solo strumento di interpretazione, ma anche motivo di grande fascino.
L’argomento numeri primi non è solo affascinante per i segreti che sono nascosti dietro, ma è anche la base di algoritmi crittografici altamente sicuri che oggi vengo adottati in tutti i contesti in cui c’è da attuare una transizione sicura di dati. Per mia pura curiosità, ho studiato l’algoritmo proposto nell’articolo (chiave pubblica + chiave privata) inserito nell’ambito della sicurezza dei dati inviati via rete internet. Devo dire che l’algoritmo, in se, non è così complesso da capire, ma occorrono basi matematiche di algebra modulare che sinceramente io non avevo mai studiato e che ho dovuto vedere per capire come avvenisse la cifratura del dato trasmesso e la relativa decifratura del dato ricevuto. Per chi volesse approfondire sull’algebra modulare, riporto la seguente pagine di Wikipedia: http://it.wikipedia.org/wiki/Aritmetica_modulare
mentre per un approfondimento sugli algoritmi di cifratura basati sull’utilizzo dei numeri primi, consiglio il seguente sito dove si possono trovare sia le implementazioni degli algoritmi che un riassunto sull’algebra modulare (da questo punto di vista sostituisce la pagina wiki precedente):
http://www.angelfire.com/yt3/ciphertext/algebra.htm
La matematica è fondamentale nella progettazione elettronica, dalla semplicità dei timer fino a modelli più complicati come la cinematica nella movimentazione di più bracci meccanici, passando per la rappresentazione matematica di un pwm nell’apertura cancelli.
Al tempo stesso la matematica offre anche aneddoti e curiosità molto divertenti, dei passatempo appunto.
I numeri primi, il loro fascino e la loro storia ne sono appunto un esempio.
Per completare l’articolo si potevano citare i numeri primi gemelli, dove la differenza tra i due numeri primi è 2 che ha inspirato Paolo Giordano a scrivere il romanzo “La solitudine dei numeri primi”, poiché tra di loro c’è sempre un altro numero in mezzo e quindi non saranno mai vicini, da cui è scaturito il film omonimo. Oltre a questi vi sono i numeri primi cugini la cui differenza è 4.
Potrei stare qua a scrivere sui numeri primi una giornata intera! i numeri primi sono veramente qualcosa di magico.
Università, esame di cui non ricordo il nome ma di cui mi ricordo benissimo il progetto: implementare su un microcontrollore motorola (ora l’attuale freescale) un algoritmo di crittografia che si basa sui numeri primi e più precisamente l’algoritmo RSA con chiave di crittografia a 64 bit (mi sembra). Ora non mi chiedete la teoria di questo algoritmo perchè, seppur molto affascinante oltre che interessante, non me la ricordo, ricordo solo che il suo punto di forza si basa proprio sul fatto che non è possibile sapere con una funzione ben precisa l’n-esimo numero primo; l’unico modo per saperlo è di far ” spremere le meningi ” ai calcolatori più sofisticati che con algoritmi super ottimizzati riescono a calcolartelo dopo svariato tempo. Insomma l’RSA è un algoritmo di crittografia che è difficile da ” crackare ” perchè è difficile trovare un numero primo sufficientemente grande.
Tralasciando le sorti del progetto (è durato una marea di tempo e alla fine lo abbiamo lasciato ad un altro gruppo di studenti…poveretti loro) da quel momento in poi mi sono interessato al mondo dei numeri primi, infatti, dovendo studiare questo algoritmo, inevitabilmente abbiamo dovuto studiare il mondo dei numeri primi e quindi tutte le loro formule e teoremi (fantastici). Dapprima ho iniziato a cercare documenti su internet e poi a guardare e riguardare ciò che ci era stato da supporto per il progetto. Un giorno passando per caso in una libreria, vidi un libro (anzi il libro direi io) “L’enigma dei numeri primi” e la mia attenzione si fermo subito su di lui. Ero di fretta e quindi non lo presi ma chi era con me si accorse e me lo fece per regalo 🙂
Bè non c’è che dire, proprio un bel regalo per uno che come me era “preso” dai numeri primi 🙂 in questo libro si parla di Riemann e della formula da lui scoperta, basata sulla funzione “Z” e che riproduce “l’andamento” dei numeri primi (dato un numero “n” restituisce l’n-esimo numero primo). La formula sembra funzionare se confrontata con gli attuali numeri primi già calcolati ma peccato però che la sua dimostrazione è andata persa a causa di una “badante” poco ordinata. Da quel momento fino ad oggi, molti matematici si sono arrovellati nella dimostrazione di questa formula o nella formulazione di altre teorie ma nessuno è mai riuscito nell’obbiettivo. Questa “avventura” ha portato però alla scoperta di altre formule e teoremi che sembrano tutti “convergere” verso quella formula lasciata da Riemann più di un secolo fa e ad oggi tramutata in una sfida da svariati migliaia di euro…insomma un vero e proprio giallo della matematica!