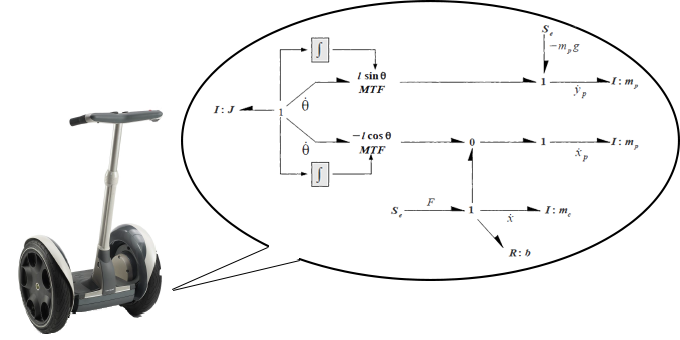
Lo scopo dell’articolo è quello di analizzare il funzionamento di un sistema fisico realizzato connettendo ad un carrello un’asta rigida, modellando il sistema mediante differenti approcci (Newtoniano, Lagrangiano e Bond Graph), mettendo in risalto vantaggi e svantaggi di ognuno di essi. L'asta è collegata attraverso un perno incernierato sul carrello ed è libera di ruotare intorno ad esso. Tale sistema meccanico, che prende il nome di pendolo inverso, è un classico problema nella teoria del controllo. In genere è largamente utilizzato per valutare le prestazioni di algoritmi di varia natura (Controllori PID, Reti Neurali, Fuzzy Logic, Algoritmi Genetici, etc.). Esempio lampante è il Segway, analizzato al termine della trattazione.
1. Modellistica fisica
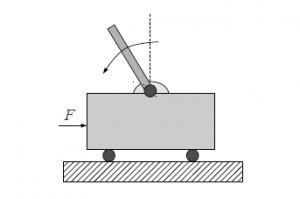
Il pendolo inverso (Figura 1) è un sistema fisico di tipo meccanico soggetto ad una forza esterna F utilizzata per il controllo.
Figura 1: Sistema fisico analizzato.
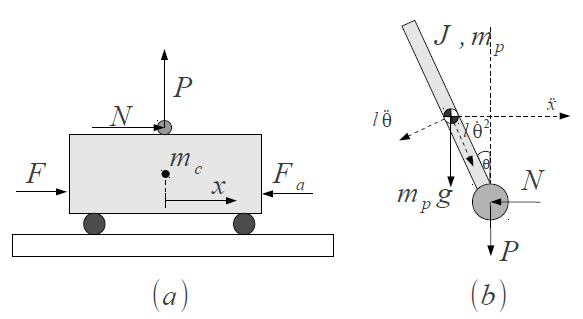
La modellistica è notevolmente semplificata dalla decomposizione logica dell’oggetto in due sottosistemi (Figura 2) separati:
- Carrello;
- Asta rigida.
Il carrello è considerato un punto materiale di massa mc su cui agiscono oltre alla forza esterna F anche la forza d’attrito con il suolo e le forze di reazione del pendolo N e P. In virtù del principio di azione e reazione tali forze assumono un ruolo duale nello schema del pendolo che viene considerato un corpo rigido di massa mp e momento di inerzia J rispetto al centro di massa. Le forze interne N e P si considerano applicate al punto di rotazione mentre la forza peso mp·g è applicata al centro di massa.
Figura 2: Decomposizione del sistema fisico; (a) carrello; (b) asta.
1.1 Sistema di riferimento
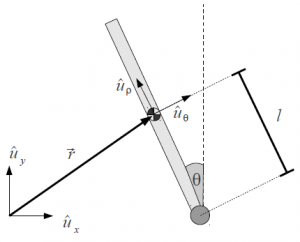
Prima di descrivere la dinamica dei due componenti è necessario stabilire un sistema di riferimento appropriato per ognuno di essi. Per il carrello è possibile considerare un sistema di assi (O, ux, uy) tale che la posizione x(t) del carrellino all’instante iniziale t0=0 sia nulla. Nella seconda struttura la scelta più naturale è di stabilire un sistema di assi in coordinate polari (O,uρ,uθ) come descritto in Figura 3.
Figura 3: Sistemi di riferimento.
Tale scelta tuttavia conduce ad [...]
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2881 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.
Ti potrebbe interessare anche:
OpenMV Cam: l’Arduino della visione artificiale
Firmware 2.0 #19 – Open Source IoT/Embedded Systems Design
Memorizziamo i dati in maniera sicura con il confidential computing
Streaming di temperatura e umidità con l’ecosistema Big Data – Parte 2
Sensori industriali: caratterizzazione, principi di funzionamento e applicazioni
Credo che sia sfuggito un cos nella derivata dell’equazione (1.2)…altrimenti non puoi scrivere la (1.4).
Si, hai pienamente ragione. Sarà stato un refuso. Grazie della correzione.
Complimenti
Grazie! Spero di essere stato quanto il più chiaro possibile.
La progettazione del Segway è stata fatta utilizzando gli strumenti di programmazione che Matlab mette a disposizione, Simulink compreso. Sul sito della Mathworks digitando “Inverted pendulum” escono molti script per simulare le equazioni sopra.