L'articolo affronta lo sviluppo di un’applicazione "pick and place" per un robot manipolatore in ambiente MATLAB/Simulink, uno dei problemi classici nella smart manufacturing. L'articolo mostra come rilevare e riconoscere un oggetto attraverso una fotocamera RGB-D, eseguire calcoli di cinematica diretta ed inversa, e generare la traiettoria di un braccio manipolatore in presenza di ostacoli lungo il percorso. L'intero scenario è modellato e simulato in MATLAB/Simulink ed attraverso un ambiente di simulazione esterno 3D, Gazebo. L'Optimization Toolbox della MathWorks è impiegato per sintetizzare la traiettoria ottima minimizzando un fissato funzionale di costo, mentre il rilevamento e la classificazione di oggetti è ottenuta impiegando tecniche di machine learning e computer vision, accessibili attraverso i toolbox disponibili in MATLAB. La chiave di lettura data all'articolo è educational, dunque l'intero approccio è descritto ad alto livello lasciando poi al lettore il compito di approfondire ed entrare nel dettaglio tecnico implementativo degli aspetti presentati.
Introduzione
MathWorks - nota azienda multinazionale privata specializzata nella produzione di software per calcoli matematici - collabora da anni con il mondo accademico ed industriale per risolvere problemi complessi in ambito robotico, ma non solo. L'articolo si pone l'intento di spiegare come realizzare un robot pick and place in MATLAB/Simulink passando attraverso un esempio (Figura 1).
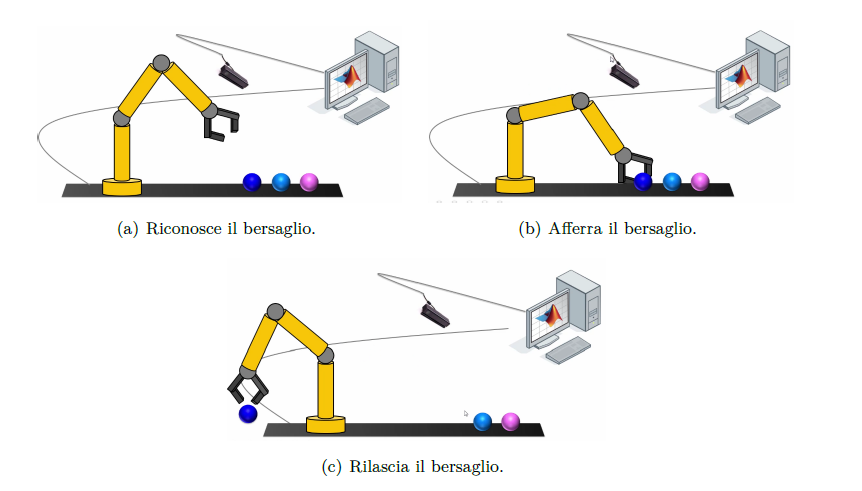
Figura 1: Attività di esempio di un robot manipolatore
Si immagini di possedere un robot ed un sensore di tipo RGB-D (Red Green Blue and Depth), ad esempio un Microsoft Kinect. L'obiettivo è individuare oggetti specifici dall'immagine catturata dal sensore, pianificare una traiettoria da seguire minimizzando un funzionale di costo, per poi afferrare l'oggetto bersaglio spostandolo in una posizione differente da quella iniziale, come illustrato in Figura 1. Il classico esempio che riguarda applicazioni nel campo della smart manufacturing, che coinvolge aspetti quali:
- la pianificazione della traiettoria;
- l'individuazione e la stima della posizione degli oggetti;
- l'integrazione di tutte le componenti hardware e software.
Per poter affrontare un problema di questo tipo è necessario avere una minima conoscenza:
- della teoria della robotica e dell'ottimizzazione (matrici di rotazione, Newton-Eulero, Lagrange, etc.);
- del trattamento delle immagini (computer vision) e machine learning;
- di logica ad eventi discreti (automi a stati finiti, reti di Petri);
- dell'utilizzo di simulatori esterni di dinamica 3D (Gazebo, V-REP, AirSim, MORSE, etc.);
- di generazione automatica di codice sorgente (model based design).
Tecnologie molto diverse tra loro ma totalmente integrate all'interno di MATLAB/Simulink, che fornisce strumenti avanzati per lo sviluppo di applicazioni avanzate in tutti i settori dell'ingegneria.
Da dove si parte?
La domanda che sorge spontanea è: da dove si parte per descrivere il sistema? Si inizia da una descrizione dell'applicazione ad un livello di astrazione elevato, come quello in Figura 2.
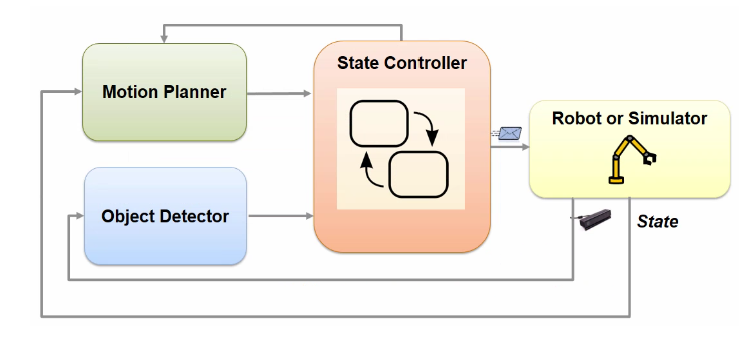
Figura 2. Schema ad alto livello del problema
Nello schema, un riconoscitore di oggetti (object detector) processa le informazioni provenienti dal sensore RGB-D, oltre alle immagini a colori, fornisce anche una misura di profondità, e ritorna di un identificativo della posizione presunta dell'oggetto bersaglio. Il pianificatore di traiettoria (motion planner) determina un percorso a partire dallo stato iniziale e finale del robot, mentre il sistema di supervisione (state controller) gestisce le interazioni tra i diversi componenti e restituisce i profili di moto angolare da fornire al simulatore o, nel caso reale, agli azionamenti del robot; l'attuazione nei robot manipolatori è fornita fornendo coppia ai motori posizionati nei giunti.
Generatore di traiettoria
Il generatore di traiettoria (motion planner) utilizza le informazioni su posizione iniziale e finale del robot nello spazio cartesiano, fornite dal processo di riconoscimento del bersaglio (Figura 3), per calcolare i profili di moto delle varie sezioni del braccio robotico generando così la traiettoria richiesta.
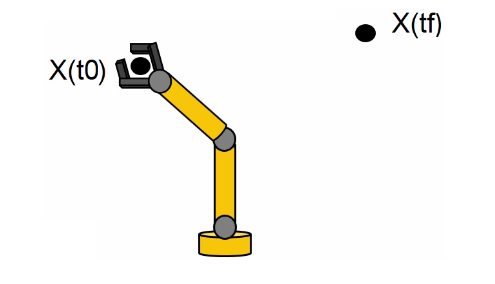
Figura 3: Rappresentazione dello stato iniziale e finale del robot
Una prima traiettoria (Figura 4), la più semplice da ottenere (una banale retta), potrebbe essere sottoposta a vincoli come la presenza di ostacoli lungo il percorso. In questo caso, le spline cubic (Figura 5) costituiscono una, ma non l'unica, soluzione al problema. Consentono di generare una traiettoria capace di aggirare l'ostacolo e ben si prestano ad essere impiegate in problemi di ottimizzazione. Per tutti coloro che non fossero avvezzi a questi linguaggi, una spline è una funzione matematica costituita da un insieme di polinomi raccordati tra loro, il cui scopo è interpolare in un intervallo un insieme di punti (detti nodi della spline), in modo tale che la funzione sia continua almeno fino ad un dato ordine di derivate in ogni punto dell'intervallo.
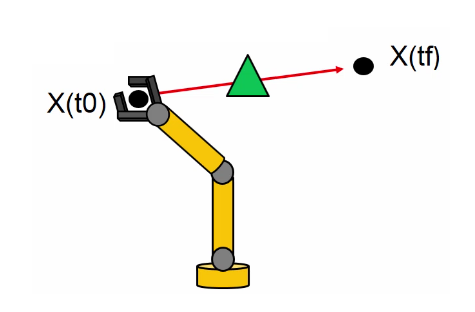
Figura 4: Esempio di traiettoria (in rosso) sottoposta a vincoli (in verde)
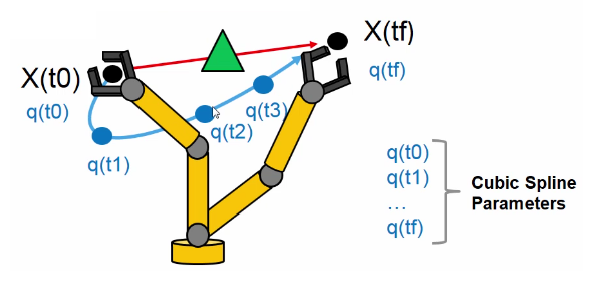
Figura 5: Traiettoria generata utilizzando le spline cubic
In termini di workflow (Figura 6), si parte da una rappresentazione del robot in MATLAB per risolvere problemi di cinematica inversa (a partire dalle posizioni nello spazio, si calcolano gli angoli dei giunti q(t)) partendo dalla rispettiva posizione iniziale e finale, tenendo in conto i vincoli del caso. Successivamente, utilizzando le librerie di modellazione fisica, si costruisce il robot in Simulink formulando le funzioni di costo necessarie a stimare la coppia richiesta al manipolatore. Infine, servendosi degli strumenti di ottimizzazione, si calcolano i parametri delle spline cubic che minimizzano il funzionale di costo, sulla base dei vincoli definiti al passo precedente, al fine di ottenere una traiettoria estremamente regolare. Il tutto può essere strutturato in ambiente MATLAB/Simulink servendosi del Robotics System Toolbox.
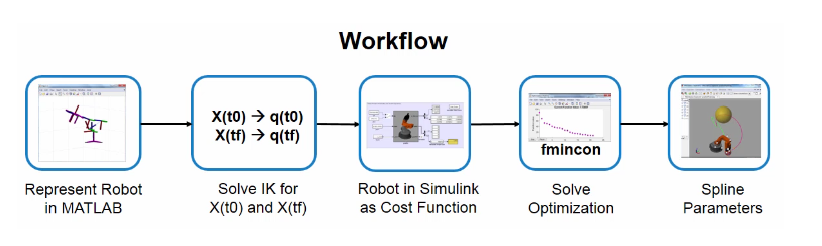
Figura 6: Robot workflow
Il toolbox consente di creare un albero di trasmissione del moto ed uno rigido per il calcolo della cinematica diretta (processo contrario, a quella inversa: da q(t) alle posizioni nello spazio) ed inversa. La seconda risulta particolarmente utile quando si lavora con il generatore di traiettoria. Inoltre, servendosi del supporto grafico, è possibile osservare la struttura del robot effettuando calcoli di cinematica diretta (Figura 7).
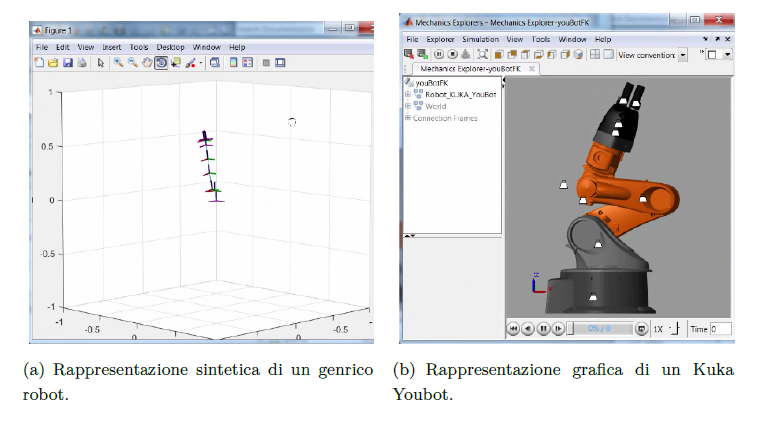
Figura 7: Rappresentazione di un robot nel Robotics System Toolbox
Simulink
Ponendo in secondo piano, almeno per il momento, l'ambiente MATLAB, si può utilizzare quello Simulink (Figura 8) per modellare il comportamento del robot. Nella fattispecie, si è fatto appello alle librerie di modellazione fisica Simscape Multibody e SimMechanics (Figura 9).
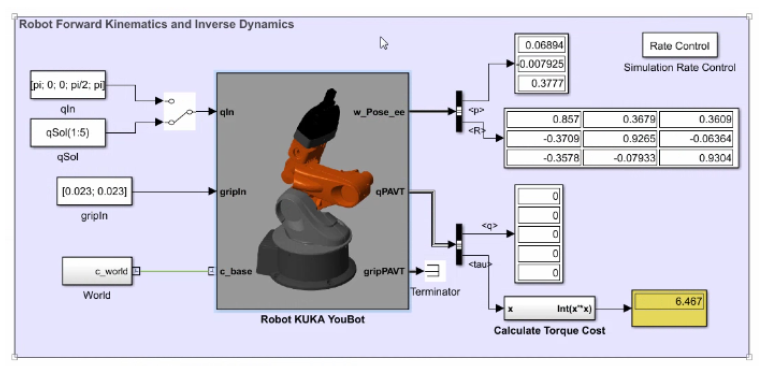
Figura 8: Simulazione Kuka Youbot in ambiente Simulink
L'utilizzo dello schema Simulink consente di visualizzare il comportamento del robot con un elevato grado di dettaglio grafico facilitandone la configurazione all'interno del modello. Per giunta, è possibile risolvere il problema di cinematica diretta ed inversa calcolando le coppie coinvolte oltre al funzionale di costo, ottimizzando così i parametri del sistema. La funzione di costo è ottenuta integrando il quadrato della coppia che esprime, nell'esempio preso in considerazione, il costo da minimizzare.
Rilevante, nella libreria di modellazione fisica di Simulink, è la facilità con cui è possibile sostituire la coppia (il costo da minimizzare), supponendo di inserire un azionamento elettrico, con la potenza elettrica modificando così il problema di partenza. Il ventaglio di possibilità che si aprono con l'uso di Simulink si espande notevolmente giustificando l'approccio al problema anche dal punto di vista della simulazione. Risultando, dunque, da subito evidenti le potenzialità dello schema.
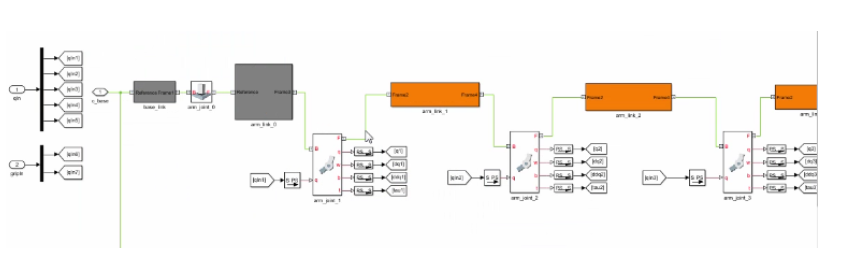
Figura 9: Rappresentazione di un robot utilizzando Simscape Multibody e SimMechanics
Per affrontare il problema di ottimizzazione dei parametri si è preso in considerazione lo schema, non troppo dissimile dal precedente, in Figura 10. La sostanziale differenza tra i due è da ricercare nella generazione della traiettoria dei giunti: nel primo caso formulata attraverso l'utilizzo di costanti, nel secondo realizzata servendosi delle spline cubic costruite utilizzando delle lookup table (Figura 11) che ne inglobano i coefficienti interpolati per generare i percorsi. Nello schema in Figura 10, inoltre, viene verificato il raggiungimento dei limiti di soglia degli angoli e calcolata la distanza fra una determinata parte del braccio ed un ostacolo attraverso un modello di collisione.
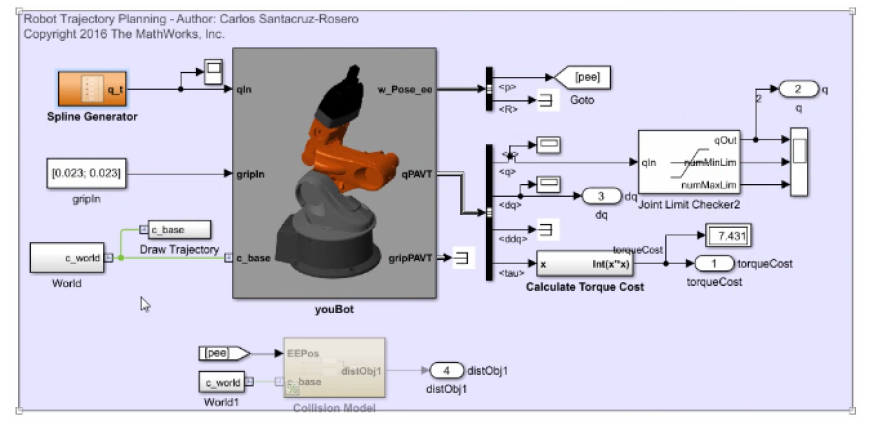
Figura 10: Schema Simulink per la risoluzione del problema di ottimizzazione
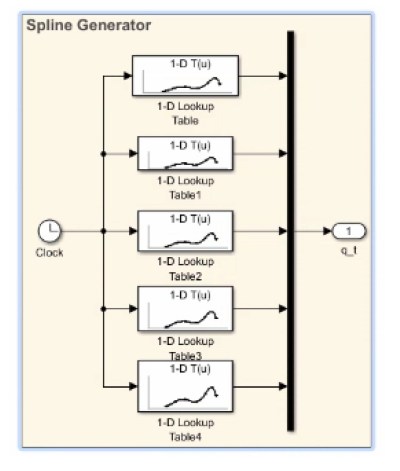
Figura 11: Costruzione delle spline cubic utilizzando le lookup table
Utilizzando il modello appena descritto è possibile osservare graficamente (Figura 12(a)) il braccio mentre percorre la traiettoria più semplice composta da soli punti discreti equivalenti ai parametri da ottimizzare. La traiettoria è ottenuta collegando lo stato iniziale e finale del robot.
Servendosi della funzione fmincon dell'Optimization Toolbox, si risolve il problema di ottimo corrispondente, minimizzando il funzionale di costo e ricavando così la traiettoria ottima in Figura 12(b). In Figura 12(c) è possibile osservarle entrambe, rendendo ancora più evidente le differenze tra le due.
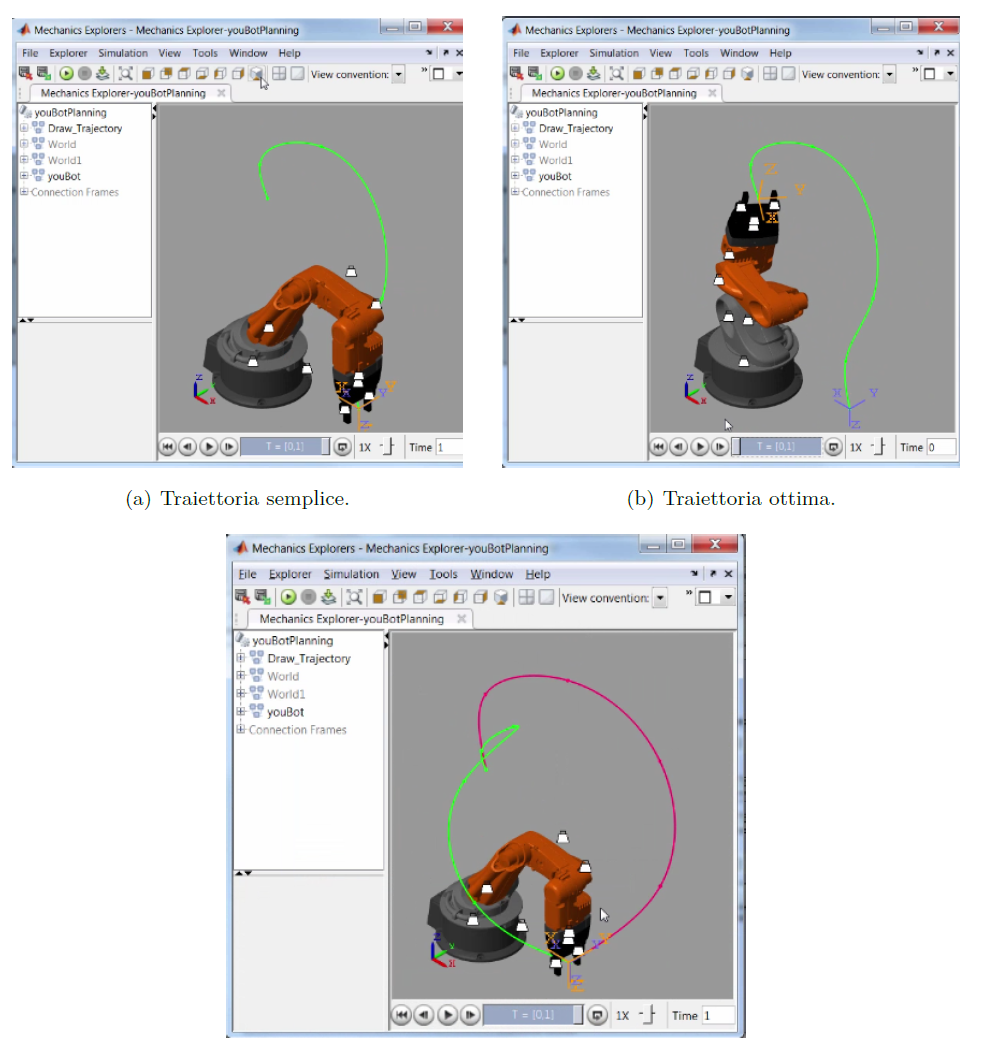
Figura 12: Rappresentazione grafica del robot nel mentre percorrere la traiettoria
Osservando il risultato del problema di ottimizzazione (Figura 13) sono evidenti i risparmi economici immediatamente fruibili dopo sole poche iterazioni, soprattutto se il robot ripete più volte la stessa operazione. Difatti, dopo 23 iterazioni, la funzione di costo si riduce sensibilmente nonostante i vincoli continuino ad essere rispettati. I suddetti, oltre a tenere in conto posizione finale ed iniziale del robot, considerano anche i precisi valori angolari lungo la traiettoria.
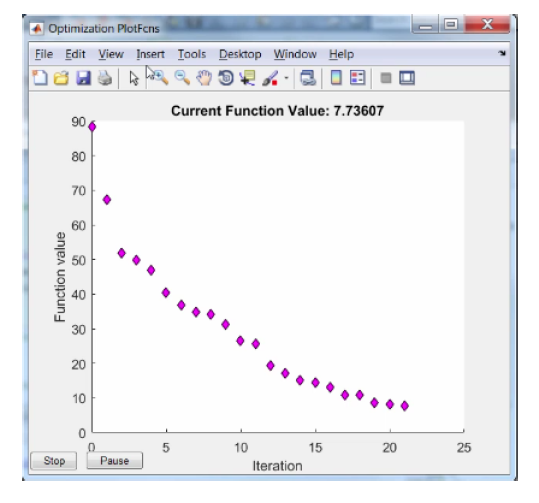
Figura 13: Risultato problema di ottimizzazione
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3059 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.