Programmare con la Macchina di Turing – simuliamo Enigma

Dopo il mio primo articolo sulla programmazione della Macchina di Turing descriverò brevemente il funzionamento della macchina di Scherbius ovvero la famigerata Enigma. Enigma è un vero e proprio capolavoro di logica matematica e nell'arco di tempo in cui è stata utilizzata, i messaggi criptati con tale strumento hanno messo in crisi i migliori scienziati dell’epoca.
Dopo aver visto di cosa si tratta proveremo a realizzarne una niente di meno che con la Macchina di Turing! Ebbene sì, simuleremo Enigma codificando e decodificando i messaggi sfruttando la logica del suo meccanismo ma con algoritmi realizzati col linguaggio della Macchina di Turing e funzionanti su quest’ultima.

Crittografia con la Macchina di Turing

Nel mio articolo sulla programmazione con la Macchina di Turing ho spiegato quali sono i costrutti di tale linguaggio. Abbiamo visto che programmare con tale paradigma è tutt’altro che semplice.
Nel campo della codifica-decodifica delle informazioni però forse la Macchina di Turing non risulta così ostica come per altre tipologie di algoritmi.
In fin dei conti si tratta “solo” di sostituire un simbolo con un altro secondo una certa regola.
Si potrebbe pensare di associare ad ogni lettera di un qualunque alfabeto una qualsivoglia altra lettera dell’alfabeto stesso. Prendiamo le lettere

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

e creiamo una funzione bigettiva che associ ad ognuna di esse un’altra lettera basandoci sulla sua posizione all'interno dell’alfabeto. Ad esempio potremmo basarci sulla seguente chiave

W G Z D A F Q H L J K O M N I U B R S T P V E X Y C

In questo modo alla lettera A (prima posizione nel primo alfabeto) corrisponderebbe la W (prima posizione nel secondo alfabeto), alla B (seconda posizione nel primo alfabeto) la G (seconda posizione del secondo alfabeto) ecc.
Ovviamente questo modo di crittografare, al giorno d’oggi è troppo banale e i messaggi sarebbero decrittati all'istante ma a noi interessa per ora fare solo un po’ di riscaldamento con la crittografia con la Macchina di Turing prima di passare alla ben più sofisticata Enigma.
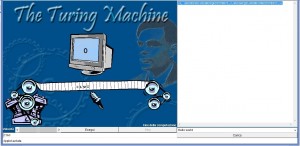
Tornando all'algoritmo precedente la codifica dei messaggi con la Macchina di Turing sarebbe veramente molto banale e potrebbe consistere addirittura in una sola istruzione (Figura 1).

(0, ABCDEFGHIJKLMNOPQRSTUVWXYZ,0,WGZDAFQHLJKOMNIUBRSTPVEXYC,>)

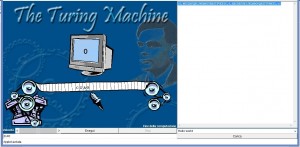
Figura 1: Simulatore Macchina di Turing

Altrettanto semplice sarebbe la decodifica (Figura 2):

(0,WGZDAFQHLJKOMNIUBRSTPVEXYC,0,ABCDEFGHIJKLMNOPQRSTUVWXYZ,>)

Figura 2: Simulatore Macchina di Turing

Bene, la logica di base è tutta qui. Ora vediamo come trasportare il tutto confrontandoci con il funzionamento ben più complesso di Enigma.

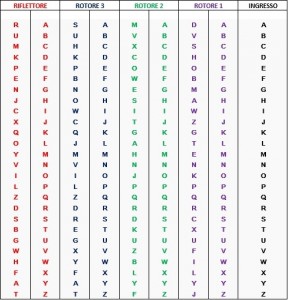
Funzionamento di Enigma

Figura 3: Schema di una codifica Enigma

Di trattazioni, libri, articoli, guide, immagini sulla macchina Enigma, su Turing, sulla crittografia ne esistono parecchi quindi vi risparmio la sua storia arcinota. Il mio intento è quello di descriverne invece il meccanismo logico e ancora una volta approfittare dell'argomento per divertirci con la logica [...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2240 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.