
Questo studio nasce seguendo le direttrici dettate da un approccio matematico "trasversale" ritenendo utile osservare ciò che accade nell'insieme N da una prospettiva geometrica, rifacendosi, in particolare, alla visione che David Hilbert aveva della matematica pura, i cui caratteri precipui sono: astrazione, generalizzazione e unificazione. E’ noto che Hilbert propose di studiare il comportamento dei numeri primi su campi arbitrari ed è per questi motivi che, qui, sulla scia della proposta del celebre matematico, si è cercato di studiare il comportamento dei numeri naturali maggiori di 1 in un campo P*k ovvero un campo k-dimensionale dove P* rappresenta l’insieme dei numeri primi positivi.
Introduzione
Il modo di procedere dell’indagine matematica proprio di David Hilbert (Königsberg 1862 – Gottinga 1943) fece ricorso a metodi diretti, sovente non costruttivi, e fu per questo che egli riuscì a superare frequentemente ostacoli concettuali che bloccarono altri suoi illustri colleghi. Nel pensiero hilbertiano le costruzioni dei singoli enti si rendono inessenziali ed in questo consiste il valore delle dimostrazioni di natura puramente esistenziale; in aggiunta il celebre matematico sostenne che edifici matematici estremamente diversi possono venire convogliati e ricondotti ad un’unica teoria fondamentale.
Geometria e numeri Naturali
Questo lavoro prende il via dal teorema fondamentale dell’aritmetica, teorema a cui lavorò assiduamente il matematico Johann Carl Friedrich Gauss (Braunschweig 1777 – Gottinga 1855) e che giunse a dimostrarlo esplicitamente, per la prima volta, nelle Disquisitiones Arithmeticae. Il teorema asserisce che: "ogni numero naturale maggiore di 1 o è un numero primo o si può esprimere come prodotto di numeri primi. Tale rappresentazione è unica, se si prescinde dall'ordine in cui compaiono i fattori".
Infatti, per numeri piccoli, è facile verificare la correttezza del teorema: 10 = 2*5; 12 = 2*2*3; 20 = 2*2*5 e così via. Il processo di individuazione dei fattori primi prende il nome di scomposizione in fattori primi. Nell’ esporre i concetti matematici useremo notazioni proprie sia del linguaggio logico-insiemistico sia della geometria ovvero:
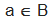
(si legge a appartiene a B);
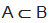
(si legge A sottoinsieme di B);

(si legge l’unione di A e B);
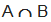
(si legge l’intersezione di A e B);

(si legge l’insieme differenza A meno B);
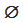
(si legge l’insieme vuoto);
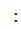
(si legge tale che ed è l’equivalente del simbolo |);

quantificatore esistenziale (si legge esiste un/una);
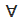
quantificatore universale (si legge per ogni)

connettivo logico (si legge et o e)

(prodotto vettoriale tra i vettori wpi)
en
(vettori della base canonica di P*k)
Cominciamo col considerare la funzione di scomposizione in fattori primi come una funzione così definita:
dove
La freccia indica che la funzione 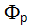 è una funzione a valori in P*k, definita nell’insieme dei numeri naturali maggiori di 1, mediante cui, grazie al sopracitato teorema fondamentale dell'aritmetica, ad ogni numero naturale n maggiore di 1 corrisponde almeno un vettore
è una funzione a valori in P*k, definita nell’insieme dei numeri naturali maggiori di 1, mediante cui, grazie al sopracitato teorema fondamentale dell'aritmetica, ad ogni numero naturale n maggiore di 1 corrisponde almeno un vettore
dove
con pi primo
rappresenta l’insieme dei numeri primi positivi.
Esempio:
Come si può notare, al numero naturale 10, corrisponde un elemento immagine:
di componenti (2, 5). In base a questo approccio geometrico possiamo esporre una serie di enunciati:
1) ad ogni numero naturale x maggiore di 1 corrisponde almeno un elemento immagine nel campo P*k:
2) INIETTIVITA’: per il teorema fondamentale dell’aritmetica si ha che se
3) la dimensione del campo P*k è funzione del numero x considerato (ovvero dim P*k(x)) in quanto
5) per i numeri naturali maggiori di 1 valgono le seguenti proprietà:
- esistono numeri (oltre ai numeri primi) la cui immagine ha come modulo un numero primo, per esempio:
- esistono numeri la cui immagine ha il quadrato del modulo che corrisponde ad un numero primo, per esempio (altri numeri sono 40 e 45):
6) le seguenti affermazioni sono equivalenti:
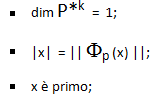
7) rispetto a ciò che avviene in N (dove |x+1| >|x|), in P*k la disuguaglianza
non è più valida;
8) rispetto a ciò che avviene in N, dove la scomposizione in fattori primi è unica, qui, nel caso di numeri non primi, e nel caso in cui la scomposizione non origini componenti tutte uguali, una scomposizione individua n-elementi immagine appartenenti a P*k con n >=2 in quanto l’ordine con cui consideriamo le componenti origina elementi immagine diversi. Quindi, nei casi suddetti, ad ogni scomposizione risulta possibile associare una matrice primale:
il cui rango
come conseguenza della definizione propria di numeri primi.
9) esistono numeri co-dimensionali consecutivi (come 9 e 10) ;
10) esistono numeri co-dimensionali gemelli (come 4 e 6);
11) come conseguenza del punto 3) si ha che il teorema fondamentale dell'aritmetica non è applicabile in
dove
ovvero non è sempre possibile scrivere un
come prodotto componente per componente di n elementi wpi appartenenti a P*k.
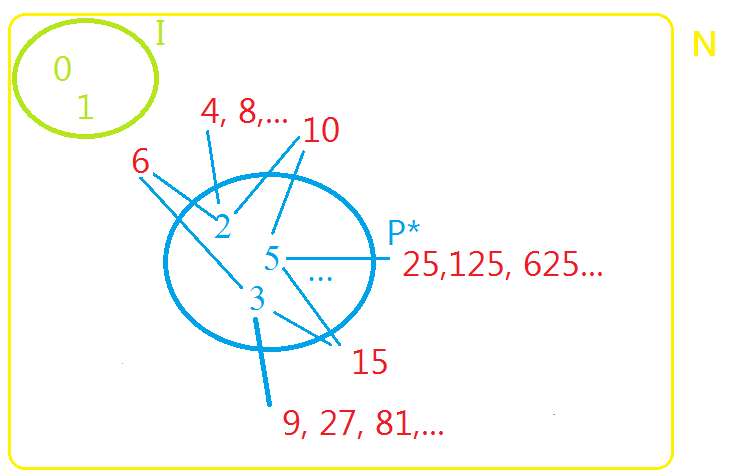
P*k risulta essere il sottoinsieme generatore di
solo nel caso k = 1, come mostrato dalla seguente figura 1, dove
Conseguenza: definizione assiomatica di N
Possiamo quindi definire assiomaticamente l'insieme dei numeri naturali nel modo seguente:
1) esiste l’insieme N ed esiste una funzione
chiamata divisione;
2) esiste un sottoinsieme
in cui l’elemento maggiore iM (chiamato divisore universale) è l’unico elemento di N (UNICITÀ IN N DEL DIVISORE UNIVERSALE) tale per cui la divisione di ogni elemento appartenente ad N per quest’ ultimo, è ancora un elemento appartenente ad N.
L’elemento minore im di I (chiamato dividendo universale) è l’unico elemento di N (UNICITÀ IN N DEL DIVIDENDO UNIVERSALE) tale per cui la divisione di questo per ogni elemento appartenente ad N\{im} è ancora un elemento appartenente ad N.
3) esiste un sottoinsieme
tale per cui ogni suo elemento k ha almeno un elemento appartenente ad
tale che il risultato della divisione di k per questo è ancora un elemento appartenente ad
4) gli elementi che appartengono a
sono chiamati elementi primi e formano il sottoinsieme generatore P*.
Esprimendo il tutto in termini logico-matematici otteniamo:
Come si può notare siamo giunti (mediante un approccio puramente insiemistico) a descrivere l’insieme dei numeri naturali N secondo un sistema assiomatico che differisce da quello proposto dal matematico Giuseppe Peano (Spinetta di Cuneo 1858 - Torino 1932) per tre aspetti:
- Per Peano i concetti primitivi sono tre: lo zero, il numero e la funzione di successione di un numero che individua tutti gli elementi di N. Qui i concetti primitivi sono due: l’insieme N e la funzione divisione che individua tutti gli elementi dell’insieme N.
- Peano ha un approccio bottom-up infatti parte dall’elemento per giungere all’insieme. Qui l’approccio è top-down ovvero si parte dall’insieme per giungere agli elementi.
- Peano non introduce differenze tra gli elementi propri di N mentre qui gli elementi di N vengono distinti sulla base degli assiomi stessi.
Inoltre, questo sistema assiomatico consente la normalizzazione in I di N:
Secondo questa definizione assiomatica dell’insieme N valgono le seguenti affermazioni:
Infine, l’elemento minore w*m di W è un elemento primo anomalo in quanto, a differenza degli altri elementi k di W (caratterizzati dal fatto che nessuno degli elementi di N compresi nell’intervallo (iM, k) li divide interamente), non ha nessun elemento di N compreso nell’intervallo (iM, w*m).
Conseguenza: congettura di Goldbach
Alla luce di quanto fin qui enunciato, abbiamo delle ripercussioni anche su uno dei più vecchi problemi irrisolti nella teoria dei numeri: la congettura di Goldbach. Nella versione di Eulero (versione nella quale è formulata attualmente, talvolta chiamata anche congettura forte di Goldbach) essa afferma che ogni numero pari maggiore di 2 può essere scritto come somma di due numeri primi (anche uguali). Da quanto fin qui esposto, questa congettura potrebbe risultare o un caso particolare o il presupposto di una congettura più ampia la quale asserisce che:
Ogni elemento v avente tutte componenti pari appartenente ad un insieme 2N*k può essere scritto come somma di almeno 2 elementi wpi (eventualmente uguali) appartenenti a P*k aventi come componenti solo numeri primi
dove
Esempio:
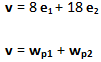
dove: wp1 = 3 e1 + 7 e2 , wp2 = 5 e1 + 11 e2; wp1 = 5 e1 + 7 e2 , wp2 = 3 e1 + 11 e2 ; wp1 = 5 e1 + 5 e2 , wp2 = 3 e1 + 13 e2; wp1 = 5 e1 + 13 e2 , wp2 = 3 e1 + 5 e2.
La stessa congettura di Goldbach può quindi essere vista come il risultato di una funzione  così definita:
così definita:
dove
Tale funzione, quindi, individua almeno due elementi nel codominio P*k. Ragionando a più dimensioni osserviamo che accadono fenomeni diversi da ciò che avviene in una dimensione. Infatti, per definizione, se moltiplichiamo due numeri primi tra di loro non otteniamo mai un terzo numero primo, invece, in più dimensioni, questo può avvenire sia per il prodotto scalare sia per il prodotto vettoriale. Prendiamo ad esempio l’elemento wp1 = 2 e1 + 3 e2 e l’elemento wp2 = 5 e1 + 7 e2, vediamo che il prodotto scalare wp1 * wp2 corrisponde al numero primo 31. Come si può notare wp1*wp2 appartiene a P*. Per quanto riguarda il prodotto vettoriale prendiamo l’elemento
wp1 = 2 e1 + 3 e2 + 5 e3 e l’elemento wp2 = 3 e1 + 2 e2 + 5e3.
Vediamo che il prodotto vettoriale
corrisponde all’elemento
Come si può notare


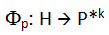
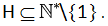
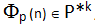
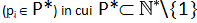
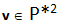
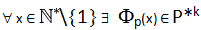
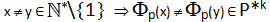
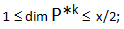
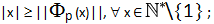

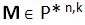
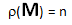
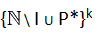
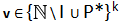
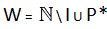

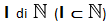


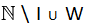
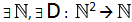
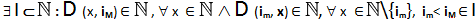
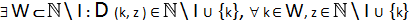
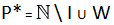
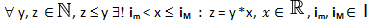
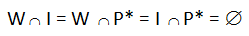

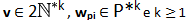
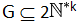
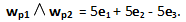
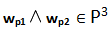





La congettura di Goldbach ha attirato molti matematici teorici, e non solo, proprio per cercare soluzioni che dimostrassero la teoria dei numeri primi. Lo studio condotto da Daniele in questo articolo ha voluto mettere in luce, decisamente bene, l’approccio geometrico che si differenzia dagli altri metodi. Ricordiamo che la congettura di Goldbach risale al 1700, precisamente 1742! Ora ci vengono in aiuto i calcolatori che possono implementare le varie espressioni per dare dei risultati immediati ed efficaci. Per esempio questo metodo potrebbe essere implementato con Matlab per dare graficamente l’idea dell’approccio.