Come dagli impegni presi, anche se con ingiustificabile ritardo, eccomi ad illustrare nei dettagli l'esempio numerico che mostra come la minimizzazione della figura di rumore non implica la massimizzazione del rapporto segnale rumore in uscita.
La figura iniziale, riportata qui di seguito,
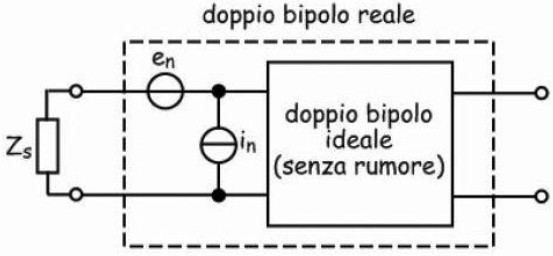
è lo schema di principio di un sistema sensore-amplificatore. Le caratteristiche di rumore dell'amplificatore si suppongono note e fisse. Esse vengono schematizzate con due generatori in ingresso proprio come accade nella più diffusa letteratura scientifica.
Sia A l’amplificazione del doppio bipolo e Zi la sua impedenza d’ingresso (non indicata). Siano inoltre:
Se la densità spettrale del generatore di rumore in tensione, supposta nota e pari a 10^-18 V^2/Hz
Si la densità spettrale del generatore di rumore in corrente, anch’essa nota e pari a 10^-24 A^2/Hz
St la densità spettrale del rumore generato dalla impedenza di sorgente e pari a 4KTRs
Su la densità spettrale del segnale utile.
Da questi dati, applicando le regole di dualità esistenti tra il calcolo simbolico e analisi spettrale è possibile scrivere l’SNR in uscita.
La formula (1)
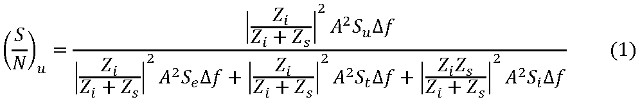
indica proprio l'SNR, ossia il rapporto tra il valor quadratico medio del segnale utile e il valor quadratico medio del rumore totale in uscita. Sul segnale utile non sono state fatte ipotesi particolari, si è supposto solo che sia descrivibile da un processo aleatorio di tipo stazionario.
Dove Δf indica la banda di lavoro ed inoltre, ça va sans dire, l’SNR in questo caso è da intendersi come rapporto tra il valor quadratico medio del segnale utile e il valor quadratico medio del rumore. Semplificando si ottiene:
Semplificando si ottiene la (2).
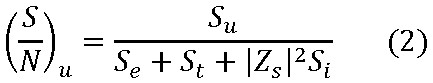
Nella (3)
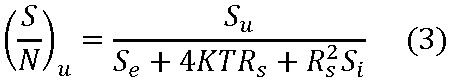
si ipotizza l'impedenza puramente resistiva e per la resistenza di sorgente il valore che minimizza la cifra di rumore (come indicato in letteratura) e si calcola il relativo SNR ottenendo la (4).
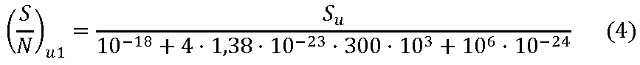
Analogamente nella (5),
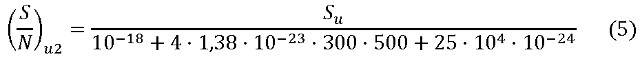
si suppone per essa un valore diverso (valore di comodo ai fini della dimostrazione) e si calcola il SNR. Facendo il rapporto dei due SNR, si ottiene il paradosso.
Si potrebbero fare altri esempi di tipo diverso che porterebbero alla stessa conclusione. Ad esempio, si potrebbe supporre un sistema sorgente-BJT dove l'unico parametro libero è la corrente di collettore. Si potrebbe dimostrare che scegliendo la corrente di polarizzazione che minimizza la figura di rumore, l'SNR non è massimizzato!
Nota: ho utilizzato le densità spettrali, ma identici risultati si ottengono con le medie temporali dei segnali in gioco elevati al quadrato.






Standing ovation e massima solidarietà per Lei, professore!
Lei ha perfettamente ragione.
Tuttavia, sarebbe anche giusto dire che non è che il 60% di voi docenti faccia di tutto per renderla meno ostica 🙂
Diciamo che io mi baso su quelo che so, sulla mia esperienza di studente (e le garantisco che ne ho passate di tutti i colori!!!) e su quello che ho fatto una volta averla studiata e cioè fare ripetizioni ad altri ragazzi dalle superiori fino all’università.
La matematica è un linguaggio, uno strumento, un mezzo e certamente non un fine.
Se i docenti si soffermassero per una lezione di due ore intere su questo e su tutto ciò a cui serve piuttosto che sciorinare esercizi a tutto spiano ininterrottamente FORSE la matematica farebbe appassionare più persone.
E lo dico e lo rivendico con orgoglio perchè questo modo di vedere le cose sono stato costretto a maturarmelo da me 🙂