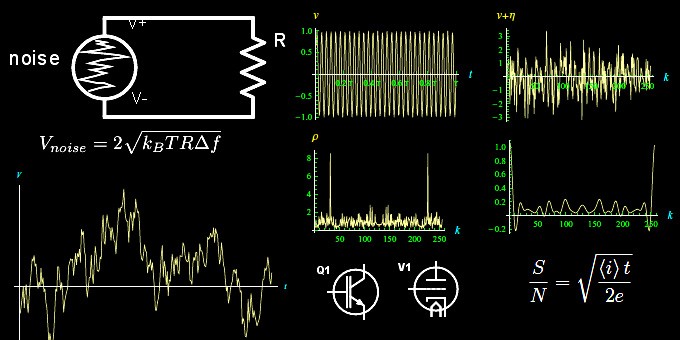
Immaginiamo di avere un amplificatore audio ad alto guadagno, a cui non è applicato alcun segnale d'ingresso. Collegando l'uscita a un altoparlante, si ascolta comunque un debole fruscio. Se proviamo a sostituire l'altoparlante con un oscilloscopio, osserviamo un andamento molto simile a quello riportato in figura 1.
Di cosa si tratta
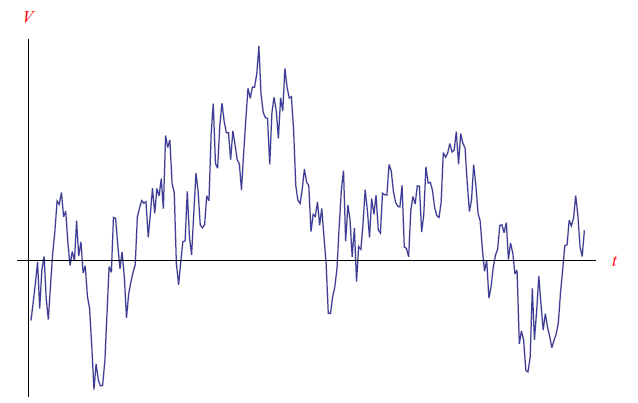
Figura 1. Tipico andamento della tensione di uscita in un amplificatore ad alto guadagno, in assenza di segnale di ingresso.
Abbiamo, dunque, un segnale in uscita con un andamento piuttosto irregolare, tecnicamente noto come rumore (in parte trattato in questo precedente articolo). Si tratta di un processo che emerge da processi legati a fluttuazioni spontanee di costituenti sub-microscopici (si pensi, ad esempio, agli elettroni). In alcuni casi tali fluttuazioni sono generate dall'agitazione termica per cui ci si aspetta un aumento del livello di rumore al crescere della temperatura di lavoro dei componenti dell'amplificatore.
Matematicamente, il rumore è un processo aleatorio stazionario. Con tale locuzione si intende una grandezza fisica che varia casualmente nel tempo, ma con un valor medio costante. Nel caso dell'amplificatore, ciò può essere constatato alzando o abbassando il controllo del guadagno. Il carattere aleatorio del rumore ci costringe a distinguere i segnali per così dire, "regolari" ovvero deterministici, da quelli non deterministici i.e. aleatori. Il principale strumento matematico di indagine è ovviamente la trasformata di Fourier. Tuttavia, nel caso dei segnali aleatori c'è la complicazione derivante dalla non conoscenza dell'espressione analitica del segnale assegnato. Si cerca allora di determinare lo spettro di potenza del rumore che permette - attraverso un noto teorema - di determinare la funzione di autocorrelazione ed in ultima istanza l'andamento temporale del rumore medesimo.
Introduzione
Consideriamo un circuito elettrico costituito da una resistenza ohmica R sottoposta a una differenza di potenziale assegnata. Tale grandezza può essere costante o variabile nel tempo t, per cui la corrente che attraversa R è:
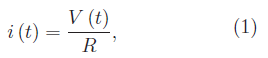
essendo V(t) la predetta d.d.p. In particolare, possiamo avere una funzione periodica di periodo T:
o non periodica, ma sufficientemente regolare:
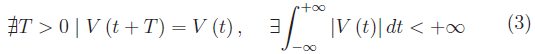
Come è noto, per lo studio di una rete lineare quale è quella assegnata, si applica il formalismo dell'Analisi di Fourier (trattata in un precedente articolo). In particolare, nel caso periodico si sviluppa V(t) in serie di Fourier che in notazione complessa si scrive:
Dalla (1):
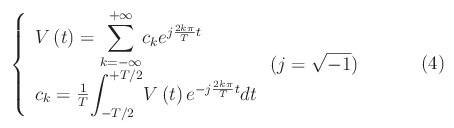
rammentando che al termine dei calcoli dobbiamo prendere la parte reale del secondo membro della (5) troncato a un assegnato ordine N di approssimazione:
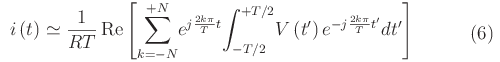
Osservazione
Si badi a non confondere il simbolo T del periodo con quello della temperatura assoluta T, che utilizzeremo in seguito.
Nel caso non periodico sviluppiamo V(t) in integrale di Fourier:
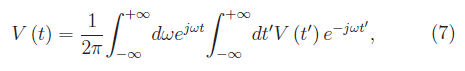
cosicché la corrente che attraversa la resistenza si scrive:
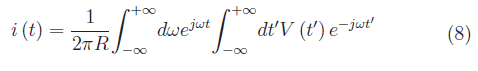
È fondamentale comprendere il ruolo svolto dalla funzione:
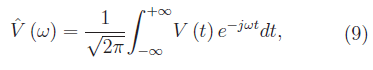
ovvero dalla trasformata di Fourier di V(t), nota anche come densità spettrale di V(t), giacché lo sviluppo integrale:
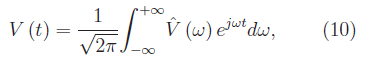
esprime V(t) attraverso una sovrapposizione lineare di infinite componenti sinusoidali
di ampiezza infinitesima:
Più precisamente, per un'assegnata frequenza angolare ω₁, la grandezza
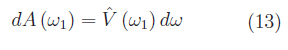
è l'ampiezza delle componenti di Fourier di frequenza ω appartenente all'intervallo infinitesimo [ω₁,ω₁+dω]. Ne consegue che la funzione reale:
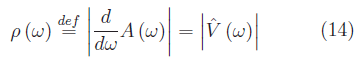
è l'ampiezza delle componenti di Fourier per intervallo unitario di frequenza. Da qui la denominazione densità spettrale per tale grandezza. Nel sistema S.I. misuriamo la d.d.p. in Volt (V ) e il tempo in secondi (s ), per cui segue dalla (9) che V(ω) e quindi ρ(s), si misura in V/Hz . Consideriamo ora la funzione reale:
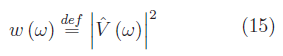
Per esplicitare il significato fisico della (15) riprendiamo il circuito con una sola resistenza R sottoposta alla d.d.p. V(t). La potenza dissipata per effetto Joule è:
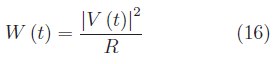
Per determinare il valor medio nel tempo di W(t), fissiamo un intervallo di tempo Δt>0, per cui il valore medio di W(t) in tale intervallo è:
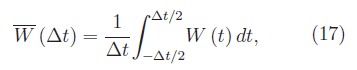
che è una funzione di %Delta;t. Quindi il valor medio in (-oo,+oo) della potenza W(t) è:
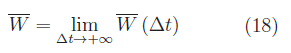
Dalla (16) segue
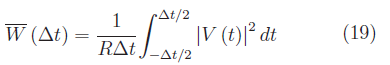
D'altra parte, per definizione di potenza:
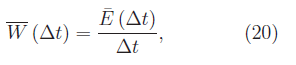
dove il termine a numeratore al secondo membro è è l'energia media nell'intervallo Δt. Segue:
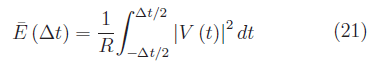
Eseguendo il limite per Δt->+oo otteniamo l'energia media nell'intervallo di tempo (-oo,+oo):
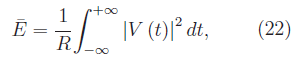
che è anche denominata energia totale del segnale elettrico V(t). Per l'uguaglianza di Parseval (trattata in un documento in Rete):
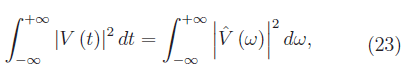
e tenendo conto della (15):
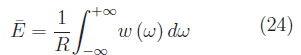
In altri termini, la grandezza (15) definisce lo spettro dell'energia media sviluppata dalla resistenza unitaria. Tale densità spettrale è impropriamente denominata spettro di potenza del segnale V(t). Il caso matematicamente più semplice è quello di una oscillazione sinusoidale limitata nel tempo (trattato in un documento in Rete), come mostrato in figura 2.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2898 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.
Ti potrebbe interessare anche:
L’amplificatore operazionale nel design di circuiti elettronici
Riconoscimento dei gesti con Wio Terminal
La progettazione dei circuiti stampati militari e aerospaziali
Firmware 2.0 #20: IoT-Blockchain/Cryptocurrency
Progetto di un sistema di allarme di terremoti con Arduino – Parte 1
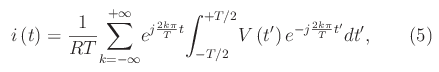
Da un punto di vista matematico, il noise è una variabile aleatoria. Quest’ultima può essere implementata nell’ambiente di calcolo Mathematica http://www.extrabyte.info/2017/03/06/un-approccio-computazionale-al-noise/
Complimenti per la trattazione, completa dalla matematica alla fisica a descrizione quantitativa e qualitativa delle componenti di rumore. Onestamente ho avuto un po’ di difficoltà a leggere l’articolo dall’inizio alla fine senza perdermi qualche passaggio, ma è un mio limite. Purtroppo ho lasciato queste dimostrazioni agli esami di analisi e teoria dei segnali risalenti a quasi dieci anni fa. Spesso, da ingegneri, riduciamo l’utilizzo di queste nozioni alla sola applicazione pratica delle formule finali, dimenticando, ahinoi, tutti i passaggi matematici e i vari teoremi che sono alla genesi di quelle formule. A volte però dico che raccapezzarsi con tutte quelle formule vuol dire fare un altro lavoro. Ecco il motivo per cui ben vengano articoli di questo calibro, per ricordare a noi lettori quanto sia prezioso il lavoro di matematici e fisici nel fornirci formule finali dall’applicazione tutto sommato semplificato. Grazie!
Articolo interessantissimo. I modelli matematici sono alla base dei fenomeni fisici sempre. Lo studio e l’analisi del rumore nei circuiti elettrici è un ambito di ricerca davvero importante, oltre che estremamente interessante. La riduzione del rumore è molto importante in applicazioni dove ad esempio il circuito viene utilizzato per il monitoraggio o la misurazione delle prestazioni di un altro dispositivo, e la presenza del rumore potrebbe indurre a effettuare misurazioni errate.
Grazie per le ottime recensioni!
Bell’articolo. Il rumore, solitamente è una componente di disturbo che va assolutamente eliminata dal sistema o, quantomeno, ridotta al massimo. Ma ci sono casi in cui una piccola quota di rumore viene aggiunta volutamente, per aumentare, ad esempio, il grado di risoluzione virtuale di una certa grandezza. Vedi, ad esempio, la digitalizzazione di un segnale elettrico a 8 bit, nel quale viene spesso aggiunto un noise attraverso un subsampling.
In alcuni casi il rumore è utilizzato in fisica per lo studio delle proprietà di un assegnato sistema. Da un punto di vista teorico, il primo step per lo studio del rumore è stato il moto browniano. Per chi vuole approfondire, c’è questo mio articolo http://www.extrabyte.info/moto_browniano_langevin.pdf
Ti riferisci alle tecniche di dithering e noise shaping applicate alla quantizzazione e ri-quantizzazione di segnali digitali? Effettivamente potrebbe sembrare strano come il peggior nemico dei sistemi elettronici talvolta sia voluto per aumentare la risoluzione di un segnale digitale precedentemente troncato a n bit. Eppure è così.
Giusto per curiosità, sembrerebbe che la prima intuizione sul dithering risalga ai tempi della seconda guerra mondiale, quando gli ingegneri notarono che i computer meccanici degli aeromobili funzionavano meglio in volo che a terra. La vibrazione dei motori portava in vibrazione le ruote dentate dei calcolatori meccanici schiodandole e facendole ruotare in maniera più fluida. Analogamente, è l’effetto che induce il rumore al segnale quantizzato.
Se ti riferisci al mio commento sulla possibilità di riscrivere la meccanica quantistica in termini di Teoria dei segnali, in realtà accennavo ad alcuni problemi interpretativi della fisica quantistica. Infatti, il principio di indeterminazione di Heisenberg impedisce di scrivere un’equazione oraria del tipo x=x(t) (particella che si muove sull’asse x), nel senso che l’ascissa x si comporta come una variabile aleatoria, con densità di probabilità pari al modulo quadro della “funzione d’onda” della particella.
La mia è probabilmente un’idea bislacca (cioè riscrivere la meccanica quantistica in termini di teoria dei segnali). Avevo scritto qualcos’altro qui http://www.extrabyte.info/quantum_computing000.pdf
Articolo interessante, Ho letto che addirittura il rumore bianco viene impiegato per scopi terapeutici, ad esempio per combattere l’insonnia. Sarebbe a questo punto sufficiente avere un amplificatore senza ingresso per ottenere un generatore di rumore bianco terapeutico?
si vendono su Amazon 🙂 https://tinyurl.com/y5zlshkc
Il rumore bianco è, in effetti, molto rilassante. Somiglia a quello della pioggia. Ma se non si fornisce una certa variazione random al rumore, diventa molto molto noioso e ripetitivo.
Inoltre, quando piove, il fisico e l’umore dell’Uomo stanno meglio, non tanto per il rumore prodotto dall’acqua, quanto alla quantità di Ioni negativi, molto benéfici per il corpo umano.
Si potrebbe tentare di riscrivere la Meccanica quantistica in termini di Teoria dei Segnali. Ad esempio, nel caso di una aprticella quantistica che compie un moto unidimensionale, l’ascissa x della particella è una variabile aleatoria la cui densità di probabilità è |psi(x,t)|^2, dove psi(x,t) è la funzione d’onda della particella (soluzione dell’equazione di Scrhödinger).
Idealmente, possiamo considerare uno “psi-metro” ossia uno strumento in grado di misurare la “densità di presenza” della particella. Realisticamente, uno psi-metro è un qualunque algoritmo risolutore della predetta eq. di Scrhödinger.
L’aspetto interessante è che l’ascissa della particella si comporta come un noise N, mentre l’ascissa della particella considerata come sistema classico (cioè che obbedisce alla meccanica classica) si comporta alla stregua di un segnale deterministico S. Quindi abbiamo la seguente corrispondenza:
S –> x(t)_classica
N –> x(t)_quantistica
http://www.extrabyte.info/2018/05/20/sistemi-quantistici-e-teoria-dei-segnali/