
Un controllo del livello d'acqua di un serbatoio utilizzando Simulink, un potente tool di MatLab per l'analisi e la progettazione di sistemi di controllo.
Uno schema possibile per il controllo d’acqua di un serbatoio è mostrato in figura 1 dove:
- Win(t) è la variabile di controllo del sistema (ovvero la variabile il cui valore è determinato dalla legge di controllo);
- h(t) è la variabile controllata (ovvero la variabile misurata e confrontata con un valore di riferimento assegnato);
- Wout(t) è una variabile esogena (prelievo da parte degli utenti);
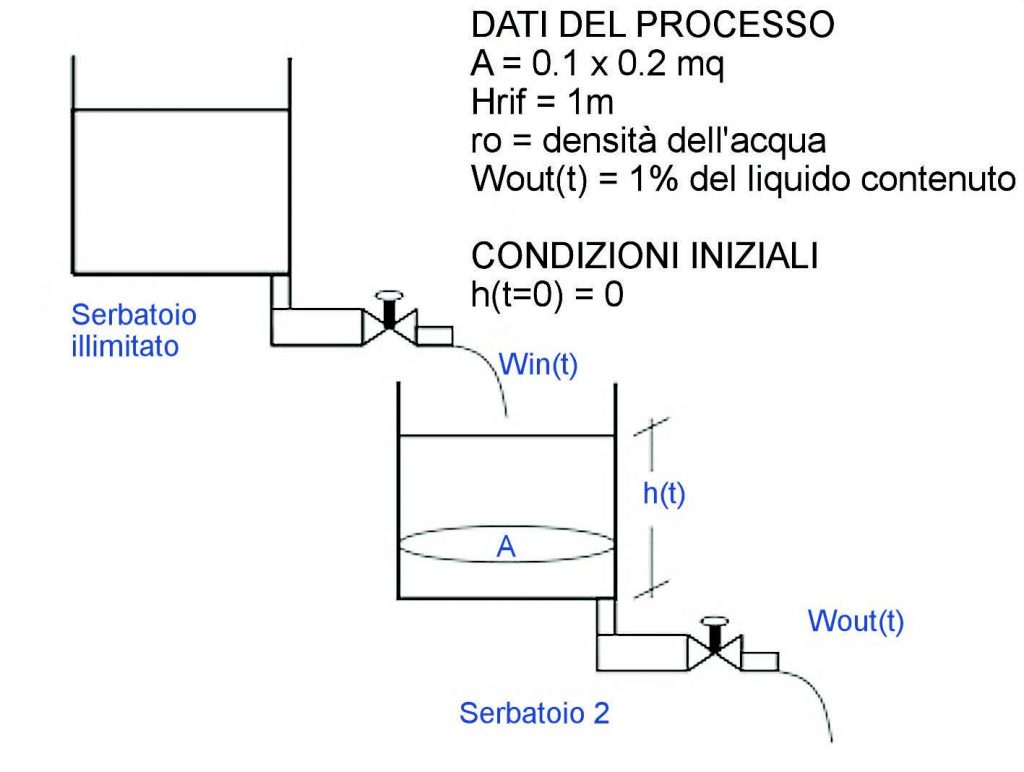
Figura 1: schema a blocchi.
In particolare mediante una opportuna regolazione è necessario garantire che il livello di acqua contenuto nel Serbatoio 2 sia sempre prossimo al livello massimo di 1m, affinché alle utenze sia possibile prelevare la quantità di acqua desiderata senza rischiare di svuotare il serbatoio stesso. L’equazione differenziale di bilancio a coefficienti costanti che descrive la dinamica del processo è:
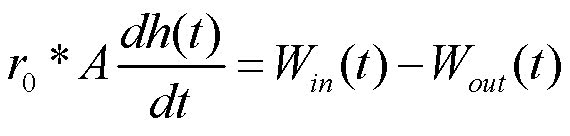
Trasformando tale equazione secondo Laplace diventa:
![]()
da cui si ricava la seguente funzione di trasferimento:
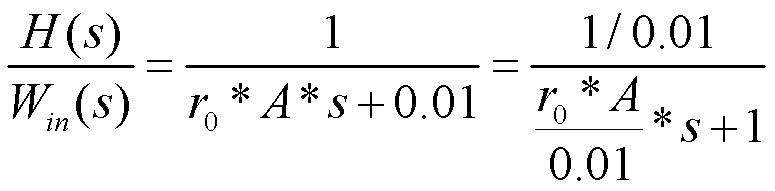
Con guadagno della funzione di trasferimento G = 102 costante di tempo della funzione di trasferimento Tm = 2*103 sec. tempo di assestamento della funzione di trasferimento TA = 5*Tm
Lo schema di Controllo in retroazione è quello di figura 2.
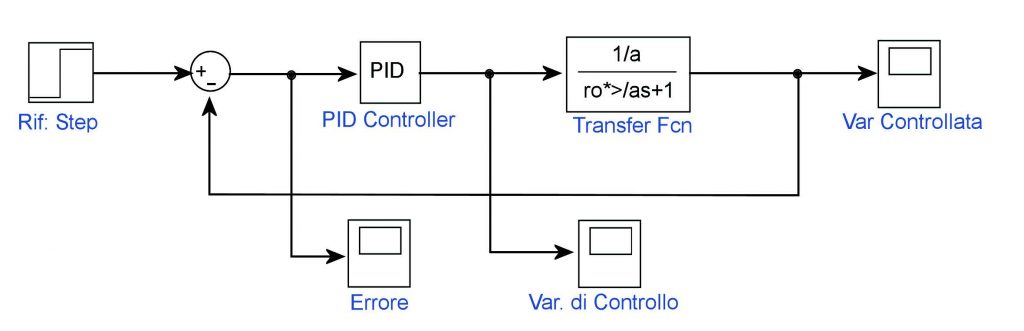
Figura 2: schema di controllo.
In particolare il blocco PID già implementato in Simulink è possibile trovarlo nel Simulink Library Browser seguendo il percorso Simulink Extras\Additional Linear\PID Controller. Affinché le specifiche del sistema siano soddisfatte (supponiamo che sia stato richiesto un TA = Tempo di Assestamento di circa 5 sec.) sarà quindi necessario tarare opportunamente i parametri Kp, Ki e (se necessario) Kd caratteristici del nostro Regolatore PID. In generale è possibile affrontare il problema del controllo utilizzando due approcci differenti: la Simulazione come Unico Strumento di controllo e la Simulazione come supporto al controllo.
SIMULAZIONE COME SUPPORTO
Basandosi sulle FdT (se disponibili) descrittive il Modello del Sistema ed il Regolatore utilizzato, è possibile calcolare analiticamente i parametri (Guadagno, Costante di Tempo Dominante, ecc.) che definiscono la Funzione di Anello Chiuso del Sistema Retroazionato e che dipendono dai coefficienti del Regolatore implementato. Al fine di soddisfare le specifiche di progetto tali parametri dovranno assumere specifici valori medianti i quali risalire alla rispettiva taratura del regolatore.
SIMULAZIONE COME UNICO STRUMENTO
Mediante una valutazione grafica del comportamento modulante della Variabile Controllata è possibile ricavare le informazioni essenziali al fine di comprendere:
- il Tempo di Assestamento del Sistema Controllato e quindi la rispettiva Costante di Tempo Dominante;
- il Guadagno della FdT, ecc...
Tarando quindi opportunamente i parametri di regolazione è possibile ottenere l’andamento desiderato nel rispetto delle specifiche di progetto fornite e verificarne graficamente la coerenza a seguito di ogni modifica. Supponiamo di voler applicare una cancellazione perfetta con un regolatore PI: ricordando la funzione di trasferimento del regolatore PI:
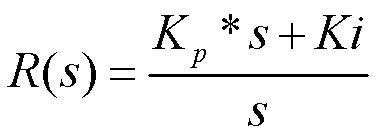
risulta Kp=2000 e Ki = 1. Nelle figure 3 e 4 le simulazioni relative agli andamenti dell’errore, della variabile di controllo e della variabile controllata.
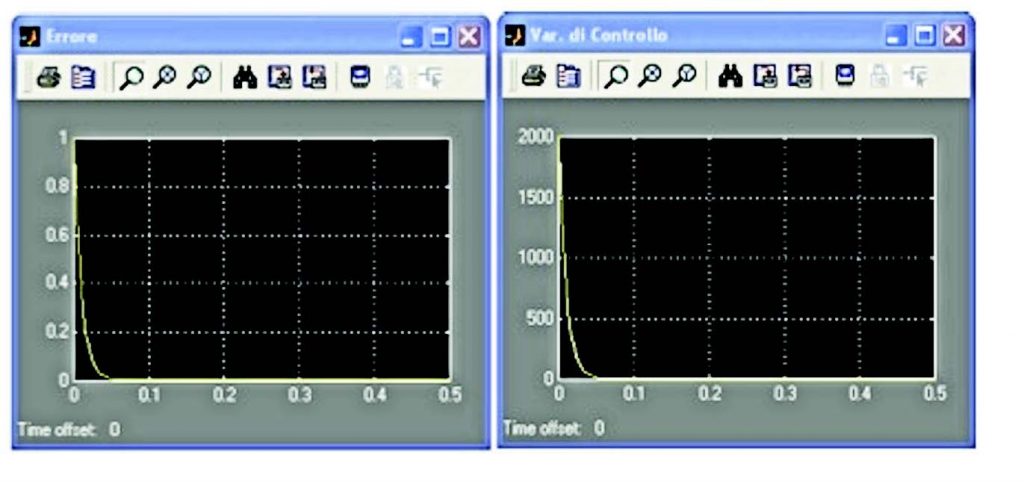
Figura 3: errore e variabile di controllo
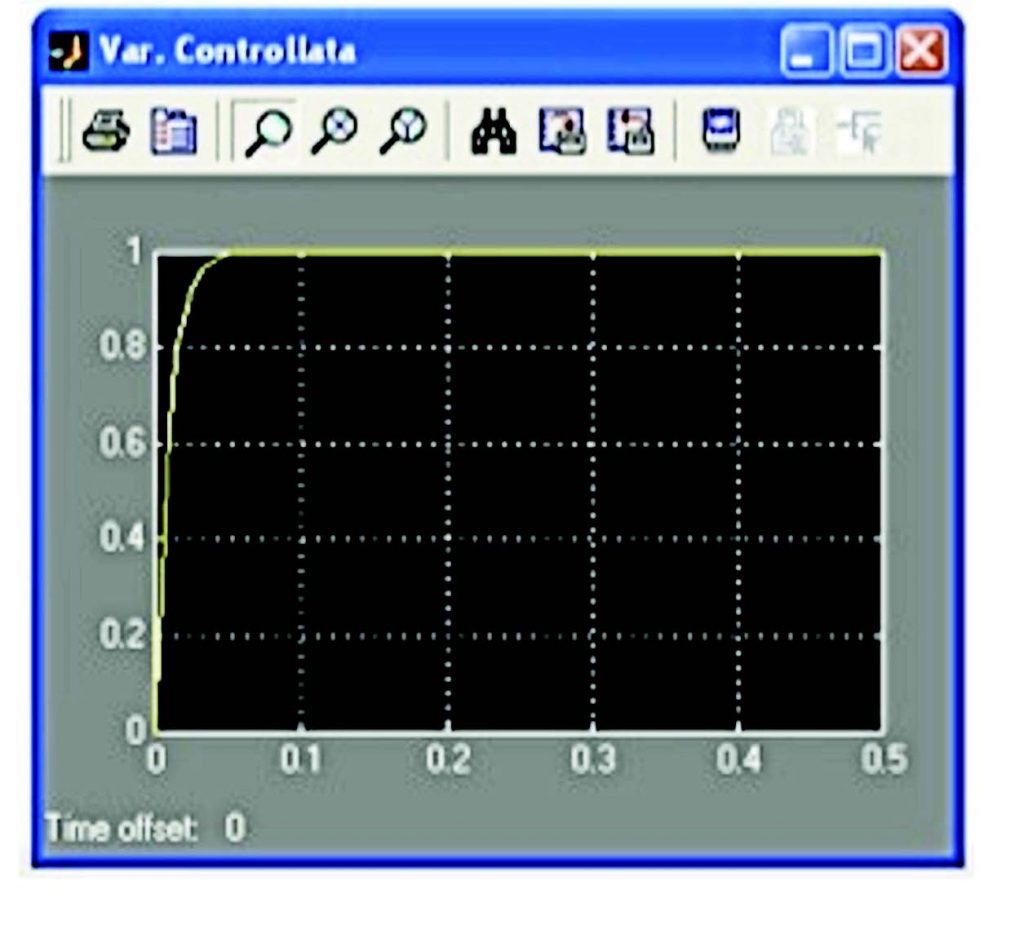
Figura 4: variabile controllata.
Come è possibile notare la variabile di controllo rispetta le specifiche richieste (TA<5sec.) e assume un andamento del tutto favorevole, che non presenta infatti oscillazioni o sovra/sotto-elongazioni. Tuttavia non bisogna trascurare il fatto che la variabile di controllo deve assumere valori molto elevati. E’ necessario rivedere quindi la taratura del Regolatore affinché, pur continuando a soddisfare le specifiche, non debba essere soggetto a sforzi così elevati. Grazie a questo tipo di regolazione le specifiche sono ancora una volta soddisfatte con il vantaggio che ora la variabile di controllo assume valori più contenuti.
REGOLATORI PID
Controllare un sistema vuol dire quindi effettuare una regolazione su di esso, regolazione che può essere effettuata con tecniche diverse. Infatti i sistemi possono essere controllati adottando i seguenti metodi di regolazione:
- Regolatori ad AZIONE PROPORZIONALE (P)
- Regolatori ad AZIONE INTEGRATIVA (I)
- Regolatori ad AZIONE PROPORZIONALE-INTEGRATIVA (PI)
- Regolatori ad AZIONE PROPORZIONALE-DERIVATIVA (PD)
- Regolatori ad AZIONE PROPORZIONALE-NTEGRATIVA-DERIVATIVA (PID).
L’azione effettuata da un regolatore PID avviene in tre tempi: prima si attiva una regolazione di tipo derivativa, poi subentra la regolazione proporzionale ed infine la regolazione integrativa. La legge che identifica tale schema è la seguente:
a(t) = Kp e(t) + Ki ò e(t) dt + Kd de(t)/dt
dove troviamo Kp che indica il guadagno del regolatore proporzionale, e(t) rappresenta il segnale errore, Ki indica il guadagno del regolatore integrativo, Kd indica il guadagno del regolatore derivativo. L’azione operata dal regolatore PID è quella di inserire nel sistema un polo nell’origine (aumentando quindi il tipo) e due zeri (che contribuiscono a migliorare la stabilità), i quali sono normalmente reali e distinti.
ALTRI MODELLI SIMULINK
Analizziamo alcuni esempi di modelli Simulink:
- Modello “termico” per casa.
Il modello visualizzato in figura 5 fornisce la possibilità di gestire le variabile ambientali e il sistema di riscaldamento della casa.
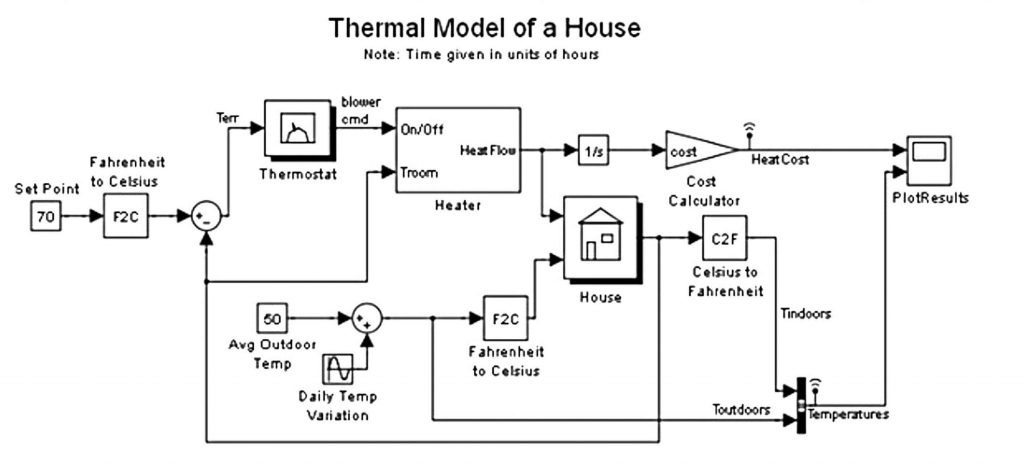
Figura 5: modello termico della casa.
I componenti principali sono:
- Set point: specificata la temperatura che deve essere mantenuta nella casa.
- Thermostat: è un blocco di ritardo. Permette fluttuazioni di 5 gradi fahrenheit sopra o sotto la temperatura desiderata.
- Heater: è il blocco di riscaldamento. Modello Contatore con flip flop.
Il modello in esame visualizzato in figura 6 fa vedere come usare un blocco flip flop per la realizzazione di un contatore.
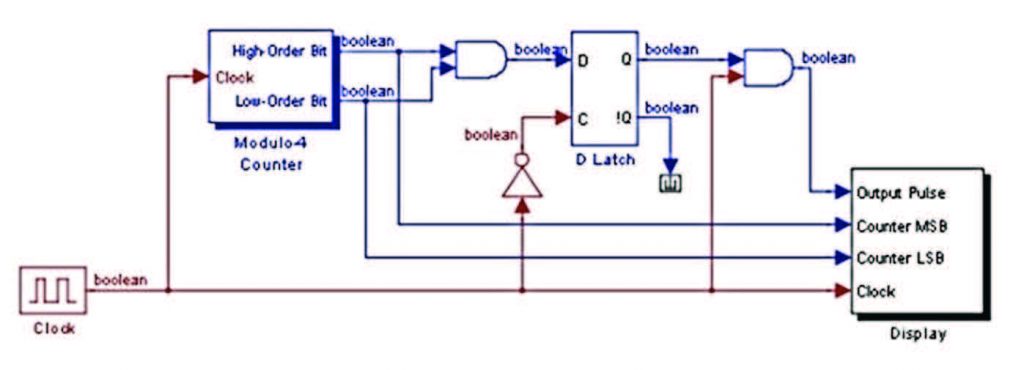
Figura 6: contatore.
Il principio base è semplice, l’andamento dei segnali è rappresentato in figura 7. I flip-flop (o bistabili) sono circuiti elettronici molto semplici, utilizzati nell’elettronica digitale come dispositivi di memoria elementare. Il nome Flip-Flop deriva dal rumore che facevano i primi circuiti di questo tipo, costruiti con relè che permettevano il cambiamento di stato.
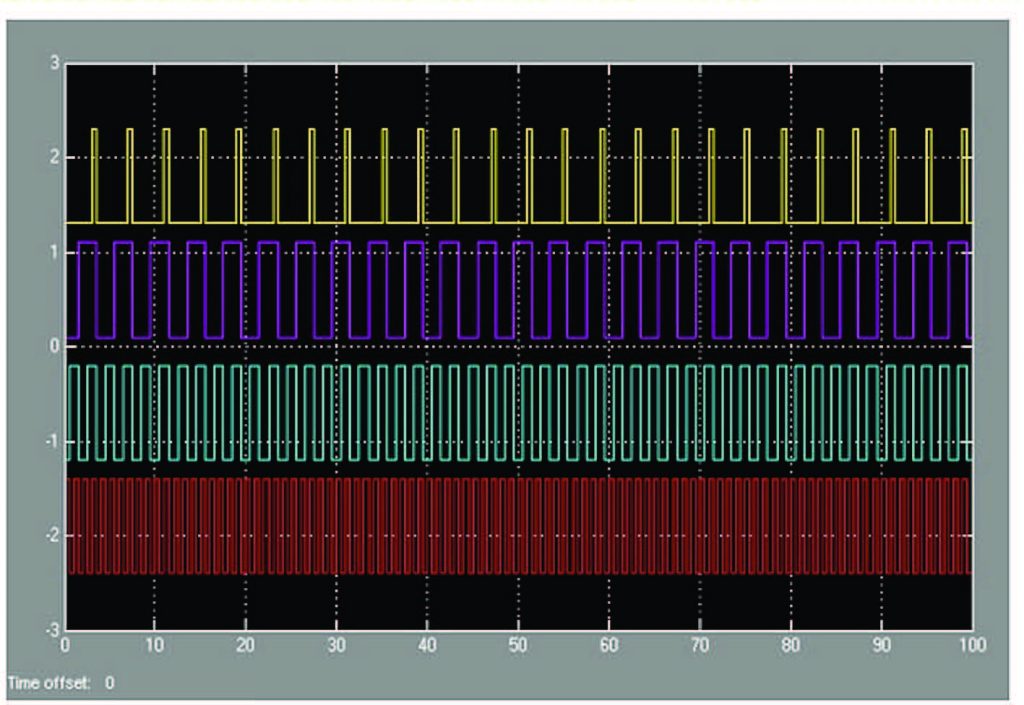
Figura 7: segnali digitali del contatore.





Tempo fa un cliente mi chiese tale applicazione….. esistono, in effetti, tantissimi modi per implementarlo.