Corso di Elettronica per ragazzi – Puntata 12

Nel precedente articolo, “Corso di Elettronica per ragazzi - Puntata 11”, abbiamo descritto e analizzato un semplice circuito di esempio costituito da tre elementi in parallelo: un generatore di corrente controllato in corrente, un generatore indipendente di corrente e un resistore di cui abbiamo calcolato la corrente e la tensione ai suoi capi e anche eseguito la simulazione. Abbiamo poi descritto il concetto di resistenza equivalente di un circuito resistivo e spiegato come calcolarla. Inoltre, abbiamo dato la definizione di due importanti teoremi, ovvero il teorema di Thevenin e il teorema di Norton. Infine, nella sua prima parte, abbiamo introdotto l’amplificatore di corrente descrivendone il modello e lo schema completo. In questo articolo, faremo un esempio di un circuito mediante il quale approfondiremo i teoremi di Thevenin e Norton spiegando come ottenere i rispettivi circuiti equivalenti di parti circuitali. Infine, con la seconda parte, riprenderemo l’analisi dell’amplificatore di corrente con un esempio applicativo.

Introduzione - I teoremi di Thevenin e Norton

Le basi della teoria dei circuiti lineari (come i circuiti resistivi) poggiano sulla teoria dell'elettromagnetismo di Maxwell (di cui parleremo in un’altra puntata). Nella sua forma più applicativa, la teoria dei circuiti si basa sui concetti fondamentali delle leggi di Kirchoff, Legge di Ohm, impedenza e Principio di Sovrapposizione (che tratteremo nella prossima puntata). Da questa base, qualsiasi circuito lineare può essere risolto una volta nota la specifica di tutte le sorgenti presenti nel circuito (generatori indipendenti di tensione e di corrente), ovvero è possibile trovare e risolvere un insieme di equazioni lineari (equazione algebrica di primo grado in cui l’esponente dell’incognita è 1, ad esempio, 2x(1)+3=0) per ricavare qualsiasi tensione e corrente nel circuito. Uno dei più rilevanti concetti derivanti dalla teoria dei circuiti lineari è il circuito equivalente (di cui abbiamo già parlato nelle precedenti puntate), ossia un circuito semplificato di un circuito complesso, da qualsiasi coppia di terminali venga considerato, che si comporta come se consistesse solo di una sola sorgente e di una sola resistenza, rispettivamente denominati “generatore equivalente” e “resistenza equivalente” (in generale, impedenza equivalente). In sostanza, il concetto di circuito equivalente semplifica i calcoli nella teoria dei circuiti e mette in primo piano le impedenze di ingresso e di uscita di un circuito. Più in generale, la nozione di circuito equivalente significa ottenere un circuito più semplice, ma funzionalmente in una forma equivalente ai sistemi circuitali complicati. Nel concetto di circuito equivalente, predominano il circuito equivalente di Thevenin e il circuito equivalente di Norton. Come mostrato nella Figura 1, i due circuiti equivalenti differiscono solo per il tipo di sorgente: di tensione, per il circuito equivalente di Thevenin (Figura 1a), di corrente, per il circuito equivalente di Norton (Figura 1b).

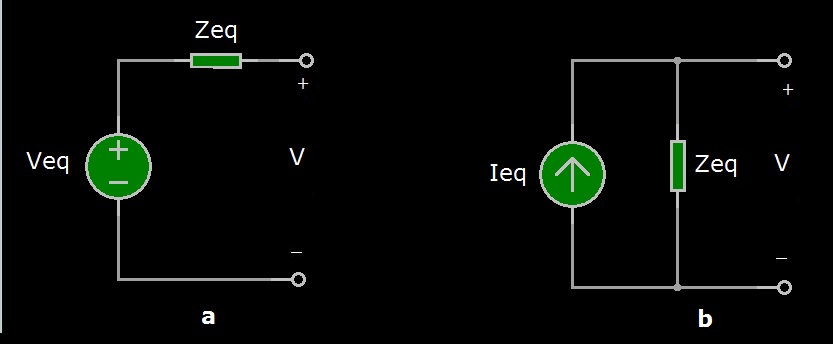
Figura 1: Circuito equivalente di Thevenin (a) e di Norton (b)

La resistenza equivalente Req, o impedenza equivalente Zeq, è la stessa in entrambi i casi, e i valori delle sorgenti sono correlati tra loro dalla relazione Veq=Zeq*Ieq.

Esercitazione teorica

Utilizziamo il circuito di esempio di Figura 2 per ottenere il circuito equivalente di Thevenin e di Norton di una parte del circuito.

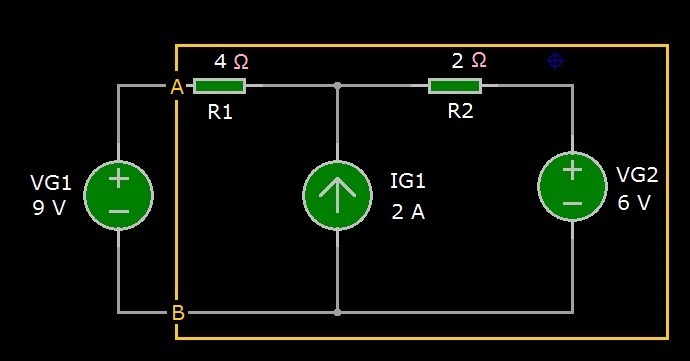
Figura 2: Circuito di esempio per l’esercitazione teorica

In questa esercitazione teorica, vogliamo ricavare il circuito equivalente di Thevenin e di Norton della parte di circuito inclusa nel rettangolo dal punto di vista dei terminali A-B. Questo circuito è costituito da due generatori indipendenti di tensione VG1 e VG2, un generatore indipendente di corrente IG1, due resistori R1 e R2.

Il circuito equivalente di Thevenin

Per la nostra esercitazione teorica, innanzitutto riportiamo la definizione del teorema di Thevenin:

Il teorema di Thevenin afferma che un qualsiasi circuito resistivo è equivalente ad un generatore indipendente di tensione e una resistenza in serie. Il valore di tensione del generatore corrisponde alla tensione a vuoto (a circuito aperto) calcolata ai capi dei due terminali del circuito, mentre il valore della resistenza è la resistenza equivalente del circuito calcolata con tutti i generatori indipendenti spenti.

Quindi, il circuito equivalente di Thevenin è costituito da un generatore indipendente di tensione, che chiamiamo Veq, con in serie una resistenza che chiamiamo Req. Il valore della tensione Veq (che sarà poi il valore del generatore di Thevenin) viene determinato calcolando la tensione ai capi di A e B a circuito aperto (o a vuoto), ossia scollegando dal circuito, ai terminali A-B, il generatore VG1 da 9V, come illustrato in Figura 3.

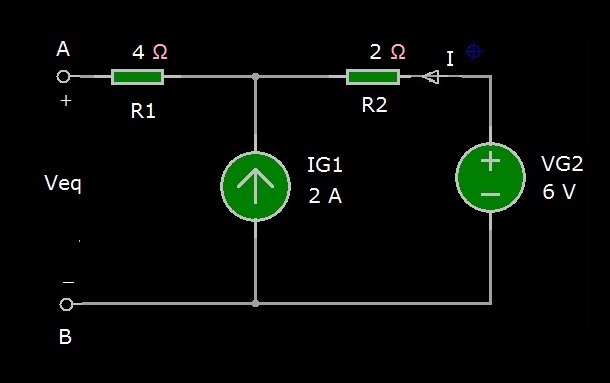
Figura 3: Circuito per il calcolo di Veq di Thevenin

Essendo scollegata dal circuito, nella resistenza R1 non circola corrente, pertanto non avviene caduta di tensione ai suoi capi. Quindi, la tensione Veq corrisponde esattamente alla tensione ai capi del generatore di corrente IG1. Applicando la LKT (Legge di Kirchhoff delle tensioni) alla maglia VG2-R2-Veq, e nominando con I la corrente che scorre in R2, si ha la seguente equazione:

VG2-R2*I-Veq=0 Essendo I=-IG1 VG2+R2*IG1-Veq=0

Ora ricaviamo Veq dalla precedente relazione:

Veq= VG2+R2*IG1=6+4=10 V

Calcolato il generatore equivalente Veq, a questo punto, per completare il circuito equivalente di Thevenin, occorre determinare la resistenza equivalente del circuito di Figura 3, che calcoleremo con tutti i generatori indipendenti spenti (per generatori spenti equivale a considerare un corto circuito, il generatore indipendente di tensione VG2, e un circuito aperto, il generatore indipendente di corrente IG1). Il circuito risultante è mostrato in Figura 4.

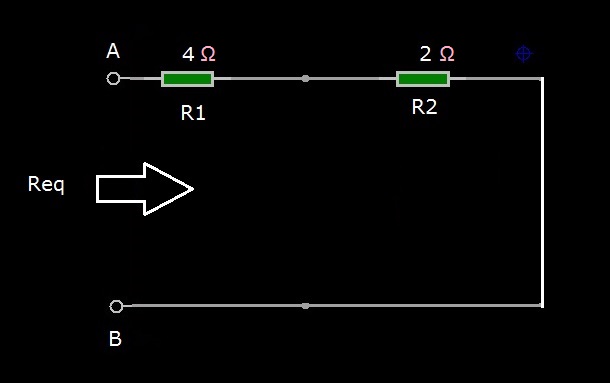
Figura 4: Circuito con i generatori spenti

Il circuito risultante è costituito dai due resistori R1 e R2 in serie, quindi, calcolare Req vista dai terminali A e B è ora molto semplice:

Req=R1+R2=6 ohm

Ora, possiamo ridisegnare come in Figura 5 il circuito di Figura 2, ora più semplice grazie al circuito equivalente di Thevenin!

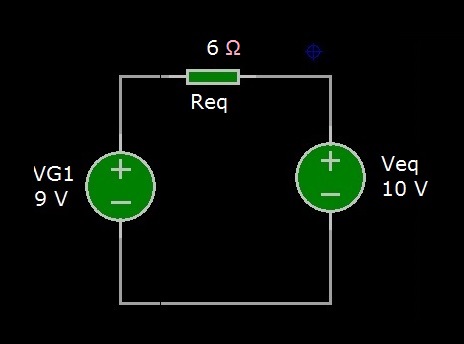
Figura 5: Circuito semplificato con Thevenin

Esercitazione teorica con Norton

Il circuito del nostro esempio può essere semplificato anche calcolando il circuito equivalente di Norton. Di seguito riportiamo la definizione del teorema di Norton.

Il teorema di Norton afferma che un qualsiasi circuito resistivo è equivalente ad un generatore indipendente di corrente con una resistenza in parallelo. Il valore di corrente del generatore corrisponde alla corrente che fluisce attraverso i due terminali del circuito posti in corto circuito, mentre il valore della resistenza corrisponde alla resistenza equivalente del circuito calcolata con tutti i generatori indipendenti spenti.

Riprendendo lo schema elettrico del circuito equivalente di Thevenin che abbiamo calcolato prima e applicando il teorema di Norton, come mostrato in Figura 6, possiamo vedere la correlazione dei due circuiti equivalenti.

[...]

ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 2407 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.