In questa puntata, ci occuperemo ancora di amplificatori operazionali eseguendo il calcolo di alcuni circuiti in cui, in un caso l’operazionale è configurato come amplificatore non invertente, e in un altro caso come amplificatore invertente. In questi esercizi, vedremo che i circuiti saranno un pò più complessi rispetto alle configurazioni invertenti e non invertenti di base. L’amplificatore operazionale in questi circuiti sarà considerato ideale. Ciò ci semplificherà notevolmente i calcoli, d’altronde, come abbiamo constatato nella precedente Puntata 21, l’errore di calcolo di un circuito con operazionale ideale rispetto all’operazionale reale è irrilevante. Infine, tratteremo l’argomento “Amplificatori operazionali in cascata” di cui faremo anche un’esercitazione in cui vedremo come calcolare la tensione di uscita e l’amplificazione di tensione di un circuito costituito da due stadi operazionali in cascata.
Esercitazione 1 - Calcolo della tensione di uscita di un amplificatore non invertente
Nel circuito descritto nello schema elettrico di Figura 1 vogliamo calcolare la tensione di uscita Vo dell’amplificatore operazionale in configurazione non invertente. All’ingresso dell’amplificatore è collegato un generatore indipendente di tensione Vin.
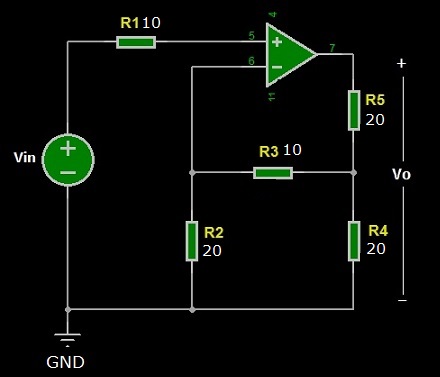
Figura 1: Schema dell’amplificatore operazionale non invertente
Il circuito equivalente dell’amplificatore operazionale ideale
Prima di iniziare il calcolo del circuito, faremo un riepilogo sul circuito equivalente di un amplificatore operazionale ideale mostrato in Figura 2.
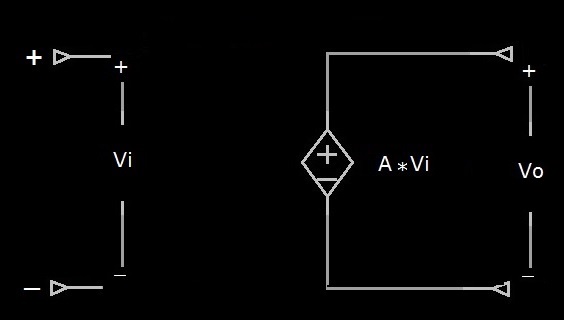
Figura 2: Circuito equivalente dell’amplificatore operazionale ideale
Notiamo che il circuito d’ingresso è aperto, ossia ai terminali + e - dell’operazionale non è presente alcun elemento, quindi possiamo dire che la resistenza d’ingresso è infinita, mentre è presente una tensione Vi.
Riguardo al circuito di uscita, in serie al generatore controllato A*Vi la resistenza è nulla, quindi, applicando la LKV alla maglia A*Vi-Vo si ottiene l’espressione seguente:
A*Vi-Vo=0
Da cui ricaviamo Vi=Vo/A
Essendo ideale l’operazionale, l’amplificazione di tensione ad anello aperto A è infinita, ossia A=∞, pertanto:
Vi=V(+)-V(-)=Vo/∞=0
Quindi, la tensione Vi ai terminali + e - dell’operazionale è nulla.
Da quanto fin qui esposto, scaturiscono le seguenti affermazioni:
1) non può scorrere corrente nei terminali d’ingresso + e - dell’operazionale;
2) dato che la tensione d’ingresso dell’operazionale Vi=0, allora i terminali + e – sono allo stesso potenziale, quindi è come se fossero in cortocircuito fisico, ma noi diciamo che sono in cortocircuito virtuale, ovvero qualsiasi cosa collegata al terminale positivo si considera che sia collegata anche al terminale negativo dell’operazionale.
Abbiamo voluto riportare questi passaggi relativi al circuito equivalente per ribadire due importanti concetti da considerare nell’analisi del circuito di Figura 3 in cui sono stati indicati i versi delle correnti e delle tensioni.
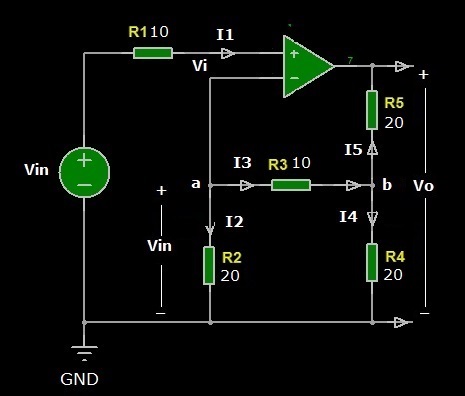
Figura 3: Schema dell’amplificatore non invertente
Per giungere alla soluzione dell’esercitazione, ossia al risultato del calcolo della tensione di uscita Vo dell’amplificatore, utilizzeremo l’analisi nodale tenendo presente quanto segue:
1) la corrente I1=0, quindi, dalla legge di Ohm, VR1=R1*I1=0.
Non essendoci caduta di tensione su R1, il generatore di tensione Vin risulta applicato direttamente fra il terminale positivo (+) dell’operazionale e terra (GND).
2) il generatore di tensione Vin collegato fra il terminale positivo (+) dell’operazionale e terra (GND), per il cortocircuito virtuale dei terminali + e - , si trova applicato anche fra il terminale negativo (-) dell’operazionale e terra, ovvero la tensione Vin è presente ai capi del resistore R2.
Premesso quanto esposto sopra, innanzitutto applichiamo la LKC al nodo “a” e consideriamo positive le correnti uscenti dal nodo:
I2+I3=0
Con la legge di Ohm calcoliamo la corrente I2 indicando con “Va” la tensione fra il nodo “a” e terra:
I2=Va/R2
Calcoliamo la corrente I3 applicando la LKV alla maglia Va-R3-Vb in cui “Vb” è la tensione fra il nodo “b” e terra:
Va-R3*I3-Vb=0 => R3*I3=Va-Vb => I3=(Va-Vb)/R3
Sostituiamo I2 e I3 nell’espressione delle correnti:
1) Va/R2+(Va-Vb)/R3=0
Ora applichiamo la LKC al nodo “b”:
-I3+I4+I5=0
La I3 è già stata calcolata, quindi calcoliamo le correnti I4 e I5:
I4= Vb/R4
Per calcolare la corrente I5 applichiamo la LKV alla maglia R4-R5-Vo, tenendo conto del verso delle correnti e delle tensioni:
Vb-R5*I5-Vo=0 => R5*I5=Vb-Vo => I5=(Vb-Vo)/R5
Sostituiamo I3, I4 e I5 nell’espressione delle correnti:
2) -(Va-Vb)/R3+Vb/R4+(Vb-Vo)/R5=0
Dalle precedenti considerazioni sappiamo che Va coincide con Vin: Va≡Vin, quindi andiamo a sostituire Va con Vin nelle precedenti espressioni 1) e 2) calcolate delle correnti:
Per il cortocircuito virtuale, Vi=V(+) - V(-)=0, ossia V(+)=V(-),
V(-)=Va=Vin.
1) Vin/R2+(Vin-Vb)/R3=0
2) -(Vin-Vb)/R3+Vb/R4+(Vb-Vo)/R5=0
Ora ricaviamo Vb dall’equazione 1) e la sostituiamo nella 2):
1) Vin/R2+(Vin-Vb)/R3=0
Vin/R2+Vin/R3-Vb/R3=0 => Vin*(1/R2+1/R3)-Vb/R3=0
Sostituiamo il valore di resistenza ai simboli dei resistori e svolgiamo le operazioni:
=> Vin*0,15-Vb*0,1=0 => Vb=Vin*0,15/0,1=1,5*Vin
Nella seguente relazione 2) svolgiamo le parentesi:
2) -(Vin-Vb)/R3+Vb/R4+(Vb-Vo)/R5=0
Vb/R3-Vin/R3+Vb/R4+Vb/R5-Vo/R5=0
Mettendo in evidenza Vb si ha:
Vb*(1/R3+1/R41/R5)-Vin/R3-Vo/R5=0
Ora isoliamo a sinistra del segno di uguaglianza il termine con Vo per calcolare Vo:
Vo/R5= Vb*(1/R3+1/R41/R5)-Vin/R3 =>
=> Vo=[Vb*(1/R3+1/R4+1/R5)-Vin/R3]*R5 =>
=> Vo=Vb*R5*(1/R3+1/R4+1/R5)-Vin*R5/R3
Sostituiamo Vb=1,5*Vin e gli altri simboli con i valori numerici:
Vo=Vin[1,5*20*(0,1+0,05+0,05)-(20/10)] =>
Vo=Vin(30*0,2-2)=4 V
Quindi, la tensione di uscita Vo dell’amplificatore non invertente è:
Vo=4*Vin
Si noti che la tensione di uscita Vo ha lo stesso segno positivo della tensione d’ingresso Vin; ciò dimostra la caratteristica dell’amplificatore non invertente.
Da questa relazione ricaviamo facilmente l’amplificazione di tensione ad anello chiuso, ossia il rapporto fra la tensione di uscita e la tensione del generatore di tensione Vin applicata all’ingresso dell’amplificatore:
Av=Vo/Vin=4
Esercitazione 2 - Calcolo del guadagno di tensione ad anello chiuso di un amplificatore invertente
Lo schema elettrico di Figura 4 è un amplificatore invertente il cui circuito è costituito da un generatore di tensione applicato in ingresso, un amplificatore operazionale in configurazione invertente e alcuni elementi resistivi. In questa esercitazione, vogliamo calcolare il guadagno di tensione ad anello chiuso, ovvero l’amplificazione di tensione Av=Vo/Vin, considerando che Av sia 100 e la resistenza d’ingresso del circuito vogliamo che sia non inferiore a 1 MΩ (M=1000.000).
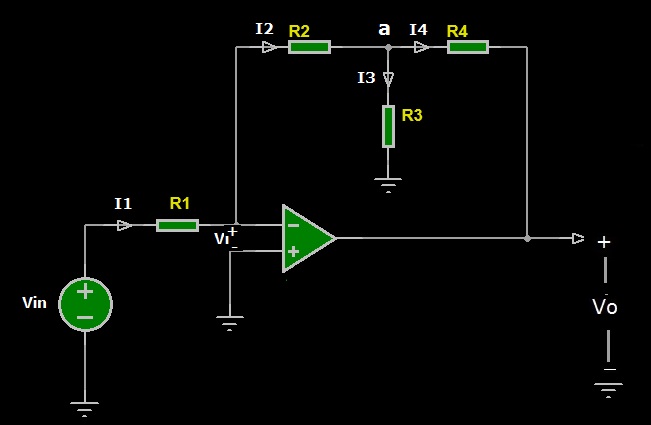
Figura 4: Schema elettrico dell’amplificatore invertente
Analizzando il circuito di Figura 4 possiamo intanto affermare che, essendo ideale l’operazionale, non scorre corrente nel terminale d’ingresso negativo (-). Pertanto, la corrente I1 è la stessa che scorre nel resistore R2, oltre che nel resistore R1. Stabilito questo, applichiamo la LKC al nodo “a” del circuito in cui decidiamo che questa volta siano positive le correnti entranti e negative quelle uscenti dal nodo “a”:
I2-I3-I4=0
Calcoliamo ognuna di queste correnti tenendo conto del loro verso e di quello delle tensioni:
I2=I1 e dato che dalla legge di ohm I1=Vin/R1 I2= Vin/R1
I3=Va/R3 (Va è la tensione fra il nodo ”a” e terra)
Per calcolare la corrente I4 applichiamo la LKV alla maglia Va-R4-Vo:
Va-R4*I4-Vo=0 => R4*I4=Va-Vo => I4=(Va-Vo)/R4
Quindi, riscriviamo la LKC al nodo “a” sostituendo le correnti calcolate prima:
Vin/R1-Va/R3-(Va-Vo)/R4=0
Svolgiamo le parentesi e poi mettiamo in evidenza Va:
1) Vin/R1-Va*(1/R3+1/R4)+Vo/R4=0
A questo punto, dobbiamo trovare una relazione per Va che nella precedente equazione (1) è un’incognita. Ricaviamo Va applicando la LKV alla maglia Vi-R2-Va:
Vi-R2*I2-Va=0
Sappiamo che Vi=0 e che la corrente I2=Vin/R1, quindi riscriviamo nuovamente la LKV sostituendo la I2:
0-R2*Vin/R1-Va=0
Ora, possiamo ricavare Va:
Va=-Vin*R2/R1
Calcolata Va, andiamo a sostituirla nella precedente equazione (1):
1) Vin/R1-Va*(1/R3+1/R4)+Vo/R4=0
Vin/R1-(-Vin*R2/R1)*(1/R3+1/R4)+Vo/R4=0
Mettiamo in evidenza Vin:
Vin*(1/R1+R2/R1)*(1/R3+1/R4)+Vo/R4=0
Isoliamo il termine con Vo e ricaviamo Vo:
Vo/R4=-Vin*(1/R1+R2/R1)*(1/R3+1/R4)
Vo=-Vin*(1/R1+R2/R1)*(1/R3+1/R4)*R4
Finalmente, dividendo i due membri dell’uguaglianza per Vin, calcoliamo l’amplificazione (o guadagno) di tensione ad anello chiuso dell’amplificatore invertente:
Av=Vo/Vin=-(1/R1+R2/R1)*(1/R3+1/R4)*R4
Av=-[(1+R2)/R1]*[(R3+R4)/(R3*R4)]*R4
Elidendo R4 dall’espressione, si ha l’equazione finale di Av:
Av=-[(1+R2)/R1]*[(R3+R4)/R3]
A questo punto, nella relazione del guadagno composta da due fattori, occorre definire i valori esatti dei resistori per soddisfare la richiesta dell’esercitazione, ossia un guadagno di 100 e una resistenza d’ingresso di 1 MΩ.
Partiamo dalla resistenza d’ingresso per poi definire di conseguenza gli altri valori di resistenza dei restanti resistori. Abbiamo visto nella Puntata 18 del corso che la resistenza d’ingresso di un amplificatore invertente è determinata dalla resistenza “vista” dalla sorgente di tensione d’ingresso dell’operazionale. Quindi, premettendo che imponiamo che i resistori di questo amplificatore non superino il valore di resistenza di 1 MΩ, decidiamo che la resistenza d’ingresso sia rappresentata dal resistore R1=1 MΩ. Stabilito il valore di R1 che appare nel primo fattore del prodotto della formula di Av, definiamo il valore di R2 in modo che questo fattore dia come risultato 1, ovvero R2=1 MΩ. A questo punto, non ci resta che fare in modo che il secondo fattore della formula di Av dia il risultato di 100 scegliendo i giusti valori di R3 e R4. In sostanza, deve essere (R3+R4)/R3=100. Definendo R4=1 MΩ (M=1000.000) e R3=10,1 KΩ (K=1000), sostituendo ai simboli i valori numerici possiamo constatare che il risultato del calcolo dell’amplificazione di tensione è proprio uguale in valore assoluto a 100:
Av=-(1+1M)/1M*(10,1K+1M)/10,1K=-100
Ovviamente, l’esatto valore di Av dipenderà dalla tolleranza di precisione della resistenza dei resistori. Notiamo che il risultato è negativo in quanto l’amplificatore invertente opera l’inversione di segno della tensione d’ingresso Vin applicata: se la tensione d’ingresso Vin è positiva, la tensione di uscita sarà negativa, mentre se la tensione d’ingresso Vin è negativa, la tensione di uscita sarà positiva.
Amplificatori operazionali in cascata
In vari casi applicativi può non essere sufficiente utilizzare un solo amplificatore operazionale in circuiti che richiedono prestazioni più alte. In questi casi, si ricorre all’impiego di più stadi operazionali collegati in cascata, ovvero collegando l’uscita di uno stadio all’ingresso dello stadio successivo. In Figura 5 è rappresentato lo schema a blocchi di esempio costituito da due stadi amplificatori operazionali non invertenti in cascata.
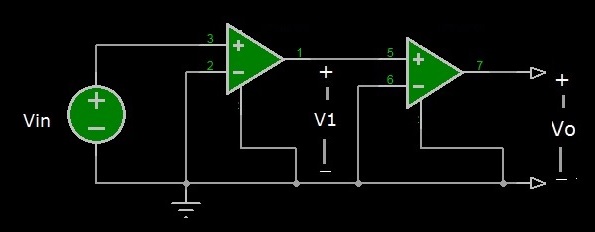
Figura 5: Schema a blocchi di due stadi in cascata
Ogni stadio amplificatore operazionale ha quattro terminali, due d’ingresso e due di uscita. All’ingresso del primo stadio è applicato un generatore di tensione. I circuiti degli stadi in cascata possono essere disegnati con operazionali configurati di base, ma possono anche essere più complessi, come quelli che abbiamo visto nelle esercitazioni 1 e 2. Nell’esempio che faremo di seguito, vedremo come si calcola la tensione di uscita e l’amplificazione di tensione di un circuito costituito da due amplificatori operazionali invertenti, che riportiamo in Figura 6.
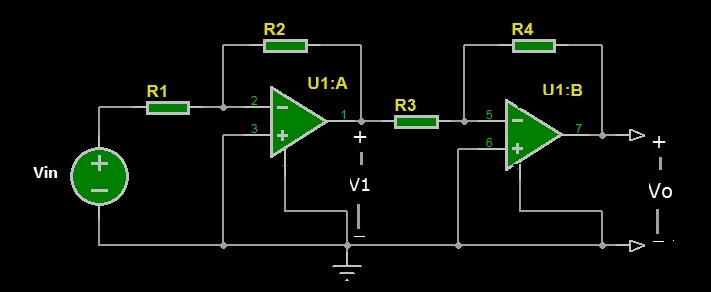
Figura 6: Schema di un circuito costituito da due amplificatori operazionali invertenti in cascata
Nel primo stadio del circuito è applicato in ingresso un generatore di tensione Vin, mentre in uscita è presente una tensione V1. Come abbiamo spiegato nelle precedenti puntate, ricordiamo che la tensione di uscita di un amplificatore invertente in configurazione base si ottiene dalla seguente formula:
Vo=-Vin*R2/R1
Ma essendo per il primo stadio V1 la tensione di uscita, riscriviamo la formula:
V1=-Vin*R2/R1
Inoltre, l’uscita del primo stadio “vede” la resistenza d’ingresso dello stadio invertente successivo, ovvero la resistenza equivalente R3. La resistenza R3 rappresenta il carico applicato ai terminali di uscita del primo stadio che, come ricordiamo dalle precedenti puntate, non produce effetti sulla tensione di uscita V1. Anche il secondo stadio si comporta esattamente come il primo, quindi la tensione di uscita si calcola con la stessa formula, ma, questa volta, la tensione applicata all’ingresso di questo secondo stadio è proprio la tensione di uscita V1 del primo, quindi avremo la seguente formula per ricavare Vo:
Vo=-V1 *R4/R3
Ora, ricaviamo l’amplificazione di tensione del primo stadio:
Av1=V1/Vin==-R4/R3
Poi l’amplificazione di tensione del secondo stadio:
Av2=Vo/V1==-R4/R3
La formula finale per calcolare la tensione di uscita Vo del circuito a due stadi operazionali invertenti in cascata, la otteniamo sostituendo V1=-Vin*R2/R1 nella formula stessa di Vo:
Vo=-(-Vin*R2/R1)*R4/R3
Svolgendo le parentesi otteniamo la formula definitiva di Vo:
Vo=Vin*(R2/R1)*(R4/R3)
Possiamo notare che la tensione di uscita Vo non è invertita di segno rispetto alla tensione d’ingresso Vin. Ciò è dovuto alla doppia inversione di segno della tensione Vin causata dall’effetto dell’inversione consecutiva effettuata dai due operazionali invertenti.
Dall’ultima formula di Vo calcoliamo l’amplificazione di tensione del circuito a due stadi operazionali:
Av=Vo/Vin=(R2/R1)*(R4/R3)
Osserviamo che l’amplificazione Av è esattamente data dal prodotto di Av1*Av2.
Esercitazione 3 - Calcolo della tensione di uscita di un circuito con due amplificatori operazionali in cascata
In questa esercitazione vogliamo calcolare la tensione di uscita e l’amplificazione di tensione del circuito mostrato in Figura 7 costituito da due stadi amplificatori operazionali in cascata.
ATTENZIONE: quello che hai appena letto è solo un estratto, l'Articolo Tecnico completo è composto da ben 3432 parole ed è riservato agli ABBONATI. Con l'Abbonamento avrai anche accesso a tutti gli altri Articoli Tecnici che potrai leggere in formato PDF per un anno. ABBONATI ORA, è semplice e sicuro.